8 Types of Math Problems for 4th Graders (2025 Guide)

The transition to fourth-grade mathematics marks a significant step, introducing multi-digit operations, fractions, and complex word problems that establish a critical foundation for all future learning. This guide is designed to break down the core math problems for 4th graders, providing a structured approach not just to find the answers, but to truly understand the "why" behind each method. We will explore eight essential problem types, from multi-digit multiplication to geometry, each presented with specific examples, strategic analysis, and actionable tips for parents, tutors, and educators. Our primary goal is to transform math practice from a daunting chore into a confident and empowering step toward mathematical fluency.

This curated collection offers a practical toolkit for mastering key concepts. You will find everything from mastering the steps of long division to visualizing the properties of angles and shapes. For learners who benefit from different teaching styles, supplementing these worksheets and practice sessions can be highly effective. For instance, understanding how to create educational videos that engage students can offer a dynamic way to demonstrate problem-solving strategies visually. This guide provides the problems and strategies that will help define your student's success this year. Let's dive in.

1. Multi-Digit Multiplication Problems

Fourth grade marks a major leap in arithmetic as students move from single-digit multiplication facts to tackling multi-digit multiplication. These math problems for 4th graders require students to multiply numbers with two or more digits, such as 23 × 45 or 156 × 7. This skill is foundational for almost all future math, including algebra and geometry, as it builds a deep understanding of place value and procedural fluency.

Problem Example & Solution

Problem: A school is buying 12 new tablets for its computer lab. If each tablet costs $158, what is the total cost?

Solution Breakdown:

1. Set up the problem: Write the multiplication problem vertically, aligning the numbers by place value.
   158
   x 12

2. Multiply by the ones digit (2):
   • 2 × 8 = 16 (Write down 6, carry over 1)
   • 2 × 5 = 10, plus the carried-over 1 = 11 (Write down 1, carry over 1)
   • 2 × 1 = 2, plus the carried-over 1 = 3 (Write down 3)
   • This gives you the first partial product: 316
3. Multiply by the tens digit (1):
   • Place a 0 in the ones place as a placeholder.
   • 1 × 8 = 8
   • 1 × 5 = 5
   • 1 × 1 = 1
   • This gives you the second partial product: 1580
4. Add the partial products:
   • 316 + 1580 = 1896

The total cost for the tablets is $1,896.

Why This Skill is Essential

Mastering multi-digit multiplication is crucial because it reinforces place value concepts and develops systematic problem-solving skills. It is a gateway to more complex topics like division, fractions with large numbers, and calculating area.

Strategic Tip: Before solving, encourage students to estimate the answer (e.g., 10 × 160 = 1600). This builds number sense and helps them check if their final answer is reasonable. Using an area model (or box method) can also provide a visual representation, making the concept of partial products much clearer.

2. Long Division Problems

Alongside multiplication, fourth grade is the year students dive deep into long division. These math problems for 4th graders involve dividing three or four-digit numbers (dividends) by one or two-digit numbers (divisors). This skill requires a solid grasp of multiplication, subtraction, and estimation, teaching students a systematic algorithm to solve complex division problems, including those with remainders.

Problem Example & Solution

Problem: A farmer harvested 1,348 apples. He wants to pack them into bags with 12 apples in each bag. How many full bags can he make, and how many apples will be left over?

Solution Breakdown:

1. Set up the problem: Write the division problem using the long division bracket.

   ---

   12 | 1348
2. Divide, Multiply, Subtract, Bring Down (DMSB):
   • Divide: How many times does 12 go into 13? It goes in 1 time. Place the 1 above the 3.
   • Multiply: 1 × 12 = 12. Write 12 below 13.
   • Subtract: 13 - 12 = 1.
   • Bring Down: Bring down the next digit, 4, to make 14.
3. Repeat the DMSB cycle:
   • Divide: How many times does 12 go into 14? It goes in 1 time. Place the 1 above the 4.
   • Multiply: 1 × 12 = 12. Write 12 below 14.
   • Subtract: 14 - 12 = 2.
   • Bring Down: Bring down the next digit, 8, to make 28.
4. Repeat the cycle again:
   • Divide: How many times does 12 go into 28? It goes in 2 times (since 12 × 2 = 24). Place the 2 above the 8.
   • Multiply: 2 × 12 = 24. Write 24 below 28.
   • Subtract: 28 - 24 = 4. There are no more digits to bring down. This is the remainder.

The farmer can make 112 full bags with 4 apples left over. For more practice, you can explore tools that solve various Long Division Problems.

Why This Skill is Essential

Long division is a critical thinking powerhouse. It teaches students to break down a large, intimidating problem into a series of manageable, repetitive steps. This procedural fluency is fundamental for understanding fractions, decimals, and ratios in later grades.

Strategic Tip: Introduce the mnemonic "Does McDonald's Sell Burgers?" (Divide, Multiply, Subtract, Bring Down) to help students remember the steps. Also, encourage them to check their work by multiplying the quotient by the divisor and adding the remainder (112 × 12 + 4 = 1348).

3. Fraction Problems with Like Denominators

Fourth grade is a crucial year for introducing fractions, moving them from abstract concepts to concrete numbers that can be manipulated. These math problems for 4th graders focus on adding and subtracting fractions that share the same denominator (e.g., 3/8 + 2/8). This foundational skill teaches students that fractions represent parts of a whole and sets the stage for future work with unlike denominators, mixed numbers, and multiplying fractions.

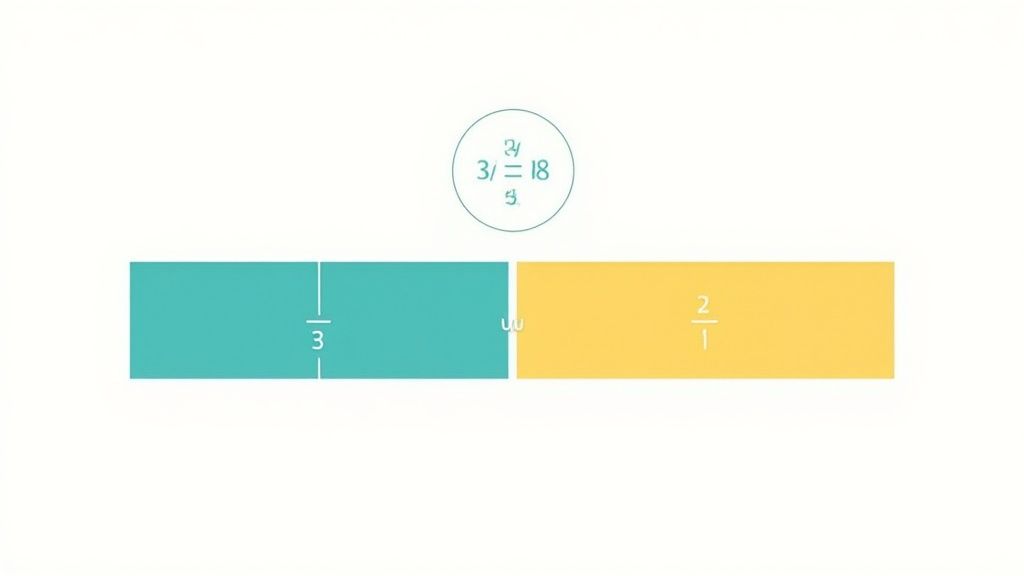
Problem Example & Solution

Problem: Maria is baking a cake. The recipe calls for 3/8 of a cup of sugar for the batter and 2/8 of a cup of sugar for the frosting. How much sugar does she need in total?

Solution Breakdown:

1. Identify the operation: The problem asks for the "total" amount, which means we need to add the two fractions.
   • 3/8 + 2/8 = ?
2. Add the numerators: The numerators are the top numbers of the fractions. We add them together.
   • 3 + 2 = 5
3. Keep the denominator the same: When adding fractions with like denominators, the denominator (the bottom number) does not change. It still represents the size of the equal parts of the whole.
   • The denominator remains 8.
4. Combine to form the answer: Place the sum of the numerators over the original denominator.
   • The result is 5/8.

Maria needs a total of 5/8 of a cup of sugar.

Why This Skill is Essential

Understanding how to add and subtract fractions with like denominators is the first major step into fractional arithmetic. It reinforces the concept of a fraction as a number and demonstrates that basic operations (addition, subtraction) apply to fractions just as they do to whole numbers. This skill is vital for understanding measurement, data analysis, and more advanced mathematical concepts.

Strategic Tip: Use visual aids like fraction bars, circles, or even a drawn pizza. This helps students see why the denominator stays the same. For example, if you add 3 slices of a pizza cut into 8 pieces to 2 more slices from the same pizza, you have 5 slices, but they are still eighths. This visual connection is key to building conceptual understanding.

4. Decimal Place Value and Comparison Problems

In fourth grade, students begin to explore numbers that are not whole. These math problems for 4th graders introduce decimals, connecting the familiar concept of place value to the new world of tenths and hundredths. This skill involves identifying, reading, writing, and comparing decimal numbers, which is crucial for understanding concepts like money and measurement.

Problem Example & Solution

Problem: Sarah ran 2.65 miles on Monday. On Tuesday, she ran 2.8 miles. On which day did she run farther?

Solution Breakdown:

1. Set up the problem: Write the two decimal numbers, aligning them by the decimal point. If one number has fewer decimal places, add a zero as a placeholder.
   2.65
   2.80 (Adding a zero helps with direct comparison)
2. Compare the whole number part: Both numbers have a "2" in the ones place, so they are equal so far. Move to the next place value to the right.
3. Compare the tenths place:
   • The first number has a "6" in the tenths place (0.6).
   • The second number has an "8" in the tenths place (0.8).
4. Determine the larger number:
   • Since 8 is greater than 6, the number 2.80 is greater than 2.65.

Sarah ran farther on Tuesday.

Why This Skill is Essential

Understanding decimal place value is a fundamental bridge between whole numbers and fractions. It is essential for everyday tasks such as handling money, interpreting measurements, and reading data. Mastering this skill prevents future confusion with more complex mathematical operations involving decimals and percentages. For effective learning, it's key to know how to study math effectively, especially with new concepts like this.

Strategic Tip: Use a place value chart to visually organize the digits of each decimal. Comparing decimals is similar to comparing words alphabetically: you start from the left and find the first place where the digits differ. Using money (e.g., $2.65 vs. $2.80) is an excellent real-world analogy that makes the concept instantly relatable for students.

5. Multi-Step Word Problems with Mixed Operations

Fourth grade is a pivotal time when students transition from single-step problems to more complex scenarios requiring multiple calculations. These multi-step math problems for 4th graders challenge students to use addition, subtraction, multiplication, and division in the correct sequence to find a solution. This skill is vital for developing critical thinking, logical reasoning, and real-world problem-solving abilities.

Problem Example & Solution

Problem: The school library has 1,128 books. On Monday, students checked out 174 books. On Tuesday, the librarian received a new shipment of 5 boxes, with 24 books in each box. How many books does the library have now?

Solution Breakdown:

1. Step 1: Find the total number of new books.
   • The librarian received 5 boxes with 24 books each. This is a multiplication problem.
   • 5 × 24 = 120
   • The library received 120 new books.
2. Step 2: Find the number of books after Monday's check-outs.
   • The library started with 1,128 books and 174 were checked out. This is a subtraction problem.
   • 1,128 - 174 = 954
   • The library had 954 books left on Monday evening.
3. Step 3: Add the new books to the current total.
   • The library had 954 books, and 120 new books were added. This is an addition problem.
   • 954 + 120 = 1074

The library now has a total of 1,074 books.

Why This Skill is Essential

Solving multi-step word problems builds crucial executive functioning skills, such as planning, sequencing, and self-monitoring. It teaches students to decode complex information and break it down into manageable parts. This lays the groundwork for tackling advanced mathematical and scientific challenges where multiple steps and operations are the norm. For a deeper look, you can learn more about how to solve math problems step-by-step.

Strategic Tip: Encourage students to use strategies like CUBES (Circle numbers, Underline the question, Box key words, Eliminate extra info, Solve). Drawing a simple diagram or picture can also help them visualize the problem's sequence and decide which operation to perform first.

6. Area and Perimeter Problems

In fourth grade, students dive into practical geometry by learning to calculate the area and perimeter of two-dimensional shapes, primarily rectangles. These math problems for 4th graders are highly relatable as they connect multiplication and addition to real-world scenarios like fencing a yard or carpeting a room. Understanding the difference between area (the space inside a shape) and perimeter (the distance around a shape) is a critical geometric concept.

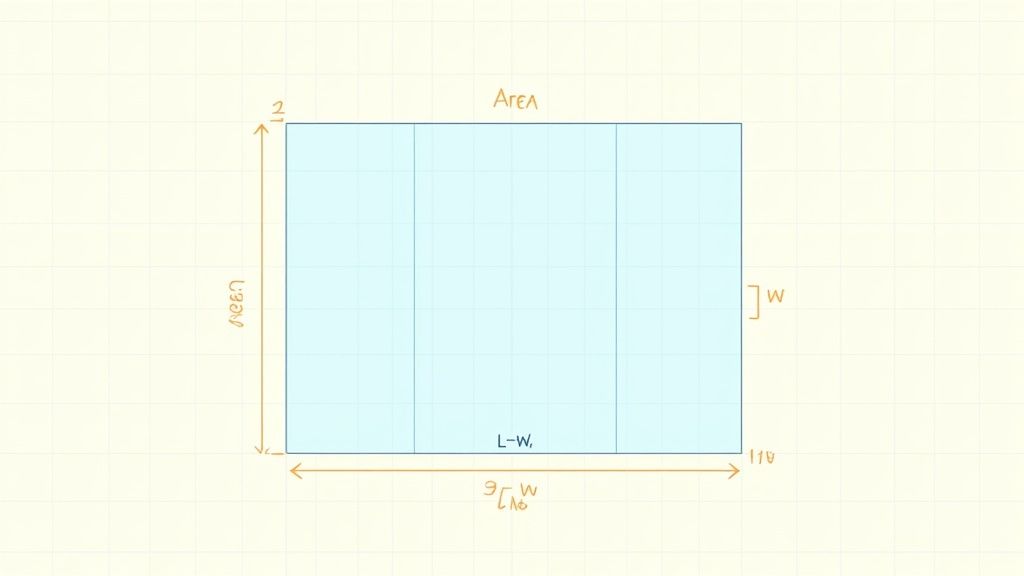
Problem Example & Solution

Problem: A rectangular community garden is 9 meters long and 7 meters wide. What is the perimeter of the garden, and what is its total area?

Solution Breakdown:

1. Calculate the Perimeter: The perimeter is the sum of all the side lengths. For a rectangle, the formula is P = 2 × (length + width).

   • Add the length and width: 9 m + 7 m = 16 m
   • Multiply the sum by 2: 16 m × 2 = 32 meters
   • Alternatively, add all four sides: 9 + 7 + 9 + 7 = 32 meters.

2. Calculate the Area: The area is the space inside the shape. The formula for the area of a rectangle is A = length × width.

   • Multiply the length by the width: 9 m × 7 m = 63 square meters

The garden has a perimeter of 32 meters and an area of 63 square meters.

Why This Skill is Essential

Calculating area and perimeter is a student's first step into applying mathematical formulas to solve spatial problems. It strengthens their multiplication skills and introduces the concept of units and square units, which is fundamental for later studies in geometry, physics, and even design. These problems teach students to distinguish between different types of measurements for the same object.

Strategic Tip: Use grid paper to visually represent area by having students count the squares inside a drawn rectangle. To teach perimeter, have them trace the outline with a colored pencil. This hands-on approach helps solidify the abstract difference between the two concepts and prevents common mix-ups.

7. Estimation and Rounding Problems

Estimation and rounding are practical skills that build a student's number sense and ability to make quick, logical judgments about quantities. These math problems for 4th graders challenge students to round numbers to a specific place value (like the nearest ten, hundred, or thousand) and use those rounded numbers to find an approximate answer. This skill is incredibly useful in everyday life, from estimating a grocery bill to planning party supplies.

Problem Example & Solution

Problem: A theme park sold 3,824 tickets on Friday, 5,147 tickets on Saturday, and 4,591 tickets on Sunday. About how many tickets were sold in total over the weekend? (Estimate by rounding each number to the nearest hundred).

Solution Breakdown:

1. Identify the goal: The question asks for an "about how many" total, which signals the need for estimation, not an exact calculation.
2. Round each number to the nearest hundred:
   • 3,824: Look at the tens digit (2). Since 2 is less than 5, the hundreds digit (8) stays the same. So, 3,824 rounds to 3,800.
   • 5,147: Look at the tens digit (4). Since 4 is less than 5, the hundreds digit (1) stays the same. So, 5,147 rounds to 5,100.
   • 4,591: Look at the tens digit (9). Since 9 is 5 or greater, we round up the hundreds digit (5) to 6. So, 4,591 rounds to 4,600.
3. Add the rounded numbers:
   • Set up the addition problem with the rounded values.
     3800
     5100
   • 4600

   ---

   13500
   The theme park sold about 13,500 tickets over the weekend.

Why This Skill is Essential

Estimation is a powerful mental math tool that helps students check the reasonableness of their answers. Before tackling a complex multi-step problem, a quick estimate provides a benchmark. If the final calculated answer is far from the estimate, it signals a potential error. This skill develops critical thinking and makes math more intuitive and applicable to the real world.

Strategic Tip: Use a number line to visually teach rounding. Mark the two "benchmark" hundreds (e.g., 3800 and 3900 for rounding 3824) and show students which one the number is closer to. This visual aid makes the abstract "rounding rule" much more concrete and easier to understand.

8. Angle Measurement and Geometric Properties Problems

In fourth grade, geometry expands from simply identifying shapes to analyzing their specific attributes. These math problems for 4th graders focus on measuring angles with a protractor, classifying shapes based on properties like parallel lines and angle types, and understanding concepts like symmetry. This shift introduces students to more formal geometric reasoning, which is essential for future success in math and science.

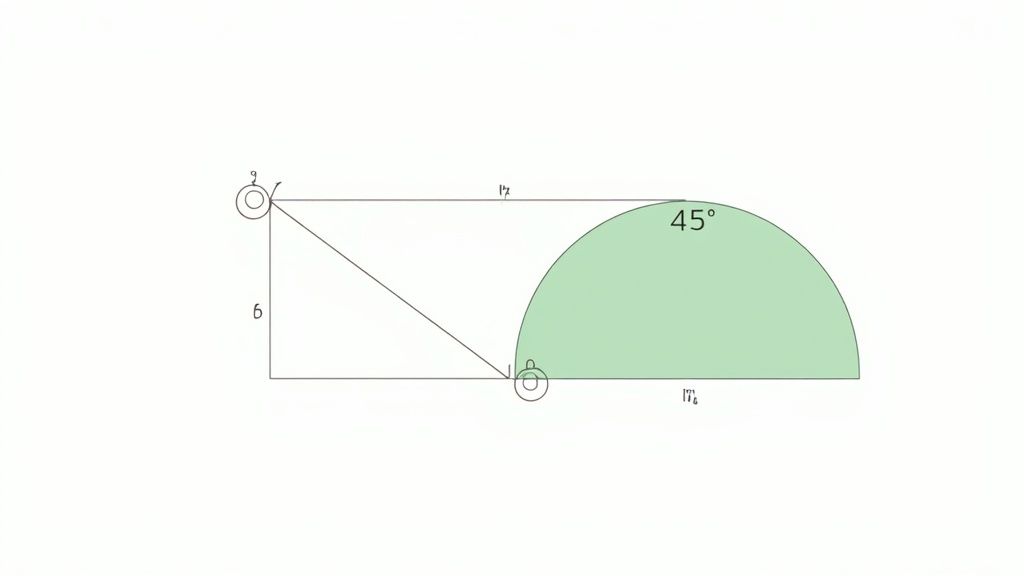
Problem Example & Solution

Problem: Look at the shape below. Identify the types of angles present (acute, right, obtuse) and determine if the shape has any lines of symmetry.

Solution Breakdown:

1. Analyze the shape's angles: First, identify the vertices (corners) where angles are formed.
   • The bottom-left corner is a perfect square corner, which indicates a right angle (exactly 90°).
   • The top angle is smaller than a right angle, making it an acute angle (less than 90°).
   • The bottom-right angle is also smaller than a right angle, making it another acute angle.
2. Identify lines of symmetry: A line of symmetry is a line that divides a shape into two identical, mirror-image halves.
   • Imagine folding the triangle vertically down the middle. The two sides would not match up perfectly.
   • Imagine folding it horizontally. The top and bottom halves would not match.
   • Imagine folding it diagonally. The halves would not align.
3. State the conclusion: The triangle has one right angle and two acute angles. It is a right triangle. It has zero lines of symmetry.

Why This Skill is Essential

Understanding geometric properties and angle measurement develops spatial reasoning and logical thinking. These skills are not just for geometry class; they are applied in fields like art, architecture, and engineering. Learning to classify and analyze shapes helps students recognize patterns and organize information systematically.

Strategic Tip: Introduce angles by relating them to the hands on a clock. A quarter turn (like 3 o'clock) is a 90° right angle. Anything smaller is acute, and anything larger is obtuse. For hands-on practice, have students use their arms to form different angles or find examples of them in the classroom.

4th Grade Math: 8-Topic Comparison

Topic	Implementation complexity	Resource requirements	Expected outcomes	Ideal use cases	Key advantages
Multi-Digit Multiplication Problems	Moderate — multi-step algorithm and place-value work	Minimal — paper, pencil, area models or manipulatives optional	Improved computational fluency; readiness for algebraic work	Calculating totals, area, bulk quantities	Builds fluency; connects concrete models to standard algorithm
Long Division Problems	High — multi-step algorithm with estimation and remainders	Moderate — guided examples, manipulatives, scaffolded practice	Systematic problem solving; understanding of division and remainders	Sharing/grouping scenarios, conversions, fraction foundations	Reinforces operations; essential for later fraction concepts
Fraction Problems with Like Denominators	Low — straightforward add/subtract of numerators	Visual aids recommended — fraction bars, circles, models	Foundational fractional reasoning; precursor to unlike denominators	Combining parts in recipes, time, distance problems	Clear algorithm; strong visual representations
Decimal Place Value and Comparison Problems	Low–Moderate — place-value focus and ordering	Place-value charts, base-ten blocks, money models, number lines	Decimal literacy; accurate reading/comparing of measurements and money	Price comparisons, measurements, data recording	Direct link to money/measurement; concrete visual supports
Multi-Step Word Problems with Mixed Operations	High — requires interpretation and strategy selection	Scaffolds, diagrams, explicit problem-solving strategies	Enhanced reasoning, decision-making, math reading comprehension	Real-world planning, budgeting, multi-step tasks	Develops higher-order problem solving; models authentic math use
Area and Perimeter Problems	Moderate — apply formulas and combine shapes for composites	Grid paper, rulers, manipulatives, measurement tools	Spatial reasoning; apply multiplication/addition to geometry	Floor planning, fencing, design and measurement tasks	Concrete visual application of multiplication; practical relevance
Estimation and Rounding Problems	Low — rules-based but requires judgment	Number lines, anchor charts, contextual examples	Strong number sense; fast mental math and reasonableness checks	Quick budgeting, approximation before calculation, checks for answers	Improves mental computation and sense-making; practical everyday use
Angle Measurement and Geometric Properties Problems	Moderate–High — protractor use and classification skills	Protractors, geometry tools, dynamic geometry software	Measurement accuracy; geometric vocabulary and classification	Geometry tasks, design, art and architecture contexts	Hands-on measurement skills; supports spatial and design thinking

Key Takeaways for Building 4th Grade Math Mastery

Navigating the landscape of fourth-grade mathematics is a pivotal journey for young learners. The transition from basic arithmetic to more complex, multi-step thinking marks a significant leap in their academic development. The collection of math problems for 4th graders detailed in this guide—from multi-digit multiplication and long division to fractions, decimals, and geometry—serves as a comprehensive roadmap for building a solid foundation.

Mastery isn't just about memorizing formulas; it's about developing a deep, conceptual understanding. The most effective approach combines consistent practice with a focus on the logic behind the methods. When a student can explain why they carry a one in addition or why a common denominator is needed, they are building true mathematical fluency.

Strategic Pillars for Success

To truly empower your fourth grader, focus on these core strategic pillars derived from the problems we've explored:

• Visualize the Concept: For abstract topics like fractions or area, visual aids are non-negotiable. Encourage drawing models, using manipulatives, or finding digital tools that represent the numbers. This transforms abstract ideas into tangible, understandable concepts.
• Deconstruct Word Problems: The biggest hurdle in word problems is often not the math but the language. Teach students to break them down systematically: identify the knowns, pinpoint the unknown, and highlight the key operational words (e.g., "total," "left," "each").
• Connect Math to the Real World: Context is king. Frame problems in relatable scenarios. Calculating the perimeter for a garden, dividing snacks among friends, or comparing prices using decimals makes the math meaningful and less intimidating.
• Embrace Productive Struggle: It is crucial to allow students time to wrestle with a problem before jumping in to help. This process builds resilience and critical-thinking skills. When they do get stuck, guide them with questions rather than giving them the answer directly.

Key Insight: The goal is not just to find the correct answer but to understand the process and build the confidence to tackle unfamiliar math problems for 4th graders in the future. Each mistake is a learning opportunity, a clue to where a concept needs reinforcement.

Actionable Next Steps for Lasting Impact

Moving forward, the path to mastery is paved with consistent, targeted effort. Use the downloadable worksheets provided throughout this article to establish a regular practice routine. Start with the easier problems to build confidence and gradually introduce more complex challenges.

Celebrate progress, not just perfection. Acknowledge the effort and persistence your student shows, as this fosters a positive mindset toward mathematics. As they become more comfortable with the core topics of multiplication, division, fractions, and geometry, they will be well-equipped for the more advanced concepts that await them in fifth grade and beyond. By focusing on these strategies, you are not just helping them solve a worksheet; you are nurturing a capable, confident, and analytical thinker.

---

Stuck on a tricky problem or need an instant explanation for a tough concept? Feen AI acts as a 24/7 personal tutor, providing step-by-step guidance for the exact math problems for 4th graders you're working on. Get unstuck and build confidence by trying Feen AI today.