How to solve calculus problems: A Practical Guide

If you’re trying to solve calculus problems by just memorizing formulas, you're making it much harder than it needs to be. Real success in calculus comes from having a rock-solid foundation in the math that comes before it, especially algebra and trigonometry. Think of these skills as your toolkit—they're what you'll use to actually do the calculus. A strong base turns what looks like an impossible problem into a puzzle you know how to solve.

Build a Strong Calculus Foundation

Getting good at calculus feels less like learning a new language and more like using familiar tools in clever new ways. From my experience, the most common reason students get stuck isn't the calculus itself—it's the algebra, geometry, or trig hiding inside the problem. When you stumble trying to factor a polynomial or can't remember a key trig identity, your brain has to switch gears. You stop thinking about the calculus and start wrestling with the basics.

This is a surprisingly common problem. Many students jump into calculus without being fully prepared. For example, in the United States, around 80% of high school students take calculus primarily to beef up their college applications, not because they've truly mastered the prerequisites. The result? A shocking 80% of them end up retaking calculus in college. This shows that their first pass wasn't enough for the demands of higher-level math.

Here's a good rule of thumb: if you can't explain how you solved a problem to a classmate in a way they understand, you probably don't fully understand it yourself.

This disconnect tells a critical story: you can't build a skyscraper on a flimsy foundation. Trying to solve calculus problems without being fluent in algebra is like trying to write a novel without a firm grasp of grammar. You might get some words on the page, but it's going to be a slow, painful process filled with errors.

Pinpointing Your Foundational Gaps

So, how do you make sure your foundation is solid? It starts with an honest look at your skills. Don't just assume you remember everything from your past math classes. You need to actively test yourself in these core areas:

• Algebraic Manipulation: How quickly can you factor polynomials, simplify messy fractions, or handle rational expressions? In calculus, you'll be doing this constantly.
• Functions and Their Properties: Are you genuinely comfortable with function notation, finding the domain and range, and understanding transformations? This is the language of calculus.
• Trigonometry: Is the unit circle your friend? Can you recall key trigonometric identities and visualize the graphs of sine, cosine, and tangent? These are non-negotiable for problems involving anything circular or periodic.
• Logarithmic and Exponential Rules: Can you confidently apply the rules of logs and exponents? They are vital for derivatives and integrals related to growth and decay.

If you feel even a little shaky in any of these areas, that’s your sign to hit pause and review. Spending a few hours sharpening these skills now will save you dozens of hours of frustration down the road. For some great strategies, check out our guide on https://feen.ai/blog/how-to-study-math-effectively.

This table breaks down exactly why these pre-calculus concepts are so essential.

Key Foundational Concepts for Calculus Success

Pre-Calculus Concept	Why It's Critical for Calculus	Example Application
Factoring Polynomials	Essential for finding limits, critical points, and roots of derivatives.	To find where a function's slope is zero, you set the derivative equal to zero and solve—which often requires factoring.
Trigonometric Identities	Simplifies complex integrands and derivatives involving trig functions.	Using sin²x + cos²x = 1 can turn an impossible-looking integral into a simple one.
Logarithm Properties	Crucial for logarithmic differentiation and solving exponential models.	Applying ln(a/b) = ln(a) - ln(b) can simplify complex functions before taking the derivative.
Function Transformations	Helps you visualize and understand the behavior of functions and their derivatives.	Knowing how f(x-c) shifts a graph helps you predict how its derivative will behave.

By mastering these fundamentals, you set yourself up for genuine understanding, not just rote memorization.

Moving from Memorization to Mastery

The goal is to understand why the rules work, not just what they are. When you get the "why," you can apply your knowledge to problems you've never seen before. That's the difference between just surviving calculus and actually excelling at it.

Beyond the math concepts, you also need solid study habits. Building consistency is key, so it might be helpful to explore some actionable self-discipline techniques. When you invest time in your pre-calculus knowledge, you’re not taking a detour—you’re building an expressway to solving calculus problems with confidence. This prep work allows you to focus your mental energy on the new, exciting ideas in calculus instead of getting bogged down by old mechanics.

Don't Just Stare at It—Have a Game Plan

We've all been there. You're staring at a beast of a calculus problem, and your mind just goes blank. Hoping the solution will just pop into your head is a fast track to frustration. The secret isn't knowing every single trick, but having a consistent game plan—a mental roadmap that takes you from "I have no idea" to "Okay, I see the path."

This isn't about some rigid, one-size-fits-all formula. It’s a flexible process that stops you from making wild guesses and encourages deliberate, confident problem-solving. It forces you to slow down and actually think before you start crunching numbers, which is where most of those silly mistakes happen.

The Four Pillars of Smart Problem-Solving

An effective framework really boils down to four key stages. Think of it less like a rigid checklist and more like a cycle of thinking you can apply to almost any problem that comes your way.

1. Figure Out What’s Really Being Asked: First, read the question. Then, read it again. Seriously. Pinpoint exactly what you’re given and what you’re supposed to find. For problems involving shapes or motion—like optimization or related rates—sketching a quick diagram is a game-changer. It helps you see the moving parts.

2. Map Out Your Attack: Before you write a single equation, think strategy. What calculus concepts or theorems feel relevant here? Is it a limit that’s screaming for L'Hôpital's Rule? An integral that looks like a perfect candidate for u-substitution? This plan is your bridge from the knowns to the unknown.

3. Do the Math (Carefully): Now it’s time to execute. Follow the steps you just laid out, keeping your work neat and logical. Showing your work clearly isn't just for your professor; it's for you. It helps you stay organized and makes it way easier to backtrack and find a mistake if the final answer feels weird.

4. Do a Sanity Check: You got an answer. Don't just circle it and move on. Step back and ask: does this actually make sense? If you were asked to find the maximum area of a field and got a negative number, something’s obviously gone wrong. Reread the prompt one last time to make sure you answered the actual question.

This isn't just a technique for passing tests. Research in math education consistently shows that strong problem-solving comes from developing higher-order thinking. That means going beyond plug-and-chug calculations to actively analyzing and evaluating the problem itself. A great study on integral calculus problem-solving digs deeper into this pedagogical approach, confirming that a structured process promotes a much deeper engagement with the material.

Putting the Framework into Action

Let's walk through how this works with a classic optimization problem.

Problem: You have 100 feet of fencing to build a rectangular garden. What is the largest possible area you can enclose?

• Understand the Problem:

  • What I have (Givens): A total of 100 feet of fence, which is the perimeter. The shape is a rectangle.
  • What I need (Goal): The maximum possible area. I'll use L for length and W for width.

• Devise a Plan:

  • I have two key formulas: Perimeter = 2L + 2W and Area = L * W.
  • I need to maximize the area, A. To do that with calculus, I first need an area formula with just one variable.
  • My plan is to use the perimeter equation (2L + 2W = 100) to express L in terms of W. Then I can substitute that into the area formula.
  • Once I have A(W), I'll take the derivative, A'(W), set it to zero, and solve. That will give me the width that creates the maximum area.

• Execute the Plan:

  1. Start with the perimeter: 2L + 2W = 100. I can simplify this to L + W = 50, which means L = 50 - W.
  2. Now, substitute this into the area formula: A = (50 - W) * W. This gives me A(W) = 50W - W².
  3. Time for the derivative: A'(W) = 50 - 2W.
  4. Find the critical point by setting the derivative to zero: 50 - 2W = 0.
  5. Solving for W gives 2W = 50, so W = 25 feet.
  6. If W = 25, then L = 50 - 25, so L = 25 feet.
  7. The maximum area is A = 25 * 25 = **625 square feet**.

• Look Back and Reflect:

  • Does this check out? A 25x25 garden is a square. Its perimeter would be 2(25) + 2(25) = 100 feet. That matches the given info.
  • Intuitively, a square feels like the most efficient way to maximize area for a given perimeter, so the answer feels right. It passes the sanity check.

This structured thinking is a powerhouse tool that works for way more than just optimization problems. To see it applied more broadly, check out our guide on how to solve math problems step-by-step. The more you use a consistent framework, the more your brain starts to recognize patterns on its own, making you a much faster and more accurate problem-solver.

Mastering Limits, Derivatives, and Integrals

Alright, we've covered the high-level strategies. Now it’s time to get our hands dirty with the "big three" of calculus: limits, derivatives, and integrals. These are the gears that make the entire machine work. If you can build a solid intuition for how to tackle these, you're well on your way to solving almost any calculus problem thrown at you.

Think of it like learning to cook. You can read all the theory about heat and flavor chemistry, but you only get good by actually chopping vegetables and working the stove. This is where we start cooking.

This simple workflow is a great mental model to have when you're staring down a new problem. It’s a reminder to slow down, understand what's being asked, and make a plan before jumping into the calculations.

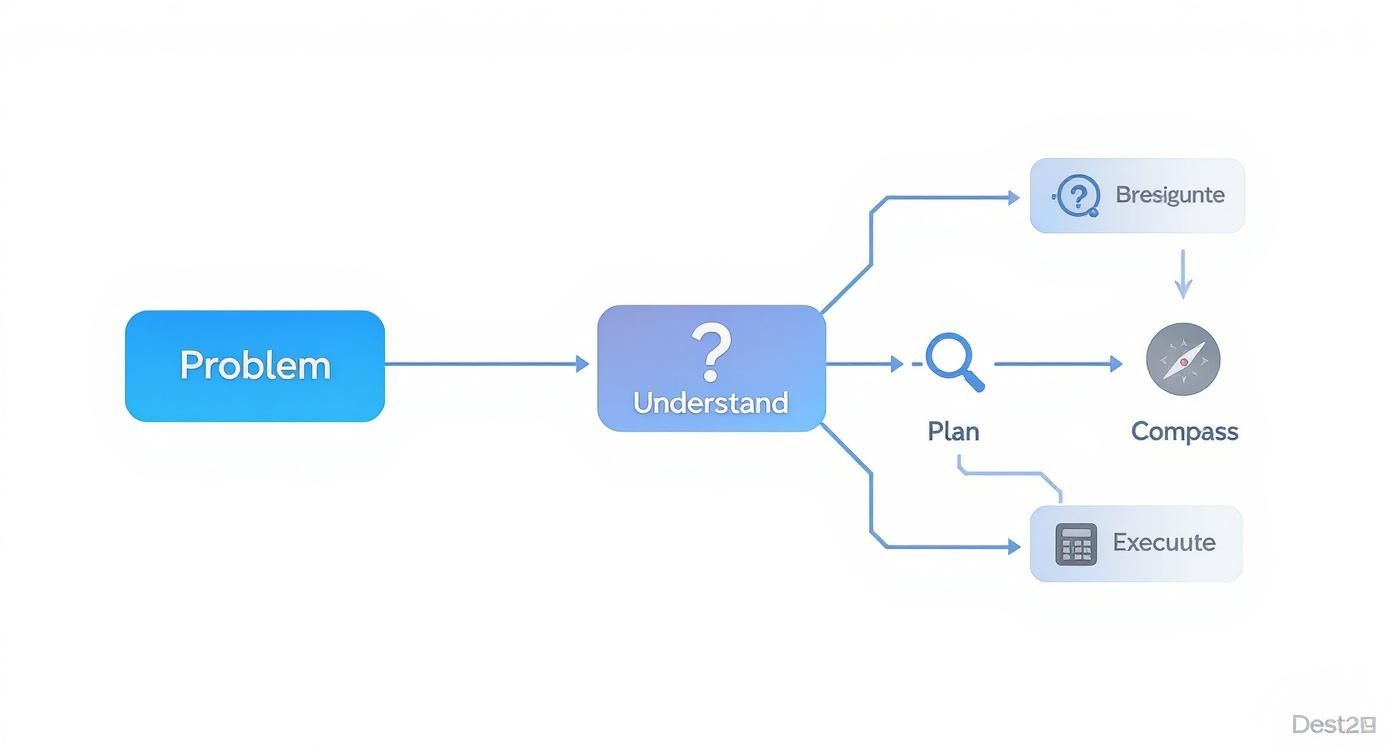
As the diagram shows, a solid solution is built on a foundation of understanding, not just number-crunching.

Conquering Limits and Indeterminate Forms

Limits are the bedrock of calculus—they’re what derivatives and integrals are built upon. Many are simple enough to solve by just plugging in the number. But the real challenge comes when you hit an indeterminate form, like 0/0 or ∞/∞.

When direct substitution gives you one of these, don't panic. It's just a signal that you need to bring out a more specialized tool. One of the most powerful is L'Hôpital's Rule. This neat trick lets you take the derivative of the top and bottom of the fraction separately, then try the limit again.

Pro Tip: Remember, L'Hôpital's Rule is only for 0/0 and ∞/∞ forms. A super common mistake is to apply it to something like 1/0. Always check the form first, or you'll get a nonsensical answer.

Let's walk through one.

• Problem: Find the limit of (e^x - 1) / x as x approaches 0.
• Initial Check: Plugging in x = 0 gives us (e^0 - 1) / 0, which is (1 - 1) / 0, or 0/0. That's our green light for L'Hôpital's.
• Execution:
  • The derivative of the numerator (e^x - 1) is just e^x.
  • The derivative of the denominator (x) is 1.
• Re-evaluate: Now we find the limit of e^x / 1 as x approaches 0. Plugging in 0 gives e^0 / 1, which is just 1.

Don’t forget about good old-fashioned algebra, either. Sometimes, simply factoring, canceling terms, or multiplying by the conjugate can clear up the indeterminate form without needing any derivatives at all.

Demystifying Derivatives with Key Rules

Derivatives are all about measuring instantaneous rates of change. You probably have the power rule down, but the real art is knowing when to deploy the product, quotient, and chain rules for more tangled functions.

• Product Rule: Use this when you're differentiating two functions multiplied together, like f(x) * g(x). A classic case is x² * sin(x).
• Quotient Rule: This is your go-to for a fraction of two functions, like f(x) / g(x). Think of something like (2x + 1) / (x² - 3).
• Chain Rule: This is the big one. You'll use it constantly. It's for nested functions—a function inside of another function, written as f(g(x)). A perfect example is sin(x³), where the x³ function is tucked inside the sin(x) function.

Let's break down a Chain Rule problem.

Problem: Find the derivative of h(x) = (x² + 5x)^4.

1. Identify the Functions: The "outer" function is u⁴, and the "inner" function is u = x² + 5x.
2. Differentiate the Outer: The derivative of u⁴ is 4u³.
3. Differentiate the Inner: The derivative of x² + 5x is 2x + 5.
4. Multiply and Substitute: The chain rule says to multiply these two results. That gives us 4u³ * (2x + 5). Now, just pop the original inner function back in for u: 4(x² + 5x)³ * (2x + 5).

Spotting which rule to use becomes second nature with practice. Many problems will even require you to combine them, like using the quotient rule where the numerator requires the chain rule.

Unlocking Integrals: Indefinite and Definite

Integration is essentially the reverse of differentiation—it’s about finding the area under a curve. You'll deal with two main flavors.

• Indefinite Integrals: These find the general antiderivative and always end with + C, the constant of integration. For instance, the indefinite integral of 2x is x² + C.
• Definite Integrals: These calculate a specific number that represents the area between two points, a and b. You don't need the + C here because it always cancels out when you evaluate.

For anything more complex than a basic function, you'll need some advanced techniques in your toolkit.

Key Integration Techniques

Technique	When to Use It	Example Problem
U-Substitution	When you see a function and its derivative (or a multiple of it) in the integral. It's the chain rule in reverse.	∫ 2x * cos(x²) dx (Let u = x²)
Integration by Parts	For integrals with products of different function types, like a polynomial and a trig function. The LIATE mnemonic helps you pick 'u'.	∫ x * e^x dx
Partial Fractions	When integrating a rational function (a polynomial fraction) where you can factor the denominator.	∫ (5x - 3) / (x² - 2x - 3) dx

Let's work through a quick u-substitution.

Problem: Evaluate the integral of ∫ (x+1) / (x² + 2x)³ dx.

1. Choose 'u': The stuff inside the parenthesis, x² + 2x, looks like a good candidate. Let u = x² + 2x.
2. Find 'du': Differentiating u gives us du = (2x + 2) dx. If we factor out a 2, we get du = 2(x + 1) dx. This is great news!
3. Substitute: Our integral has (x+1) dx. From our last step, we can solve for that: (x+1) dx = du / 2.
4. Rewrite the Integral: Now we can swap everything out. The integral becomes ∫ (1 / u³) * (du / 2). Let's pull the constant out: (1/2) ∫ u⁻³ du.
5. Integrate: This is easy. The integral of u⁻³ is u⁻² / -2. So we have (1/2) * (u⁻² / -2), which simplifies to -1/4 * u⁻².
6. Back-substitute: The final step is to replace u with what it originally was: -1 / (4(x² + 2x)²) + C.

Solving these core calculus problems isn't about memorizing a thousand different solutions. It's about recognizing patterns, knowing which tool to grab, and being methodical as you work through the steps.

Connecting Calculus to Real World Problems

Calculus isn't just a bunch of abstract rules from a textbook. Think of it as the language we use to describe a world that’s constantly in motion. Its real power clicks into place when you learn how to translate messy, real-world scenarios into clean, solvable equations. Honestly, that skill—getting from a word problem to a mathematical model—is one of the most valuable things you'll take away from any calculus course.

This is where derivatives and integrals stop being theoretical and start feeling real. You’re no longer just finding the slope of some generic curve; you're pinpointing the exact moment a company's profits hit their peak. You're not just calculating the area under a line; you're figuring out the total volume of water that flowed through a dam over a weekend.

Making that connection is everything. It's no surprise that international comparisons show a huge gap in math education based on this very idea. The 2022 PISA assessment highlighted that U.S. students scored below the international average, while students in places like Singapore and Japan, where problem-solving and hands-on learning are prioritized, came out on top.

Tackling Optimization Problems

One of the first and most practical applications you’ll run into is optimization. The goal is always the same: find the absolute best-case scenario. It’s all about using derivatives to find a maximum or a minimum value.

Picture it from a business angle. A company needs to design a soda can that holds a specific volume—say, 355 ml—but they want to use the least amount of aluminum possible to keep costs down. That's a classic optimization problem.

Here’s the breakdown:

• The Goal: Minimize the can's surface area.
• The Constraint: The volume must be exactly 355 ml.
• The Calculus: You set up a function for the surface area, use the volume constraint to boil it down to one variable (like the can's radius), and then take the derivative. Set that derivative to zero, and you can solve for the perfect dimensions.

These problems force you to build equations from the ground up, a skill that’s far more useful than just plugging numbers into a formula.

The hardest part of a word problem is almost never the calculus itself. It’s translating the words into the correct initial equations. Once you have the right function, the derivative is usually the easy part.

Unraveling Related Rates

Another fascinating area is related rates. These problems throw you into situations where multiple things are changing over time, and your job is to figure out how their rates of change are connected. This is where the chain rule truly becomes your superpower.

Think about blowing up a spherical balloon. As you inflate it, its volume and its radius are both getting bigger, but they aren't increasing at the same rate. Related rates let you answer questions like, "If the volume is increasing at 100 cm³/s, how fast is the radius expanding when the radius hits 5 cm?"

To solve it, you’d start with the volume formula for a sphere, differentiate both sides with respect to time (this is the key step!), and then plug in what you know to solve for the rate you don't. It’s an incredibly powerful way to model dynamic, moving systems.

From Words to Equations

The secret to cracking these problems is learning to decode their language. Certain keywords are direct signals for specific calculus operations. If you can spot them, you're halfway to setting up the right equation.

Translating Word Problems into Calculus Equations

Here's a quick guide to help you identify the common clues hidden in word problems and connect them to the right calculus concept.

Keyword/Phrase in Problem	Corresponding Calculus Concept	Example Clue
"Largest," "smallest," "maximum," "minimum," "most," "least"	Optimization (finding critical points of a function using derivatives)	"What is the maximum profit?"
"How fast," "rate of change," "growing," "shrinking," "velocity"	Derivatives (representing an instantaneous rate of change)	"How fast is the water level rising?"
"At what rate... when..."	Related Rates (using implicit differentiation with respect to time)	"Find the rate the shadow is lengthening when he is 10 feet from the pole."
"Total amount," "accumulation," "area," "volume"	Integration (summing up infinitesimal pieces over an interval)	"Find the total distance traveled from t=0 to t=5."

Once you start seeing these applications in action, you build an intuition for solving calculus problems that goes far beyond the classroom. You learn to see the world not just as it is, but as a system of interconnected, constantly changing parts.

Using Tools and Resources for Smart Practice

Getting good at calculus isn't about grinding through hundreds of identical problems. It’s about practicing smart. The real goal is to deepen your understanding with every single problem you solve. This mindset shifts homework from a tedious chore into a focused training session.

A solid practice strategy pulls from more than just your textbook. You need a full support system. Online problem banks give you variety, study groups offer fresh perspectives, and new digital tools can provide guidance right when you need it. The trick is knowing which resource to use and when.

Leveraging AI as a Learning Partner

An AI math solver can be an incredible learning partner, but only if you use it the right way. It’s tempting to just grab the final answer and move on, but that’s a huge missed opportunity. Think of it less like an answer key and more like a personal tutor who’s on call 24/7.

Here's how to use it to actually learn, not just get by:

• Deconstruct Tricky Steps: Stuck on one specific part, like a messy algebraic simplification or a non-obvious substitution? Ask the AI to explain just that step. This gets you past the roadblock without giving away the entire solution.
• Check Your Work Strategically: Once you’ve worked through a problem on your own, use the tool to verify your answer and your method. If you got it wrong, you can compare your steps to the AI’s solution and see exactly where things went sideways.
• Explore Alternative Paths: There’s often more than one way to solve a calculus problem. Try asking the AI for a different method. This can illuminate connections between concepts you hadn't seen before and seriously deepen your understanding.

When you use these tools as a guide instead of a crutch, you stay in the driver's seat of your own education. It’s how you turn a simple homework set into a chance to build real, lasting skills. For a great example of this in action, check out the features available on platforms like Feen AI's math solver at https://feen.ai/ai-math-solver.

The goal of practice isn't just to get the right answer to a specific problem. It's to build a mental model so strong that you can solve the next problem, even if it looks a little different.

The Power of a Mistake Journal

One of the most powerful, low-tech tools you have is a simple notebook. It might sound a little backward, but focusing on your mistakes is one of the fastest ways to get better.

Grab a notebook and call it your "mistake journal." For every problem you get wrong on homework or a quiz, log these four things:

1. The Original Problem: Write it down, clean and clear.
2. Your Incorrect Solution: This is crucial. Write out your flawed logic so you can see it.
3. The Correction: Pinpoint exactly where you went wrong. Was it a simple arithmetic error? Did you forget a trig identity? Did you misunderstand the chain rule? Be specific.
4. The Takeaway: In one sentence, write down what you'll do differently next time to avoid making that same mistake.

Before you know it, this journal will reveal your personal patterns. Maybe you always mess up negative exponents, or you consistently forget to add + C to your indefinite integrals. Once you see the pattern, you know exactly what to focus on. To really nail calculus, you have to try different effective study methods, and this is one of the best to have in your toolkit.

A Few Common Questions I Hear About Calculus

Even with a solid game plan, some questions always seem to pop up when students are trying to get the hang of calculus. Let's walk through a few of the most common hurdles I've seen over the years. Getting these things straight can be a real game-changer.

The goal isn't just to get the right answer, but to actually understand how you got there.

What’s the Single Biggest Mistake Students Make in Calculus?

Honestly, the most common mistake has nothing to do with calculus itself. It's a shaky foundation in algebra and trigonometry. The core ideas in calculus can be pretty intuitive, but the actual work—the nitty-gritty steps to solve a problem—is almost always heavy algebraic lifting.

Forgetting your exponent rules, log properties, or trig identities will stop you in your tracks before you even start the calculus. If you're stuck, take a breath and ask yourself: is this a calculus problem, or is it an algebra problem?

The best thing you can do for your calculus grade is to spend time reviewing your algebra. Seriously. It pays off more than anything else.

How Do I Know Which Integration Technique to Use?

Ah, the classic question. The honest answer is experience and pattern recognition. But you can speed that process up by not just guessing randomly. Instead, build a little mental checklist.

When you see an integral, run through this sequence in your head:

• Is it just a basic rule? Always check your formula sheet first. Sometimes a scary-looking integral is just a basic antiderivative you need to recognize.
• Can I use u-substitution? This is your workhorse. Look for a function "nested" inside another, where its derivative is also hanging around.
• Is it a product of two different types of functions? If you see something like x * sin(x) or e^x * cos(x), your mind should immediately jump to integration by parts.
• Is it a big fraction with polynomials? If you have a polynomial divided by another polynomial, partial fraction decomposition is likely the way to go.

Thinking this way turns a shot in the dark into a systematic process. You’ll be surprised how quickly you start seeing the patterns.

Why Can I Follow the Lecture but Can’t Do the Homework?

This is so, so common. It highlights the difference between passively watching and actively doing. Following along as a professor explains a solution is one thing; creating that solution from a blank page is a completely different skill.

The fix is to be more active from the get-go. While your professor works through an example, try to stay one step ahead of them. When you get stuck, that’s your learning moment. That's the exact spot you need to focus on.

Use office hours, your study group, or an AI tool to figure out that specific step. Your goal is to practice the entire thought process on your own, not just memorize the steps someone else took.

---

Stuck on a tricky step or need a concept explained a different way? Feen AI can be like a personal tutor, walking you through the logic of tough calculus problems. Just upload a picture of your homework to get the help you need to move forward. Give it a try for free at https://feen.ai.