How to Find the Derivative of a Function A Practical Guide

When you're asked to find the derivative of a function, what you're really doing is figuring out its instantaneous rate of change at any given point. Think of it as finding the slope of a curve at a single, specific moment. This process reveals precisely how quickly a value is changing. We can do this the long way, using the limit definition from first principles, or much more efficiently by applying a set of standard differentiation rules.

What Finding a Derivative Really Means

Before we get tangled up in formulas, it's essential to have a solid gut feeling for what a derivative is. At its heart, a derivative is a precision tool for measuring change. It answers the question, "How fast is this function changing right now?"

Imagine you’re driving a car. Your average speed for the whole trip is just the total distance divided by the total time. It gives you a decent overview, but it doesn't tell you much about any specific moment. The derivative, on the other hand, is like glancing down at your speedometer—it shows your exact speed at that precise instant.

This concept of instantaneous change is the core idea behind all of differential calculus.

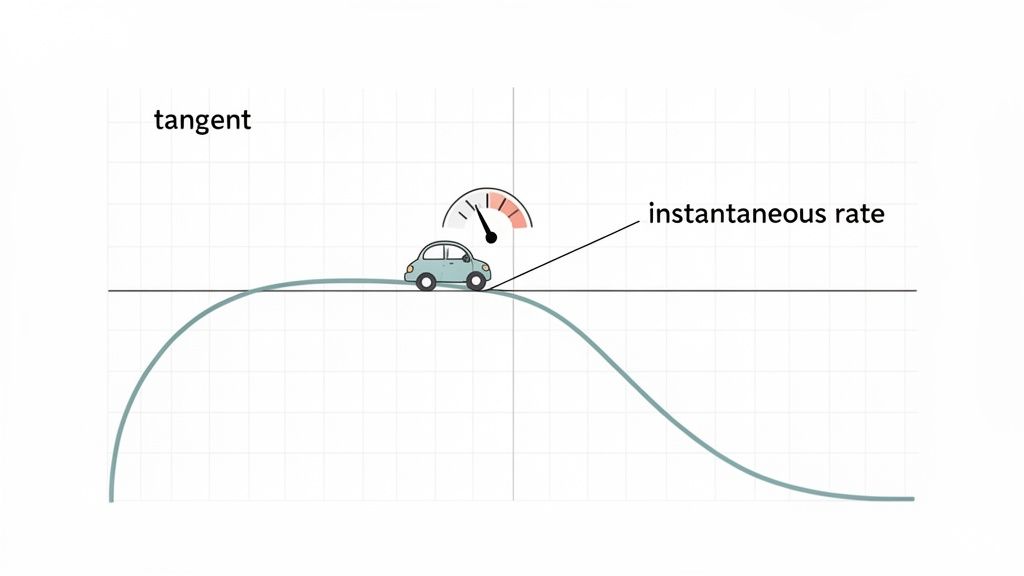
The Visual Interpretation: Slope of the Tangent Line

Graphically, the derivative has a very concrete meaning: it’s the slope of the line that just barely kisses the curve of a function at one specific point. We call this special line the tangent line. If a function's graph is steep, its derivative will be a large number. If the graph is flat, its derivative is zero.

Grasping this visual connection is a game-changer. It turns the abstract task of finding a derivative into something you can actually see and interpret on a graph. Building this foundation makes the rules you'll learn later feel less like random formulas and more like logical tools. For a deeper look at these core ideas, our guide on https://feen.ai/blog/how-to-understand-calculus is a great place to start.

Real-World Applications of Derivatives

This isn't just theory for a math class; derivatives are fundamental to how we describe the world. They show up everywhere:

• Modeling motion: In physics, the derivative of a position function tells you an object's velocity. The derivative of velocity gives you its acceleration.
• Optimizing processes: Businesses use derivatives to pinpoint the exact production levels needed to maximize profit or minimize costs.
• Analyzing trends: Economists apply them to calculate the rate of inflation or economic growth at a specific moment in time.

To really see how practical derivatives are, it's helpful to see them in action. Checking out some real-world physics projects shows how these math tools are used to describe everything from the orbit of planets to the flow of electricity in a circuit.

The concept of a derivative has a surprisingly long history. Its roots go back more than a millennium to 12th-century mathematics. The Indian mathematician Bhaskara II was working with early ideas of infinitesimal change way back in 1150 CE. Not long after, the Persian mathematician Sharaf al-Dīn al-Tūsī became the first person to discover the derivative of cubic polynomials.

Deriving from Scratch with the Limit Definition

Before we get to all the handy shortcut rules, it's worth taking a look at where derivatives actually come from. This is what we call finding a derivative "from first principles," and it all comes down to one core formula: the limit definition of a derivative.

Honestly, once you learn the rules, you won't use this method for day-to-day problems. But understanding it is the key to truly getting what a derivative is. It's the engine under the hood. It forces you to see the derivative for what it is—the slope of a tangent line at a single point, found by taking the slope of a secant line between two points and nudging those points infinitely close together.

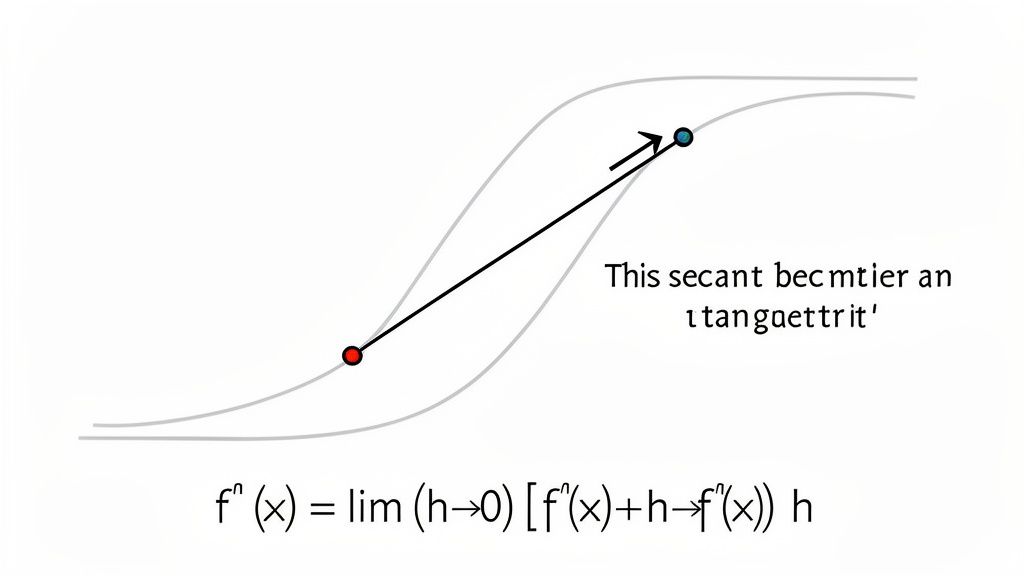
Unpacking the Limit Definition Formula

The formula itself can look a little intense at first, but it’s really just a dressed-up version of the "rise over run" slope formula you learned in algebra. Here it is:

f'(x) = lim(h→0) [f(x+h) - f(x)] / h

Let's break that down. The [f(x+h) - f(x)] / h part is just the slope between two points on our function's graph. We have one point at (x, f(x)) and a second point just a tiny horizontal distance, h, away at (x+h, f(x+h)).

The magic is in the lim(h→0) part. This tells us to see what happens as we make that horizontal distance h shrink all the way to zero. As h gets smaller, our two points get closer and closer, and the slope of the line connecting them morphs into the exact slope at the single point x.

Think of it like this: You're calculating your average speed between two mile markers. As you move those markers closer together—say, a mile apart, then a hundred feet, then just one foot—your average speed becomes a much better estimate of your instantaneous speed right at that spot. The limit is the math that lets us close that gap to zero.

A Worked Example: Finding the Derivative of x²

Let's walk through a classic example to see how the algebra plays out: finding the derivative of f(x) = x² using the limit definition.

Our goal is to plug f(x) = x² into the formula and simplify it until we can safely let h become zero.

• Set up the formula. We need to find f(x+h). To do this, we just replace every x in our function with (x+h). So, f(x+h) = (x+h)². Now we can plug everything into the definition:
  f'(x) = lim(h→0) [ (x+h)² - x² ] / h

• Expand and simplify. The next move is to expand the (x+h)² term. A super common mistake is to forget the middle term! Remember that (x+h)² = x² + 2xh + h².
  f'(x) = lim(h→0) [ (x² + 2xh + h²) - x² ] / h

• Cancel out terms. You'll notice we have an x² and a -x² in the numerator. They cancel each other out, which is exactly what we want to see. This cancellation is a critical milestone in the process.
  f'(x) = lim(h→0) [ 2xh + h² ] / h

• Factor out h. Now, look at what’s left on top—every term has an h in it. Let's factor that out.
  f'(x) = lim(h→0) [ h(2x + h) ] / h

• Cancel h and evaluate. The h we just factored out cancels with the h in the denominator. This is the key step that gets us out of the 0/0 jam and lets us finally evaluate the limit.
  f'(x) = lim(h→0) [ 2x + h ]

Now, we can let h go to zero. What are we left with? Just 2x.

So, we get our final answer: f'(x) = 2x.

This algebraic workout shows precisely why the derivative of x² is 2x. You'll soon use the Power Rule to get this answer in a second, but going through the limit definition builds a solid foundation. It's the "why" behind all the "how-to" rules.

Building Your Derivative Toolkit with Essential Rules

Working through the limit definition is fantastic for understanding why derivatives work, but let's be honest—it's like building furniture with just a handsaw. It gets the job done, but it's slow and painful. It's time to add some power tools to your mathematical workshop.

These essential differentiation rules are the shortcuts that let you find the derivative of a function quickly and efficiently. Think of them less as formulas to memorize and more as fundamental tools. Once you get the hang of them, you can combine them in all sorts of ways to tackle almost any problem that comes your way.

We'll start with the three rules that form the bedrock of differentiation: the Power Rule, the Constant Rule, and the Sum/Difference Rule.

The Power Rule: Your Go-To for Exponents

The Power Rule is, without a doubt, the most frequently used tool in your entire derivative toolkit. It gives you a simple, direct way to find the derivative of any function that looks like f(x) = xⁿ, where 'n' can be any real number.

The rule itself is beautifully straightforward: you bring the exponent down to the front as a multiplier and then just subtract one from the original exponent.

Power Rule Formula: If f(x) = xⁿ, then f'(x) = n * xⁿ⁻¹

Let's see this in action with something like f(x) = x³. Following the rule, we bring the 3 down to the front and subtract 1 from the exponent.

• Original function: f(x) = x³
• Apply the rule: f'(x) = 3 * x³⁻¹
• Resulting derivative: f'(x) = 3x²

And that's it. This one rule lets you find the derivative of x², x¹⁰, or even x⁻² in seconds, saving you from wrestling with the limit definition every single time.

The Constant Rule: The Easiest Rule in Calculus

Next up is the Constant Rule, which is probably the easiest rule you'll learn in all of calculus. It applies to functions that are just a single number, like f(x) = 5 or f(x) = -12.

A constant function is just a perfectly flat, horizontal line on a graph. Since a derivative measures the slope or rate of change, and a horizontal line has zero slope, it makes perfect sense that the derivative of any constant is always zero.

Constant Rule Formula: If f(x) = c (where c is a constant), then f'(x) = 0

So, if you have the function f(x) = 7, its graph is a horizontal line sitting at y=7. There's no change, no steepness, and therefore no slope. Its derivative is simply f'(x) = 0. This might seem obvious, but it’s a crucial piece of the puzzle, especially when constants show up in more complex functions.

Combining Functions with the Sum and Difference Rule

Most functions you'll encounter will have multiple terms added or subtracted, like f(x) = x⁴ + x². The Sum and Difference Rule tells us exactly how to handle these. It says you can find the derivative of the whole function by simply taking the derivative of each piece individually and keeping the original plus or minus signs between them.

This is where your toolkit really starts to come together, because now you can use the Power Rule on each term separately.

Example Problem
Let's find the derivative of g(x) = 4x³ - 5x² + 2x - 9.

We'll just go through it term by term:

1. The derivative of 4x³: The derivative of x³ is 3x². We multiply that by the 4 out front to get 4 * 3x² = 12x².
2. The derivative of -5x²: The derivative of x² is 2x. Multiply by the -5 to get -5 * 2x = -10x.
3. The derivative of 2x: Remember that x is the same as x¹. The derivative is 1 * x⁰ = 1. So, we have 2 * 1 = 2.
4. The derivative of -9: This is just a constant, so its derivative is 0.

Now, we just string those results back together: g'(x) = 12x² - 10x + 2.

This ability to break a bigger problem into smaller, manageable chunks is a core idea in math. These foundational rules were nailed down in the late 17th century, largely thanks to Gottfried Wilhelm Leibniz. In 1677, he figured out the rules for products, quotients, and composite functions—the very same rules we still teach today. You can read more about Leibniz's groundbreaking work in calculus and see how it shaped modern mathematics.

With just these three rules in hand, you're already equipped to find the derivative of any polynomial function out there.

To help you keep these straight, here's a quick cheat sheet for the basic rules we've covered so far. It's a great reference to have handy as you start practicing.

Quick Reference Basic Differentiation Rules

Rule Name	Formula Notation	Example
Constant Rule	If f(x) = c, then f'(x) = 0	If f(x) = 5, then f'(x) = 0
Power Rule	If f(x) = xⁿ, then f'(x) = n * xⁿ⁻¹	If f(x) = x⁴, then f'(x) = 4x³
Constant Multiple	If f(x) = c * g(x), then f'(x) = c * g'(x)	If f(x) = 3x², then f'(x) = 3 * (2x) = 6x
Sum/Difference Rule	If h(x) = f(x) ± g(x), then h'(x) = f'(x) ± g'(x)	If h(x) = x³ + 2x, then h'(x) = 3x² + 2

Mastering these foundational rules is your first major step. Once they feel like second nature, you'll be ready to move on to more advanced techniques for tackling even more complex functions.

Tackling Complex Functions with Advanced Techniques

Once you've got the basic rules down, you're ready to move beyond simple polynomials. Most real-world problems involve functions that are multiplied, divided, or even nested inside one another. This is where you'll need a few more specialized, powerful techniques.

These methods—the Product Rule, the Quotient Rule, and the Chain Rule—are the real workhorses of differential calculus. They give you a systematic way to break down and solve derivatives, no matter how intimidating they look at first glance.

Differentiating Multiplied Functions with the Product Rule

So, what happens when your function is the product of two other functions, like f(x) = x² * sin(x)? A common mistake is to just find the derivative of each part and multiply them together. Unfortunately, calculus isn't quite that simple. This is exactly what the Product Rule is for.

The rule gives you a clear formula for this situation. If you have a function h(x) made by multiplying f(x) and g(x), here’s how you find its derivative:

Product Rule Formula: If h(x) = f(x) * g(x), then h'(x) = f(x)g'(x) + g(x)f'(x)

Put simply, it's the first function times the derivative of the second, plus the second function times the derivative of the first.

Putting the Product Rule to Work

Let's find the derivative of h(x) = x² * sin(x).

• First, identify your two functions: f(x) = x² and g(x) = sin(x).
• Next, find their derivatives: f'(x) = 2x and g'(x) = cos(x).
• Now, plug them into the formula: h'(x) = (x²)(cos(x)) + (sin(x))(2x).
• Finally, simplify the result: h'(x) = x²cos(x) + 2xsin(x).

This methodical process keeps you from making easy mistakes when dealing with multiplied functions.

Handling Fractions with the Quotient Rule

Just as we have a rule for multiplication, we also have one for functions that are fractions, like h(x) = eˣ / x³. This is where the Quotient Rule comes in. It's a bit more complex than the Product Rule, and getting the order right is absolutely critical.

The formula can be tricky to remember, which is why so many students use a little mnemonic: "Low D-High minus High D-Low, all over Low squared." In this phrase, "Low" is the denominator, "High" is the numerator, and "D" means "the derivative of."

Quotient Rule Formula: If h(x) = f(x) / g(x), then h'(x) = [g(x)f'(x) - f(x)g'(x)] / [g(x)]²

That minus sign in the numerator is precisely why the order matters so much.

Putting the Quotient Rule to Work

Let's find the derivative of h(x) = eˣ / x³.

• Identify "High" and "Low": The numerator, f(x) = eˣ, is "High." The denominator, g(x) = x³, is "Low."
• Find their derivatives: f'(x) = eˣ and g'(x) = 3x².
• Apply the formula: h'(x) = [ (x³)(eˣ) - (eˣ)(3x²) ] / (x³)².
• Simplify: h'(x) = [ x³eˣ - 3x²eˣ ] / x⁶. We can factor out x²eˣ from the top, which gives us h'(x) = x²eˣ(x - 3) / x⁶. This simplifies down to h'(x) = eˣ(x - 3) / x⁴.

The Chain Rule for Nested Functions

You could argue that the Chain Rule is the most important and versatile of the advanced rules. You'll use it anytime you have a "function within a function"—what mathematicians call a composite function. Think of expressions like f(x) = (x² + 1)³ or g(x) = cos(5x).

I like to think of these as Russian nesting dolls. There's an "outer" function and an "inner" function. The Chain Rule tells you to take the derivative of the outer function (leaving the inside part alone for a moment) and then multiply that result by the derivative of the inner function.

Chain Rule Formula: If h(x) = f(g(x)), then h'(x) = f'(g(x)) * g'(x)

Putting the Chain Rule to Work

Let's use the Chain Rule on h(x) = (x² + 1)³.

• Outer function: Think of this as f(u) = u³, where u is the inner stuff. Its derivative is f'(u) = 3u².
• Inner function: This is the part inside the parentheses, g(x) = x² + 1. Its derivative is g'(x) = 2x.
• Combine them: Now, put it all together. h'(x) = 3(x² + 1)² * (2x) = 6x(x² + 1)².

This "outside-in" approach makes it possible to differentiate incredibly complex expressions one piece at a time. When you're just starting out, it can be tough to know which rule to grab. This little decision tree can help clear things up.

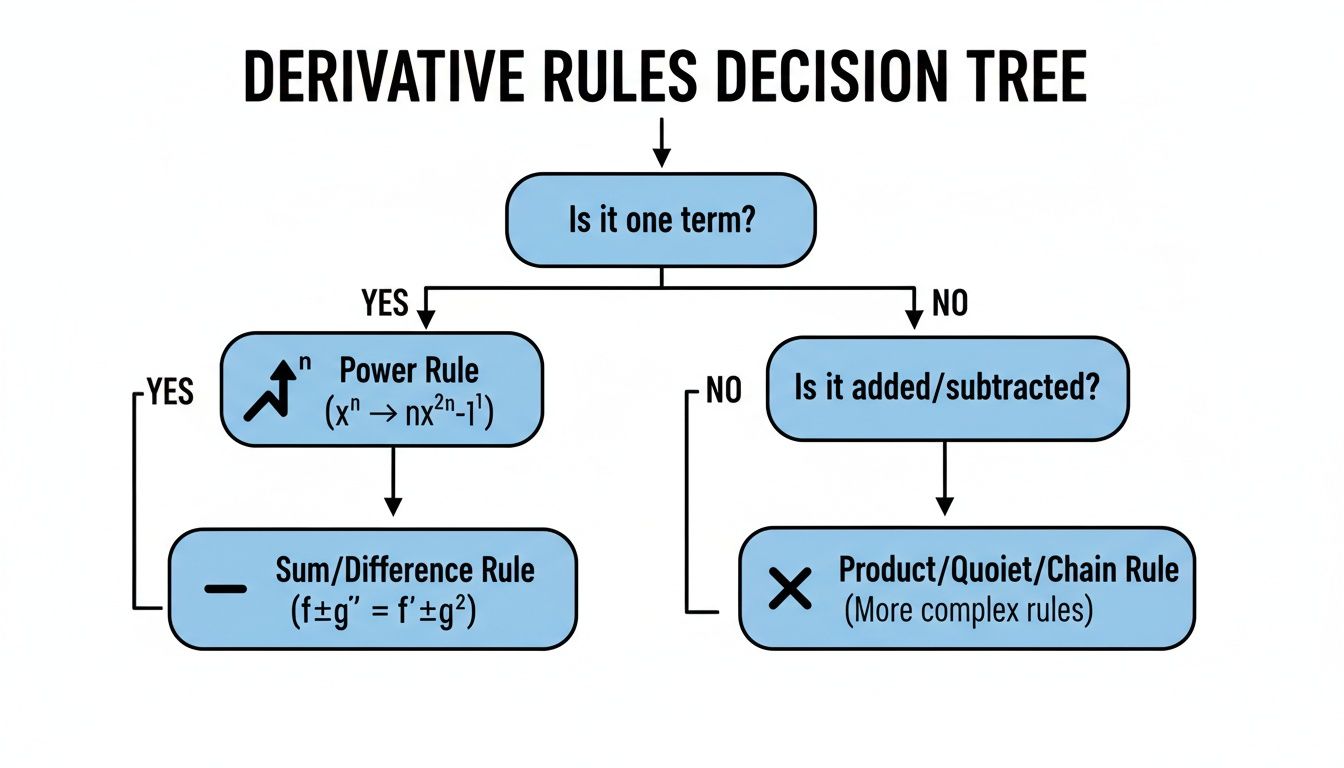
As the chart shows, the structure of the function—whether it's a single term, a sum, a product, a quotient, or nested—is what tells you which rule you need to apply.

Implicit Differentiation for Complex Relations

So what do you do when you have an equation you can't easily solve for y? A perfect example is the equation for a circle, x² + y² = 25. This isn't a simple y = f(x) function. For situations like this, we have a clever technique called Implicit Differentiation.

The main idea is to differentiate both sides of the equation with respect to x, but here's the trick: you have to treat y as a function of x. This means that whenever you differentiate a term with y in it, the Chain Rule kicks in, and you have to multiply by dy/dx.

Putting Implicit Differentiation to Work

Let's find dy/dx for our circle equation, x² + y² = 25.

1. Differentiate both sides with respect to x: This looks like d/dx(x²) + d/dx(y²) = d/dx(25).
2. Apply the rules to each term:
   • The derivative of x² with respect to x is just 2x.
   • The derivative of y² needs the Chain Rule: it becomes 2y * dy/dx.
   • The derivative of the constant 25 is 0.
3. This gives you a new equation: 2x + 2y(dy/dx) = 0.
4. Now, just solve for dy/dx:
   • 2y(dy/dx) = -2x
   • dy/dx = -2x / 2y
   • dy/dx = -x/y

This powerful result gives you the slope of the tangent line at any point (x, y) on the circle, even though we never had to solve for y explicitly.

Avoiding the Most Common Derivative Mistakes

Working with derivatives is a bit like learning a new language—you'll make a few common mistakes before you become fluent. Even students who feel confident can get tripped up by a few classic pitfalls. Knowing what to watch for is half the battle.

Let's break down the errors I see most often so you can steer clear of them.

Forgetting the Chain Rule

This is, without a doubt, the number one mistake. It's so easy to look at a function like f(x) = sin(x²) and just jump to differentiating the sin part. But that's only half the story. The Chain Rule is your tool for any composite function, which is just a fancy way of saying a function tucked inside another one.

Take f(x) = (3x + 1)⁴. This is a textbook "function within a function."

• The Common Mistake: Applying only the Power Rule to the outside gives you 4(3x + 1)³. This feels right, but it's incomplete. You've completely ignored the inner part, 3x + 1.

• The Correct Approach: You have to multiply by the derivative of that inner function. The derivative of 3x + 1 is simply 3. So, the full, correct answer is f'(x) = 4(3x + 1)³ * 3, which simplifies to 12(3x + 1)³.

Here’s my go-to tip: If you see parentheses with something more complicated than just 'x' inside, or if a function is acting on another function, your "Chain Rule alarm" should be ringing.

Mixing Up the Quotient Rule

Another major trouble spot is the Quotient Rule. Its formula is a little clunky compared to the Product Rule, and it’s incredibly common to mix up the order of the terms in the numerator. That minus sign makes the order absolutely critical.

To get it right every single time, just memorize this little rhyme: "Low D-High minus High D-Low, all over Low squared."

Let's try it with g(x) = x² / cos(x).

• The Common Mistake: If you flip the terms in the numerator, you get [ (x²)( -sin(x) ) - (cos(x))(2x) ] / cos²(x). This simple swap inverts the sign of your final answer, making it completely wrong.

• The Correct Approach: Stick to the rhyme. "Low" is cos(x) and "High" is x². "D-High" is 2x, and "D-Low" is -sin(x). Plugging that in gives you [ (cos(x))(2x) - (x²)(-sin(x)) ] / cos²(x). Cleaned up, that's (2x*cos(x) + x²*sin(x)) / cos²(x).

Simple Rule and Algebra Errors

Finally, a lot of points are lost to basic slip-ups that have nothing to do with the complex rules. One I see all the time is trying to use the Power Rule on exponential functions like eˣ. Remember, the Power Rule is for variables raised to a constant (xⁿ), not for constants raised to a variable (aˣ). The derivative of eˣ is its own special case: it’s just eˣ.

It’s also crucial to understand the function before you even start. Identifying valid inputs for your function can prevent you from making mistakes later on. If you need a refresher on that, it’s worth learning more about how to find the domain and range to make sure your foundation is solid.

And don't forget to double-check your algebra after you differentiate. A simple simplification error can derail a perfectly calculated derivative. A quick review is all it takes to catch them.

Time to Sharpen Your Pencils: Practice Problems

You can read about derivatives all day, but the only way to truly get them is to roll up your sleeves and get your hands dirty. This is where the theory hits the road. Working through problems is what builds the instinct and the confidence you need to look at any function and know exactly how to break it down.

I’ve put together a few problems here to test your skills. They start off fairly straightforward and then ramp up, forcing you to combine rules and really think through your approach.

The Problem Set

Give each of these a shot. The goal isn't to be perfect right away; it's to see what clicks and what still feels a little fuzzy.

1. Find the derivative of f(x) = 7x⁴ - 3x² + 8x - 1
2. Find the derivative of g(t) = (t³ + 4) * eᵗ
3. Find the derivative of h(x) = sin(x) / x²
4. Find the derivative of y = (5x² - 2x)⁶
5. Find dy/dx for the equation x³ + y³ = 6xy

These problems are a solid starting point. If you want to dig deeper into building a solid problem-solving routine, our guide on how to solve calculus problems has some great strategies that can make a real difference.

Let's Break Down the Solutions

Okay, let's walk through these together. Compare this with what you came up with—it's the best way to spot any little misunderstandings in the process.

Problem 1 Solution: The Basics
f(x) = 7x⁴ - 3x² + 8x - 1

This one is a great warm-up, testing the Power, Constant Multiple, and Sum/Difference rules. All you have to do is tackle each term on its own.

• The derivative of 7x⁴ becomes 7 * 4x³ = **28x³**.
• The derivative of -3x² becomes -3 * 2x = **-6x**.
• The derivative of 8x is just 8.
• The derivative of the constant -1 is 0.

Putting it all together, you get the final answer.

Final Answer: f'(x) = 28x³ - 6x + 8

Problem 2 Solution: Product Rule in Action
g(t) = (t³ + 4) * eᵗ

Here we have two functions multiplied together, which is a dead giveaway for the Product Rule. Remember the formula: (first * d(second)) + (second * d(first)).

• First function: (t³ + 4)
• Second function: eᵗ
• Derivative of the first: 3t²
• Derivative of the second: eᵗ (this one's easy!)

Now, we just plug these pieces into the formula: g'(t) = (t³ + 4)(eᵗ) + (eᵗ)(3t²). A little cleanup by factoring out the eᵗ gives us a much neater answer.

Final Answer: g'(t) = eᵗ(t³ + 3t² + 4)

Problem 3 Solution: Taming the Quotient Rule
h(x) = sin(x) / x²

A function divided by another function? Time for the Quotient Rule.

• High (numerator): sin(x)
• Low (denominator): x²
• D-High (derivative of numerator): cos(x)
• D-Low (derivative of denominator): 2x

Now, apply the formula: h'(x) = [ (x²)(cos(x)) - (sin(x))(2x) ] / (x²)². Don't forget to simplify!

Final Answer: h'(x) = (x*cos(x) - 2*sin(x)) / x³

A quick tip from my own student days: "Low D-High minus High D-Low, all over Low squared." Saying that little rhyme to myself saved me from mixing up the numerator order more times than I can count.

Problem 4 Solution: Unraveling the Chain Rule
y = (5x² - 2x)⁶

This is a textbook "function inside of a function," which is the classic signal for the Chain Rule.

• The "outer" function: Think of it as u⁶. Its derivative is 6u⁵.
• The "inner" function: u = 5x² - 2x. Its derivative is 10x - 2.

The Chain Rule tells us to multiply the derivative of the outside by the derivative of the inside.

dy/dx = 6(5x² - 2x)⁵ * (10x - 2)

Final Answer: dy/dx = (60x - 12)(5x² - 2x)⁵

Problem 5 Solution: Implicit Differentiation
x³ + y³ = 6xy

This one looks tricky because you can't easily solve for y. That's where implicit differentiation comes in. We just differentiate both sides with respect to x, treating y as a function of x.

• x³ becomes 3x².
• y³ becomes 3y² * dy/dx (that's the Chain Rule!).
• 6xy needs the Product Rule: (6x)(dy/dx) + (y)(6).

So our equation becomes: 3x² + 3y²(dy/dx) = 6x(dy/dx) + 6y. The rest is just algebra—get all the dy/dx terms on one side and solve.

3y²(dy/dx) - 6x(dy/dx) = 6y - 3x²
dy/dx * (3y² - 6x) = 6y - 3x²

Final Answer: dy/dx = (6y - 3x²) / (3y² - 6x)

---

Feeling stuck on a specific calculus concept or need a step-by-step walkthrough for a tough problem? With Feen AI, you can upload a picture of your homework and get clear, detailed explanations instantly. It's like having a personal tutor available 24/7 to help you understand the concepts and master the material. Try it now and see how much faster you can learn at https://feen.ai.