How to solve logarithmic equations - A Step-by-Step Guide

Staring down an equation with "log" peppered all over it can be intimidating. It looks like a completely different kind of math, but it's not. Really, it's just a new way of asking a familiar question.

At its heart, a logarithm is just looking for a missing exponent. When you see log₂(8), the equation is asking, "What power do I need to raise 2 to in order to get 8?" The answer is 3, since 2³ = 8. That's it.

This back-and-forth relationship between logarithms and exponents is the key to everything. They're two sides of the same coin. Being able to flip between logarithmic form (logₐ(x) = y) and exponential form (aʸ = x) is the number one trick you'll use to solve these problems.

Before you can start solving, though, you need the right tools. For logs, that means mastering three core properties. These aren't just random rules to memorize; they are the specific techniques you'll use to simplify messy equations and get them into a solvable form. Think of them as the grammar rules for the language of logarithms.

Your Toolkit: The Three Core Properties of Logarithms

These properties are your best friends when it comes to combining or breaking apart logarithms, and they mirror the exponent rules you already know.

• The Product Rule: This rule lets you combine two logs that are being added together. The log of a product is just the sum of the individual logs. In math terms: logₐ(MN) = logₐ(M) + logₐ(N).
• The Quotient Rule: Just like addition and multiplication go together, subtraction and division are a pair. The log of a fraction (a quotient) is the log of the top minus the log of the bottom: logₐ(M/N) = logₐ(M) - logₐ(N).
• The Power Rule: This one is a game-changer. It lets you take an exponent from inside a log and move it out front as a multiplier. The formula is logₐ(Mᵖ) = p * logₐ(M). This is your go-to move for getting a variable out from an exponent.

These ideas might feel modern, but they've been around for a while. Logarithms were actually invented back in the 17th century by a Scottish mathematician named John Napier who was looking for a way to make grueling multiplication and division problems simpler for astronomers. He figured out he could turn multiplication into addition and division into subtraction—exactly what these rules do!

Key Takeaway: You absolutely must know the product, quotient, and power rules inside and out. Almost every logarithmic equation you'll face will require you to use one or more of them to simplify the problem first.

For students who want a helping hand, AI tools can offer instant, step-by-step guidance on applying these concepts. You can see how platforms like Feen AI can help you work through tricky homework problems.

To make these rules stick, here’s a handy reference table.

Essential Logarithm Properties at a Glance

This table is a great cheat sheet to keep nearby while you're working. It summarizes the three fundamental rules you'll be using constantly.

Property Name	Rule Formula	Example
Product Rule	log_b(MN) = log_b(M) + log_b(N)	log₂(3) + log₂(x) = log₂(3x)
Quotient Rule	log_b(M/N) = log_b(M) - log_b(N)	log(10) - log(2) = log(10/2) = log(5)
Power Rule	log_b(M^p) = p * log_b(M)	ln(x⁴) = 4 * ln(x)

Once you're comfortable with these properties, you'll be ready to condense, expand, and manipulate any logarithmic equation that comes your way.

Core Strategies for Common Log Equations

Alright, now that you've got the essential log properties under your belt, it's time to actually use them. When you're staring down a logarithmic equation, it will almost always fall into one of two main categories. The first, and luckily the simplest, is an equation with just a single logarithm.

Your game plan here is pretty direct: get the log term by itself on one side of the equation. Once you’ve isolated it, you can just rewrite the whole thing in its exponential form. This move completely gets rid of the logarithm and leaves you with a standard algebra problem you already know how to solve.

Let's walk through a quick one.

The Single-Log Scenario

Consider an equation like this: 2 * log₃(x + 1) = 4

First things first, you need to isolate that log term. Just divide both sides by 2.

log₃(x + 1) = 2

Now, you simply convert it to its exponential form. Remember, the base is 3, the exponent is 2, and the argument is (x + 1).

3² = x + 1

From here, it's just basic algebra.

9 = x + 1
x = 8

Don't forget the final, crucial step: check your answer. Plug it back into the original equation to make sure you aren't taking the log of a negative number or zero. In this case, log₃(8 + 1) is log₃(9), which is perfectly fine.

Tackling Equations with Multiple Logarithms

The other common situation is finding multiple log terms in one equation, sometimes on both sides of the equals sign. Your strategy has to change a bit here. Instead of trying to isolate a log, your main goal is to condense.

This is where you'll lean on the product and quotient rules to combine all the logarithms on each side into a single log. Once you get the equation into the form logₐ(M) = logₐ(N), you can use what’s called the one-to-one property of logarithms. It basically says that if two logs with the same base are equal, then their arguments have to be equal too. So, you can just drop the logs and solve M = N.

This infographic gives a great visual for deciding which path to take.

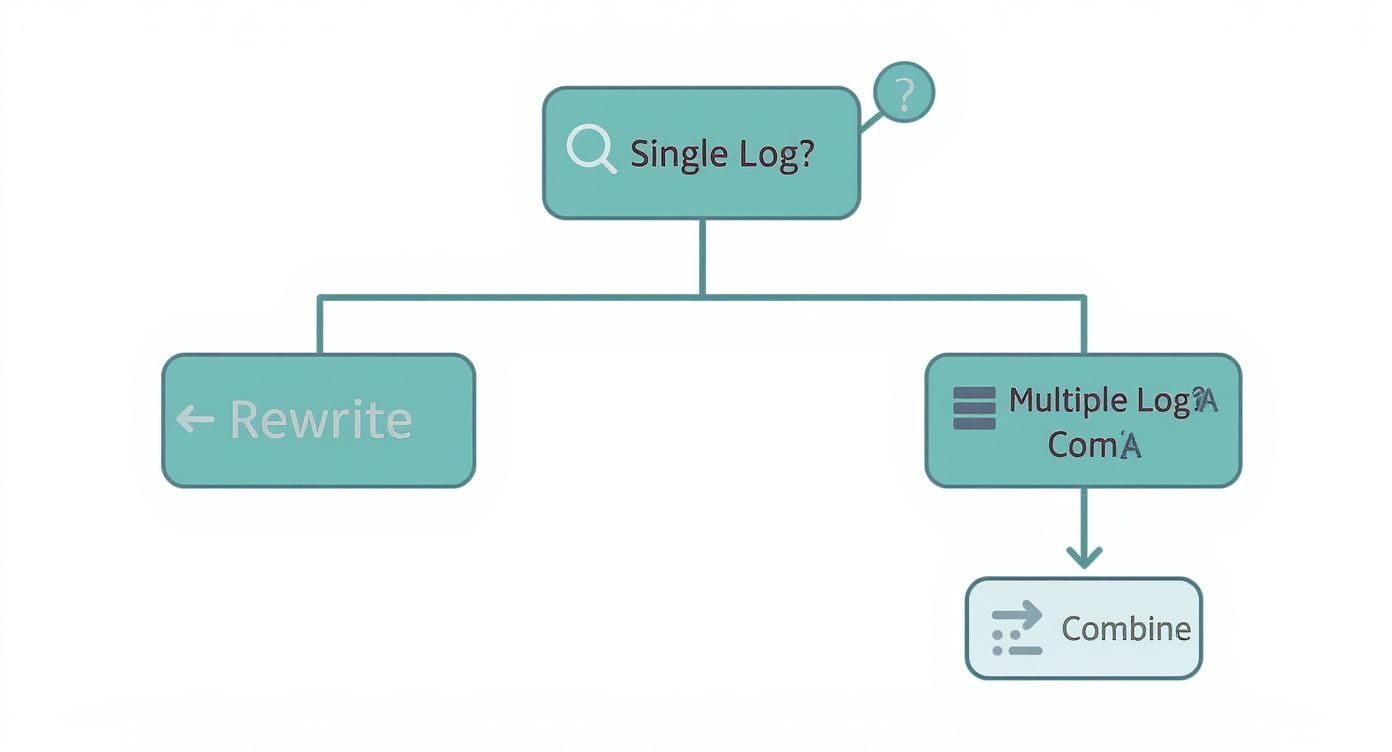
Think of it as a quick decision tree: see one log, rewrite it. See multiple logs, combine them first.

Condensing and Solving in Action

Let's put this condensing strategy to work with a tougher example.

Imagine you're given: log₂(x) + log₂(x - 2) = 3

• Condense the logs first. The logs are being added, so we can use the product rule to merge them into one.
  log₂(x * (x - 2)) = 3
log₂(x² - 2x) = 3

• Rewrite in exponential form. Now that it's a single log, we can convert it.
  2³ = x² - 2x
8 = x² - 2x

• Solve the new equation. This time, we've ended up with a quadratic. To solve it, get everything on one side and set the equation to zero.
  x² - 2x - 8 = 0
(x - 4)(x + 2) = 0

This gives us two potential solutions: x = 4 and x = -2.

Critical Check: You absolutely have to verify both answers in the original equation. Plugging in x = 4 gives log₂(4) + log₂(2), which works. But if you plug in x = -2, you get log₂(-2) + log₂(-4). Since you can't take the logarithm of a negative number, x = -2 is an extraneous solution. You have to throw it out. The only real answer is x = 4.

This whole process relies on some pretty old mathematical ideas. A logarithm is just asking, 'What power do I need to raise the base to, to get this other number?' By applying rules that have been around since the 17th century, we can turn tricky multiplication problems into simple addition. If you're interested, you can explore more about the history and rules of logarithms to get a deeper appreciation for how it all fits together.

Solving Advanced and Tricky Log Equations

So, you've gotten the hang of the standard log equations. That's great! But let's be honest, exams love to throw a few curveballs. This is where we shift gears and tackle the trickier problems—the ones that need a bit more finesse and a couple of extra tools in your math toolkit. Mastering these strategies is what separates a good student from a great one.

Sometimes, a problem will try to throw you off by mixing different log bases in the same equation. When you see that, your first thought should be, "How can I make these bases match?" This is where a super handy tool called the change of base formula saves the day.

Handling Logs with Different Bases

The change of base formula is your secret weapon for rewriting any logarithm in terms of a more useful base. The formula itself is logₐ(b) = logₓ(b) / logₓ(a). You can pick any new base 'x' you want, but the most practical choices are almost always base 10 (the common log, log) or base e (the natural log, ln). Why? Because your calculator has dedicated buttons for them.

Let's put it into practice with an equation like log₂(x) + log₄(x) = 6.

You can't just combine these logs because the bases (2 and 4) are different. The trick is to use the change of base formula to turn log₄(x) into a base-2 logarithm.

• Apply the formula: log₄(x) = log₂(x) / log₂(4)
• Simplify the bottom part: We know log₂(4) is simply 2, because 2² = 4.
• Substitute it back in: This means log₄(x) is the same as (1/2) * log₂(x).

Now, our original equation becomes something much more manageable: log₂(x) + (1/2) * log₂(x) = 6.

From here, it's smooth sailing. Combine the like terms to get (3/2) * log₂(x) = 6. Solving for the log term gives us log₂(x) = 4. And finally, converting to exponential form gives us 2⁴ = x, so x = 16.

Pro Tip: When you spot different bases in a problem, look for a relationship between them. In our example, 4 is a power of 2. That’s a massive clue that converting everything to the smaller base (base 2) is your most efficient path to the answer.

When Log Equations Disguise Themselves as Quadratics

Some of the most intimidating log equations are actually just familiar algebra problems wearing a clever disguise. A classic trick is hiding a quadratic equation inside the logarithmic structure. The key to spotting these is to look for a pattern: a squared log term, a regular log term, and a plain old number.

Check out this equation: (ln(x))² + ln(x) - 2 = 0.

Doesn't that structure look a lot like ax² + bx + c = 0? It absolutely is. To make it obvious, we can use a technique called u-substitution. Let's just temporarily set u = ln(x).

Substituting u into our equation makes it instantly recognizable: u² + u - 2 = 0.

This is a simple quadratic we can factor in our sleep: (u + 2)(u - 1) = 0. That gives us two potential solutions for u: u = -2 and u = 1.

But hold on, we're solving for x, not u. We have to substitute ln(x) back in.

• For u = -2: ln(x) = -2. Rewriting this in exponential form gives e⁻² = x.
• For u = 1: ln(x) = 1. Rewriting gives e¹ = x.

So, our two solutions are x = e⁻² (which is just 1/e²) and x = e. Since both values are positive, they are both valid. This is a fantastic trick for turning a scary-looking problem into something you’ve already solved a hundred times.

Using Logs to Solve for Variables in Exponents

What do you do when the variable you need is stuck up in an exponent and you can't make the bases match? This is the exact scenario where logarithms become your best friend.

Imagine you're faced with 5ˣ = 14.

There's no easy way to write 14 as a power of 5. The only way to get that x down from the exponent is to take the logarithm of both sides. You can use either the common log (log) or the natural log (ln). Both work perfectly, but you'll find that ln is more common in higher-level math.

1. Take the natural log of both sides:
   ln(5ˣ) = ln(14)

2. Use the power rule: This is the magic step. The power rule of logs lets you bring that exponent x down to the front as a multiplier.
   x * ln(5) = ln(14)

3. Isolate x: At this point, ln(5) and ln(14) are just numbers you can get from your calculator. To solve for x, just divide.
   x = ln(14) / ln(5)

Punching that into a calculator, you'll see ln(14) ≈ 2.639 and ln(5) ≈ 1.609. This gives us our final answer: x ≈ 1.64.

The ideas behind logarithms didn't just appear out of nowhere. They're deeply connected to the natural logarithm and exponential functions, which are the bedrock of calculus. The natural log, ln, is based on Euler's number e (~2.71828), a constant that Jacob Bernoulli first stumbled upon around 1683 while studying compound interest. Later, the great Leonhard Euler formalized its relationship to logs in the 18th century. If you're curious, you can read about the history of these mathematical tools to see how these powerful concepts came to be.

How to Spot and Handle Extraneous Solutions

So, you've crunched the numbers. You used the log properties, isolated the variable, and found a value for x. You're ready to circle that answer and move on, right? Not so fast.

With logarithmic equations, there's a crucial final step that trips up even the sharpest students: checking your work for extraneous solutions. These are sneaky answers that look perfectly fine on paper but are actually invalid when you plug them back into the original equation.

This whole issue boils down to one fundamental rule: you can't take the logarithm of a negative number or zero. The algebraic steps we use to solve these problems don't always account for this domain restriction, which is why a final check isn't just a good idea—it's absolutely mandatory.

Why Do These Fake Solutions Even Show Up?

Let's break down where they come from. Say you're using the Product Rule to combine log(x) + log(x - 3) into log(x(x - 3)). When you do this, you subtly change the rules of the game.

The original problem demands that both x and x - 3 are positive. The combined version only needs their product to be positive. Think about it: two negative numbers multiplied together also result in a positive, a scenario the original equation would never allow. This tiny shift is how an invalid answer can slip through your algebra. It's not that you did the math wrong; it's that the process itself can introduce solutions that don't fit the original puzzle.

The Golden Rule of Log Equations: Always, always plug your final answers back into the very first equation you started with. It's the only guaranteed way to catch an extraneous solution before it costs you points.

A Practical Walkthrough

Let’s watch an extraneous solution appear in the wild. We'll solve this equation:

log₆(x + 5) + log₆(x) = 2

First, we'll use the Product Rule to condense the two logs on the left.

• log₆(x * (x + 5)) = 2
• log₆(x² + 5x) = 2

Next, we switch to exponential form to get rid of the logarithm.

• 6² = x² + 5x
• 36 = x² + 5x

Now it’s a standard quadratic equation. Let's move everything to one side and solve.

• x² + 5x - 36 = 0
• (x + 9)(x - 4) = 0

This gives us two potential solutions: x = -9 and x = 4. If you stopped here, you'd be in trouble. It’s time to check them.

The All-Important Final Check

Let's plug each answer back into our original equation: log₆(x + 5) + log₆(x) = 2.

• Checking x = 4:
  log₆(4 + 5) + log₆(4) = 2
log₆(9) + log₆(4) = 2
  A quick calculator check shows 1.226 + 0.774 is indeed 2. This solution works. It’s valid.

• Checking x = -9:
  log₆(-9 + 5) + log₆(-9) = 2
log₆(-4) + log₆(-9) = 2
  And we can stop right there. You can't take the log of -4 or -9. The moment you see a negative number inside a logarithm's argument, you've found an imposter.

So, x = -9 is an extraneous solution. We have to throw it out. The only real answer to this problem is x = 4. Forgetting to check is hands-down the most common pitfall with these equations, so burn this step into your problem-solving routine.

Time to Sharpen Your Pencils: Practice Problems

Knowing the rules is one thing, but actually using them is where the magic happens. Real confidence comes from getting your hands dirty, working through problems, and seeing the patterns for yourself. This is your chance to build that muscle memory and make solving log equations feel like second nature.

I've put together a few problems that slowly ramp up in difficulty, touching on all the strategies we've covered. Don't just rush to an answer. The goal is to pause, identify what kind of problem you're looking at, and then consciously choose the right tool for the job.

Laying the Foundation

Let's start with the basics. These first two problems are all about the core mechanics—condensing logs and swapping between log and exponential forms. Get these down, and you'll be set for the tougher stuff.

• Problem 1: Solve log₅(2x - 3) = 2
• Problem 2: Solve ln(x) + ln(x - 2) = ln(3)

Walkthrough 1: log₅(2x - 3) = 2

This is a classic single-log equation. The move here is to rewrite it in its exponential form to free the variable.

5² = 2x - 3
25 = 2x - 3
28 = 2x
x = 14

Just to be safe, let's plug it back in: log₅(2(14) - 3) = log₅(28 - 3) = log₅(25). Since 5² = 25, our answer is solid.

Walkthrough 2: ln(x) + ln(x - 2) = ln(3)

This time, we have logs on both sides. The first step is to clean up the left side by condensing it with the Product Rule.

ln(x * (x - 2)) = ln(3)
ln(x² - 2x) = ln(3)

Thanks to the one-to-one property, if the natural logs are equal, their insides must be equal too.

x² - 2x = 3
x² - 2x - 3 = 0
(x - 3)(x + 1) = 0

This gives us two potential answers: x = 3 and x = -1. But remember, we have to check! Plugging x = 3 into the original equation works perfectly. Plugging in x = -1 gives us ln(-1), which is a big no-no. So, x = -1 is an extraneous solution, and our only real answer is x = 3.

Upping the Ante: Intermediate Challenges

Okay, time to add a few more layers. These problems will bring in some more complex algebra and really test your ability to spot those sneaky extraneous solutions.

• Problem 3: Solve log(x) + log(x + 21) = 2
• Problem 4: Solve 2 * log₃(x) = log₃(2x + 8)

Walkthrough 3: log(x) + log(x + 21) = 2

First, condense the left side with the Product Rule.

log(x(x + 21)) = 2
log(x² + 21x) = 2

Don't forget that a plain log has an invisible base of 10. Now, let's switch to exponential form.

10² = x² + 21x
100 = x² + 21x
x² + 21x - 100 = 0
(x + 25)(x - 4) = 0

We get x = -25 and x = 4. A quick check shows that x = -25 would force us to take the log of a negative number in the original equation, so it's out. The only valid answer is x = 4.

Walkthrough 4: 2 * log₃(x) = log₃(2x + 8)

See that coefficient out front? That's our cue to use the Power Rule. Let's move that 2 up into the log as an exponent.

log₃(x²) = log₃(2x + 8)

Now we have a single log on each side with the same base, so we can set their arguments equal.

x² = 2x + 8
x² - 2x - 8 = 0
(x - 4)(x + 2) = 0

Our potential solutions are x = 4 and x = -2. As before, plugging x = -2 into the original equation doesn't work. That leaves x = 4 as our final answer.

Getting into the habit of neatly documenting your steps is crucial, not just for getting the right answer but for understanding your own thought process. It's a lot like learning how to write an essay fast; outlining your ideas first makes the final product so much stronger.

Key Takeaway: There's no substitute for practice when it comes to mastering logarithmic equations. The more problems you solve, the more you'll develop an instinct for which rule to use and a healthy habit of always checking your work for those tricky extraneous solutions.

Answering Your Top Questions About Logs

Even after you've got the main strategies down, a few questions always seem to pop up. Think of this as a quick FAQ session to iron out any last-minute wrinkles in your understanding. We'll clear up the real difference between the log and ln buttons on your calculator, explain why you can't plug negative numbers into a log, and pinpoint the best times to use the change of base formula.

Getting these details straight is often the final step toward walking into a test with total confidence. Let's make sure nothing catches you by surprise.

What’s the Real Difference Between Log and Ln?

You've definitely seen both the LOG and LN buttons on your calculator. While they aren't the same, the only thing that separates them is the base they're built on.

• LOG is the common log. Whenever you see log(x) without a tiny number tucked beside it, it automatically means base 10. It's basically asking, "10 raised to what power gives me x?" You'll see this pop up a lot in science, like with the pH scale for acidity or the Richter scale for earthquakes.

• LN is the natural log. This one always uses a special number called Euler’s number (e ≈ 2.718) for its base. So, ln(x) is just a shorter way to write logₑ(x). It's asking, "e raised to what power gives me x?" The natural log is a huge deal in calculus and shows up everywhere in models for continuous growth, like compound interest and population change.

Here's the most important thing to remember: even though their bases are different, both log and ln follow the exact same product, quotient, and power rules. You solve an ln equation using the same moves you'd use for a log equation.

So, Why Can’t You Take the Log of a Negative Number?

This is one of the most important rules in the world of logarithms, and it's the whole reason we have to check for those pesky extraneous solutions. The answer goes right back to what a logarithm actually is.

Remember, an equation like log_b(x) = y is just a different way of writing the exponential equation b^y = x. For logs to work with real numbers, the base b has to be a positive number other than 1.

Now, think about what happens when you raise a positive number to any power you can think of.

• 2³ = 8 (Positive)
• 2⁻³ = 1/8 (Still positive!)
• 2⁰ = 1 (Also positive)

It doesn't matter what real exponent y you pick; a positive base b raised to that power can never spit out a negative number or zero. Since b^y is always positive, the x it equals must also be positive. That’s why the "argument"—the stuff inside the parentheses of a log—must always be greater than zero.

When Do I Actually Need the Change of Base Formula?

The change of base formula is a fantastic tool, but you definitely don't need to use it for every problem. It's really the hero in two specific situations.

1. Solving Equations with Mismatched Bases: This is its star role. If you run into something like log₂(x) + log₄(x) = 6, you can't just combine the logs because their bases (2 and 4) are different. The change of base formula is how you convert them into a common base (like base 2, log, or ln) so you can actually solve the equation.

2. Using Your Calculator: Most calculators only have buttons for base 10 (log) and base e (ln). If you're asked to find the value of log₇(50), you're stuck, right? Not with this formula. It lets you turn that problem into something your calculator can handle, like log(50) / log(7) or ln(50) / ln(7).

Nailing down these finer points will get you ready for whatever your teacher throws at you. For more study guides and deep dives into other topics, feel free to check out other resources on the Feen AI blog.

---

Stuck on a tricky problem or need someone to walk you through a tough concept? Feen AI is like having an expert tutor on demand. Just snap a picture of your homework, and our AI will guide you through the solution, making sure you understand the "why" behind the steps so you're prepped for your next exam. Give it a try at https://feen.ai.