How to Solve Trigonometric Identities (how to solve trigonometric identities)

Solving a trigonometric identity is a bit like a puzzle. The trick is to start with the more complicated side of the equation and, step-by-step, transform it until it looks exactly like the simpler side. You do this by strategically swapping in fundamental identities, recognizing patterns, and simplifying as you go.

Your success hinges on knowing a core set of formulas—the Reciprocal, Quotient, and Pythagorean identities. Getting these down cold is the absolute first step.

Building Your Foundational Trig Identity Toolkit

Before you even think about tackling a proof, you need to get your tools in order. Think of these foundational identities as the essential instruments you'll use to take equations apart and put them back together in a new way.

Each identity has a specific job. Some let you swap out terms, others help you rewrite expressions, and a few are perfect for breaking down complexity. Just like a mechanic needs more than a single wrench, you need a variety of identities in your back pocket. Success really starts with mastering the three core families of identities. They are the bedrock of trigonometry and pop up in almost every problem.

Let's break down the essential formulas you'll need. Think of this table as your go-to reference when you're just starting out.

The Core Trigonometric Identities Toolkit

Identity Type	Formula	Key Relationship
Reciprocal	sin(θ) = 1/csc(θ)	Defines the inverse relationship between sine and cosecant.
	cos(θ) = 1/sec(θ)	Defines the inverse relationship between cosine and secant.
	tan(θ) = 1/cot(θ)	Defines the inverse relationship between tangent and cotangent.
Quotient	tan(θ) = sin(θ)/cos(θ)	Expresses tangent as a ratio of sine and cosine.
	cot(θ) = cos(θ)/sin(θ)	Expresses cotangent as a ratio of cosine and sine.
Pythagorean	sin²(θ) + cos²(θ) = 1	The cornerstone identity, directly from the unit circle.
	1 + tan²(θ) = sec²(θ)	Derived from the main Pythagorean identity by dividing by cos²(θ).
	1 + cot²(θ) = csc²(θ)	Derived from the main Pythagorean identity by dividing by sin²(θ).

These identities aren't just formulas to memorize; they are the fundamental rules that govern how trigonometric functions relate to one another.

The Reciprocal and Quotient Identities

The most direct tools you have are the Reciprocal and Quotient identities. They spell out the basic relationships between the six trig functions. Reciprocal identities are all about inversion—how one function is simply the multiplicative inverse of another.

• Reciprocal Identities: These let you flip functions. For instance, csc(θ) is just another way of writing 1/sin(θ), and cot(θ) is the same as 1/tan(θ).
• Quotient Identities: These show how one function can be written as a ratio of two others. The big ones are tan(θ) = sin(θ)/cos(θ) and cot(θ) = cos(θ)/sin(θ).

These are your best friends when you want to convert an entire messy equation into just sines and cosines, which is a fantastic simplifying strategy we'll cover soon.

Key Takeaway: The goal is to see identities as interchangeable parts. When you see tan(x), your brain should immediately think, "I can swap that for sin(x)/cos(x) if it helps me simplify."

The Pythagorean Identities

Next up are the Pythagorean identities, which come straight from the Pythagorean theorem (a² + b² = c²) applied to the unit circle. These are incredibly useful for getting rid of squared terms or, sometimes, for creating them when you need them.

The main one you absolutely must know is sin²(θ) + cos²(θ) = 1. From this single formula, we can easily derive the other two:

• 1 + tan²(θ) = sec²(θ)
• 1 + cot²(θ) = csc²(θ)

These three are crucial for simplifying expressions that have a "1" in them or for converting between squared sine and cosine terms. It's fascinating to think that the groundwork for these relationships was laid around 140 BCE by Hellenistic astronomers like Hipparchus of Nicaea, whose work on chord tables essentially kicked off the whole field of trigonometry.

This isn't about rote learning; it's about building fluency. For some great tips on committing these to memory, check out our guide on how to study math effectively.

Expanding Your Arsenal with Advanced Identities

Once you get comfortable with the foundational identities, you’ll inevitably run into problems that just don't cooperate. Those basic tools won't cut it. This is where the more advanced identities come into play, helping you break down complex angles and tackle those really stubborn expressions.

Think of these not as longer formulas to memorize, but as strategic tools for specific situations. Mastering these is a huge step in learning how to solve trigonometric identities, especially the more sophisticated ones. It’s a shift from simple substitutions to actively expanding, contracting, and transforming the angles themselves. This takes a sharp eye for patterns and knowing exactly when to deploy each formula.

Sum and Difference Formulas

Ever been stumped by something like cos(x + y) or asked to find the exact value of sin(75°) without a calculator? The Sum and Difference formulas are built for this. They let you break apart or combine angles inside a trig function.

These are especially handy when you’re dealing with angles that aren't the usual 30°, 45°, or 60°, but can be made from them. For example, you can rewrite sin(15°) as sin(45° - 30°) and solve it from there. It's a neat trick.

Here are the formulas you'll need:

• Sine of a Sum/Difference: sin(A ± B) = sin(A)cos(B) ± cos(A)sin(B)
• Cosine of a Sum/Difference: cos(A ± B) = cos(A)cos(B) ∓ sin(A)sin(B)
• Tangent of a Sum/Difference: tan(A ± B) = (tan(A) ± tan(B)) / (1 ∓ tan(A)tan(B))

Pay close attention to the sign changes in the cosine and tangent formulas—it's a classic spot for a small mistake. A good mental shortcut is that cosine's formula "flips" the operational sign, while sine's keeps it the same.

Double-Angle and Half-Angle Identities

So, what do you do when you see a sin(2x) or cos(x/2)? This is a clear signal to use the Double-Angle and Half-Angle identities. They are perfectly designed for simplifying expressions where an angle is being multiplied or divided by two.

These identities actually come directly from the Sum formulas. If you take sin(A + B) and just set A = B, you get the double-angle formula: sin(2A) = 2sin(A)cos(A). The journey to this simple notation was a long one; the systematic use of sin and cos was refined over centuries, with major leaps in the 17th and 18th centuries by mathematicians like Leonhard Euler. You can explore more on the origins of trigonometric functions to see how these ideas grew.

Spotting when to use these is a skill. If one side of an identity has an angle of 2θ and the other side just has θ, that's your cue to use a double-angle formula to get the angles on both sides to match.

Pro Tip: The double-angle identity for cosine is a real workhorse and comes in three forms. Choosing the right one can save you a ton of work.

• cos(2A) = cos²(A) - sin²(A)
• cos(2A) = 2cos²(A) - 1 (Use this when you want to get rid of sines)
• cos(2A) = 1 - 2sin²(A) (Use this when you want to get rid of cosines)

Recognizing When to Use Advanced Identities

Knowing the formulas is one thing, but knowing when to pull them out is the real art. The structure of the problem itself usually drops some big hints about which tool to grab.

Deciding which advanced identity to apply often comes down to recognizing specific patterns in the problem. The table below outlines common scenarios and which identity is your best bet.

Strategic Use of Advanced Identities

Identity Type	Common Problem Structure	Example Application
Sum/Difference	An angle is shown as a sum or difference, like cos(π/2 - x).	Use the difference formula to expand it into cos(π/2)cos(x) + sin(π/2)sin(x), which quickly simplifies to sin(x).
Double-Angle	One side of the equation has an angle of 2x while the other side only has x.	To prove (sin(2x))/(1+cos(2x)) = tan(x), you'd substitute 2sin(x)cos(x) for sin(2x) and 2cos²(x)-1 for cos(2x).
Half-Angle	You need an exact value for an unconventional angle like 15° or 22.5°.	Use the half-angle formula for cos(x/2) to find the precise value of cos(22.5°) by setting x = 45°.

Developing this kind of pattern recognition just takes practice. The more identities you solve, the more these choices will feel intuitive, turning your approach from guesswork into a confident, strategic process.

Proven Strategies for Navigating Any Proof

Knowing the identities is one thing, but actually using them to solve a proof is a whole different ballgame. It's less about rote memorization and more about developing a strategic intuition. You have to look at a jumbled equation and see the path forward—knowing which tool to pull from your toolbox and when.

Think of it less like following a strict recipe and more like solving a puzzle. Each proof is unique and demands a bit of creative thinking. This is where you move from just knowing the formulas to becoming a genuine problem-solver. Let's break down a reliable game plan that works for almost any identity you'll encounter.

Start with the More Complicated Side

This is the number one rule, the one I tell every student to live by. Always begin on the side of the equation that looks messier, longer, or more complex. Why? Because it’s so much easier to simplify something than it is to build it up from scratch.

It’s like tidying a messy room. You have plenty of things (terms and functions) to move around, combine, and condense. Trying to work from the simple side is like starting with an empty room and trying to create a specific, chaotic scene—it's way harder and far less intuitive.

For example, if you're asked to prove (sin²(x) + cos²(x)) / cos²(x) = sec²(x), you’d be making your life difficult by starting with sec²(x). The left side is practically begging you to simplify it.

Convert Everything to Sines and Cosines

When you hit a wall and no obvious substitutions are jumping out at you, fall back on this tried-and-true strategy. Take every function in the expression and rewrite it purely in terms of sine and cosine.

• tan(x) becomes sin(x)/cos(x)
• cot(x) becomes cos(x)/sin(x)
• sec(x) becomes 1/cos(x)
• csc(x) becomes 1/sin(x)

This move effectively levels the playing field. What was once a chaotic mix of six different trig functions now becomes a more manageable algebraic expression with just two variables. More often than not, this simple conversion reveals opportunities to cancel terms, find a common denominator, or spot a Pythagorean identity you didn't see before.

Look for Algebraic Moves

Don't get so caught up in the trigonometry that you forget your algebra fundamentals! Sometimes, the key to unlocking a proof isn't a fancy identity but a basic algebraic maneuver. Be on the lookout for these classic moves:

• Factoring: Can you pull out a greatest common factor? An expression like sin(x) - sin(x)cos²(x) is a perfect candidate. Factor out sin(x) to get sin(x)(1 - cos²(x)), and you're already halfway there.
• Combining Fractions: If you see two or more fractions, find a common denominator and merge them into a single term. This almost always cleans up the expression.
• Multiplying by a Conjugate: This is a fantastic trick. If you spot a binomial like 1 - sin(x) in the denominator, try multiplying both the numerator and denominator by its conjugate, 1 + sin(x). This creates a difference of squares (1 - sin²(x)), which beautifully simplifies to cos²(x).

This flowchart offers a visual guide for choosing the right path when dealing with more advanced identities.

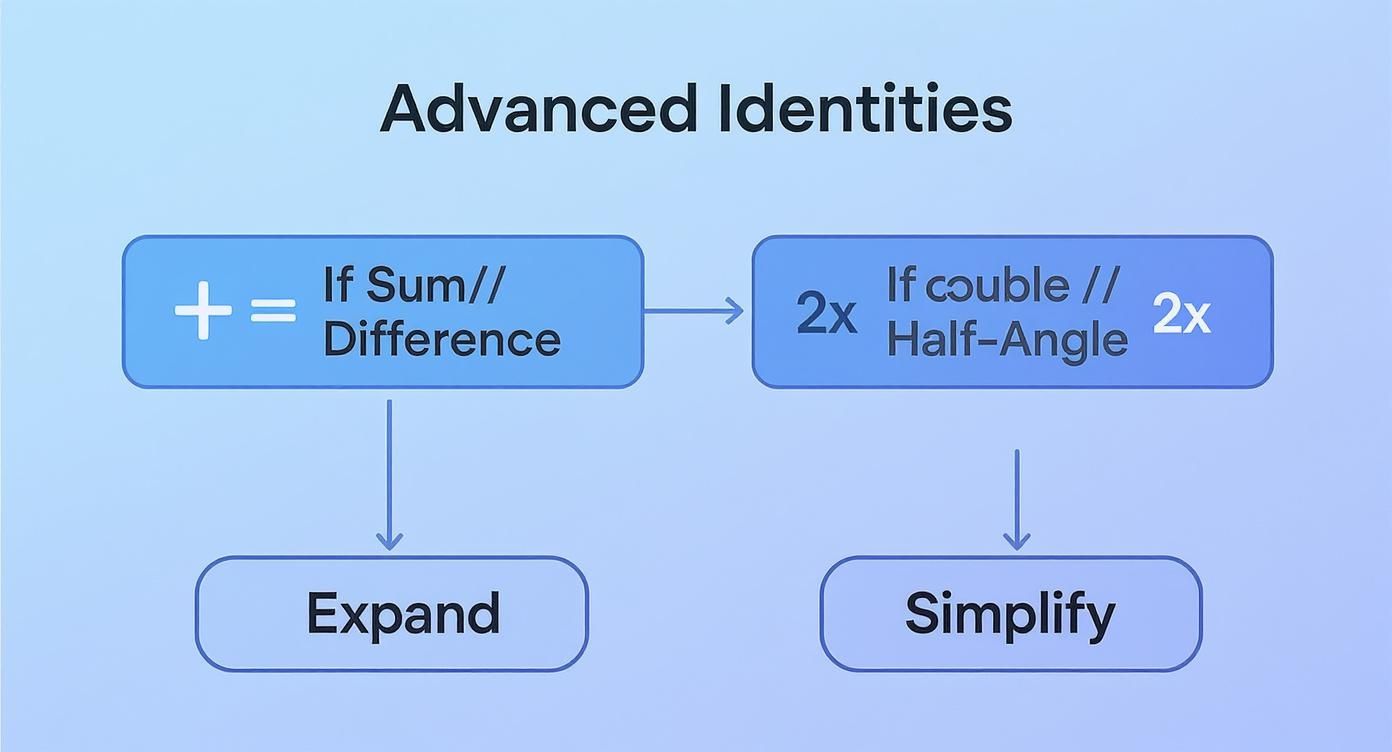
As the chart shows, your first move is to identify the angle's structure—is it a sum, difference, double, or half-angle? That will tell you whether you need to expand or simplify.

Key Insight: Proving an identity isn't about finding one magical step. It's a process of taking small, logical bites out of the problem. Each substitution should make the expression a little bit simpler. If your move makes it more complicated, you’ve probably taken a wrong turn.

Mastering these strategies just takes practice. With time, you'll start to recognize the patterns instinctively. To keep your skills sharp, it helps to incorporate engaging learning strategies into your study routine.

Ultimately, solving these proofs builds confidence and sharpens your problem-solving mind. If you ever feel stuck on the process itself, it can be helpful to review how to solve math problems step-by-step to reinforce a structured approach. Every identity you solve makes the next one that much easier.

Walkthroughs from Simple to Complex Problems

Knowing the rules is one thing, but seeing them in action is where it all clicks. This is where we get our hands dirty and apply those identities and strategies to prove trig identities, moving from the straightforward to the more challenging.

I'm not just going to show you the answers. I want to pull back the curtain on the thought process. What makes you decide to convert everything to sines and cosines? What's the visual cue that screams "use a Pythagorean identity!"?

By breaking down these examples, you'll start to recognize the patterns yourself. That's how you build real confidence and stop staring at a problem, wondering where to even begin.

Example 1: A Straightforward Proof

Let's start with a classic. This one is all about applying the fundamental identities and a little bit of algebra.

Prove: (tan(x) + cot(x)) / sec(x) = csc(x)

Right off the bat, the left side is a jumble of different trig functions, while the right side is a clean, single function. That’s a dead giveaway: start with the more complicated side.

When you're faced with a mix of tan, cot, and sec, the most reliable first move is often to convert everything into its sine and cosine components.

So, let's make those substitutions:

• tan(x) becomes sin(x)/cos(x)
• cot(x) becomes cos(x)/sin(x)
• sec(x) becomes 1/cos(x)

Plugging these in, our expression now looks like this: ((sin(x)/cos(x)) + (cos(x)/sin(x))) / (1/cos(x)). It might look messier for a second, but don't worry. We've just turned a trig problem into an algebra problem.

Cleaning Up the Expression

Now, it's just a matter of simplifying that complex fraction. The first thing to do is handle the numerator by finding a common denominator, which is sin(x)cos(x).

This gives us (sin²(x) + cos²(x)) / (sin(x)cos(x)) in the numerator. The moment you see sin²(x) + cos²(x), a bell should go off in your head. That’s our superstar Pythagorean identity, which equals 1.

The expression simplifies beautifully to (1 / (sin(x)cos(x))) / (1/cos(x)). To divide by a fraction, we just multiply by its reciprocal: (1 / (sin(x)cos(x))) * (cos(x)/1).

The cos(x) terms cancel out, leaving us with 1/sin(x). One last step: the reciprocal identity for 1/sin(x) is csc(x). And just like that, we've transformed the left side into the right side. Proof complete.

Example 2: Using Factoring and Pythagorean Identities

This next one is a great example of how your algebra skills are just as important as your trig knowledge. Here, we need to spot an algebraic opportunity first.

Prove: cos(x) - cos(x)sin²(x) = cos³(x)

Again, we'll attack the more complex left side. There isn't an obvious identity to substitute at first glance. But look closer. Both terms have a common factor: cos(x).

Let's factor it out. This gives us cos(x)(1 - sin²(x)). Now we're getting somewhere. That expression in the parentheses, 1 - sin²(x), should be a huge trigger. Remember sin²(x) + cos²(x) = 1? If you rearrange it, you get cos²(x) = 1 - sin²(x).

Key Takeaway: Always be on the lookout for algebraic moves like factoring or finding a common denominator. Sometimes the biggest breakthrough in a trig proof comes from simple algebra, not a fancy identity.

Now we can substitute cos²(x) back into our expression: cos(x) * cos²(x). This simplifies to cos³(x), which is exactly what we needed to prove.

Example 3: A Complex Proof with Multiple Steps

Alright, let's tackle a more advanced problem. This one introduces a powerful technique called "multiplying by the conjugate," which is a lifesaver when you see a binomial like (1 - sin(x)) in the denominator.

Prove: cos(x) / (1 - sin(x)) = (1 + sin(x)) / cos(x)

Here, both sides look about equally complex, so picking a side is less obvious. Let's just start with the left. That 1 - sin(x) in the denominator is our cue. We're going to multiply the entire fraction by its conjugate, 1 + sin(x), on both the top and bottom.

This move gives us: (cos(x) * (1 + sin(x))) / ((1 - sin(x)) * (1 + sin(x))).

Look at the denominator. We've created a difference of squares, which simplifies to 1 - sin²(x). Sound familiar? As we saw before, that’s just cos²(x).

Our expression is now (cos(x)(1 + sin(x))) / cos²(x). We can cancel out a cos(x) from the numerator and the denominator, leaving us with our final answer: (1 + sin(x)) / cos(x). It's a perfect match for the right side.

Mastering these techniques is crucial, especially for the over 85% of U.S. high school students in advanced math who encounter them. With practice, these steps will become second nature. And if you get stuck on a tricky proof and need a nudge in the right direction, you can always use an AI math solver to check your reasoning without just giving you the final answer.

Common Pitfalls and How to Avoid Them

As you get the hang of how to solve trigonometric identities, you'll quickly realize there are a few common traps that trip up even experienced students. Knowing what these are ahead of time is half the battle. Think of it less as a mistake and more as a wrong turn in a maze—it just means you need to back up and find the right path.

Let's walk through the most common slip-ups I see and, more importantly, how to sidestep them. Catching these early will save you a ton of frustration and help you build smarter problem-solving habits.

Working on Both Sides at Once

This is, without a doubt, the most frequent mistake. Proving an identity is not the same as solving an equation. You can't just add something to both sides or multiply both sides by the same term.

Why not? The whole point is to prove that the two sides are equal. If you start manipulating both sides at the same time, you're assuming they're already equal—which is exactly what you’re trying to demonstrate. It's a classic case of circular reasoning that makes your entire proof invalid.

The Fix: Pick one side and stick with it. I almost always suggest starting with the more complicated-looking side, as it usually gives you more to work with. Your mission is to use valid algebraic steps and identity substitutions to transform that one side until it perfectly matches the other. Never cross the equals sign.

Making Illegal Algebraic Moves

It's surprisingly easy to get so wrapped up in the trigonometry that you forget the fundamental rules of algebra. These little blunders are often the real reason a proof gets stuck, and they can be infuriatingly simple.

Here are a couple of the biggest offenders to watch out for:

• Badly Splitting Fractions: This is a big one. You can’t split a denominator. For example, (1 + cos(x)) / sin(x) correctly becomes 1/sin(x) + cos(x)/sin(x). However, sin(x) / (1 + cos(x)) is not the same as sin(x)/1 + sin(x)/cos(x). It’s a crucial difference.
• Forgetting to Distribute Properly: When you're multiplying, make sure every single term gets included. It seems obvious, but in the heat of the moment, it’s easy to write sin(x) * (1 + tan(x)) as sin(x) + tan(x) instead of the correct sin(x) + sin(x)tan(x).

A quick mental review of your algebra after each step is the best way to catch these little errors before they derail your work.

Forgetting or Misusing Identities

With so many identities to juggle, it’s completely normal to mix them up. A forgotten squared term or a misplaced minus sign can send your entire proof spiraling in the wrong direction.

A prime example is the double-angle formula for cosine, which has three different versions. Using the wrong one can turn a straightforward problem into a messy one. For instance, if the rest of your expression is full of sines, you'll want to use cos(2x) = 1 - 2sin²(x). Choosing cos(2x) = 2cos²(x) - 1 would just introduce cosines you'd have to deal with later.

Here's how to keep them straight:

• Keep a Formula Sheet: Have a neat, organized list of your core identities in front of you while you practice. It’s not cheating; it’s a smart study tool.
• Focus on Pattern Recognition: Don't just memorize the formulas. Learn to recognize the patterns in problems that signal which identity to use.
• Do a Quick Double-Check: After you substitute an identity, just glance back at your sheet to make sure you wrote it down perfectly.

The more you practice, the more these identities become second nature. Soon enough, you'll be spotting these common pitfalls from a mile away and navigating your proofs with confidence.

Clearing Up the Confusion: Your Trig Identity Questions Answered

Even after you've memorized the formulas and reviewed the strategies, it's totally normal to hit a wall when you're wrestling with trig identities. We all get stuck. Sometimes, you just need a nudge in the right direction or a clearer idea of what to focus on.

Let's tackle some of the most common questions that pop up during those late-night study sessions. Think of this as a quick chat with a tutor to help you sharpen your skills and study smarter.

What Do I Do When I'm Completely Stuck?

First off, don't panic. Getting stuck is part of the learning process, not a sign you can't do it. My first piece of advice? Resist the urge to frantically erase everything. Your work so far probably has some good ideas in it.

Take a second to just review what you've already done. Is there a tiny algebraic mistake somewhere? It's amazing how often a dropped negative sign or a simple distribution error is the real culprit. Double-check that you used the right version of an identity.

If your algebra is solid, maybe you just started down the wrong path. That's fine! Go back to the original equation. Perhaps converting everything to sines and cosines wasn't the best first move this time. See if there’s a chance to factor something or if a sneaky Pythagorean identity is hiding in there.

My Go-To Trick: If I'm stuck on a problem for more than 10 minutes, I walk away. Seriously. Go work on something else for a bit. Your brain keeps chewing on the problem in the background, and when you come back, you'll often see the solution immediately.

Which Identities Are the Most Important to Memorize?

Okay, let's be practical. While every identity has its use, some are the absolute superstars you'll use constantly. If your brainpower is limited (and whose isn't?), focus on locking these down first.

You have to know these inside and out:

• The Main Pythagorean Identity: sin²(x) + cos²(x) = 1. This is your desert-island identity. It's the MVP. From this single formula, you can derive the other two Pythagorean identities and solve a huge percentage of problems you'll encounter.
• The Quotient Identities: tan(x) = sin(x)/cos(x) and cot(x) = cos(x)/sin(x). These are the foundation of the "convert everything to sine and cosine" strategy, which is often a lifesaver.
• The Reciprocal Identities: Things like csc(x) = 1/sin(x) might seem basic, but you need them to be second nature.

Once those are burned into your memory, your next priority should be the double-angle formulas. Pay special attention to the three different versions for cos(2x), as they pop up all the time in more complex problems.

How Should I Actually Practice for an Exam?

Watching someone else solve problems or re-reading your notes is passive. To really get good at this, you need active practice. It's the only way to build the intuition and pattern-recognition skills that make solving identities feel less like guesswork and more like a strategy.

I always suggest starting with problems where you have the solutions handy. But don't just glance at the final answer. Go through the proof line by line and ask yourself, "Why did they choose that step right there?" This is how you start thinking like a problem-solver.

Then, it's time to put yourself under a little pressure. Find a set of practice problems and do them in a timed session, with no notes or solutions to guide you. This simulates the real exam environment and helps build your speed and confidence. When you're done, carefully review any mistakes to see where you went off track. Finally, try explaining how to solve a tough problem to a friend. If you can teach it, you know it for real.

---

When you're grinding through practice problems and need a way to check your reasoning, Feen AI can be a huge help. Just snap a photo of the problem, and our AI homework helper will walk you through the logic, step by step. It's perfect for figuring out why a certain step was taken, so you can solve the next one on your own. Get instant, clear explanations for even the trickiest trig identities at https://feen.ai.