8 Types of Math Problems for 1st Graders (2025 Guide)

First grade is a pivotal year where children transition from counting to calculating, building the essential foundation for all future math learning. Understanding the key types of problems they'll encounter is crucial for parents and educators. This guide breaks down core categories of math problems for 1st graders, moving beyond simple worksheets to explore the "why" behind each skill.

We will provide clear examples, strategic teaching tips, and actionable insights to help you support your young learner's journey. Before diving into complex calculations, it's beneficial to ensure a child's foundational readiness is strong. This includes engaging in various fun fine motor skills development activities for kids to improve hand-eye coordination for writing numbers and drawing shapes. This holistic approach prepares them for the specific challenges ahead.

From mastering addition and subtraction to grasping the fundamentals of place value and geometry, this listicle offers the tools to make math engaging and understandable. You will find a curated collection of problems organized by skill, complete with answers and practical tips. This resource is designed to empower you to turn everyday moments into effective learning opportunities, strengthening your first grader’s confidence and competence in mathematics.

1. Simple Addition Problems (Within 10)

Simple addition problems are the cornerstone of first-grade math, focusing on combining two small groups to find a total. These foundational math problems for 1st graders involve sums up to 10, helping children build essential number sense and grasp the core concept of addition: "putting together." This skill transitions them from rote counting to purposeful calculation.

Students first encounter this concept through tangible stories and objects. For instance, "Maria has 3 apples. Her friend gives her 2 more. How many apples does Maria have now?" This concrete approach allows them to physically group items before moving to symbolic representations like "3 + 2 = 5."

Strategic Breakdown

• Concrete to Abstract: The progression is critical. Start with physical items like blocks or toys, then move to drawings, and finally introduce the abstract number sentence (e.g., 4 + 3 = ?). This mirrors cognitive development and solidifies understanding.
• Language Variation: Use diverse language to describe addition. Phrasing like "how many in all," "altogether," and "what is the total" helps students recognize the operation in different contexts.
• Number Bonds: Introduce the concept of number bonds (part-part-whole). Showing that 4 and 3 are "parts" that make the "whole" of 7 builds a mental framework for both addition and subtraction.

Actionable Tips for Practice

To make these problems effective, focus on hands-on engagement and varied practice.

• Manipulative Play: Always have counters, blocks, or even snacks available. Ask the child to build the problem, such as creating a stack of 4 red blocks and 3 blue blocks to find the total.
• Storytelling: Create simple, relatable word problems using the child's name, favorite toys, or daily activities. This makes the math meaningful and engaging.
• Visual Aids: Use a number line for students to practice "counting on." To solve 5 + 3, they start at 5 and "hop" forward three spaces to land on 8.

These foundational skills are crucial, and as students master them, they build the confidence needed for more complex operations. For a look at how these concepts evolve, you can explore the types of math problems for 2nd graders which build directly upon this base.

2. Subtraction Through Removal and Comparison

Subtraction is the natural next step after addition, teaching first graders how to find what remains or determine a difference. These foundational math problems for 1st graders introduce two key scenarios: "taking away" items from a set and "comparing" two different sets. This dual approach helps children understand that subtraction isn't just one action but a concept with multiple real-world applications.

The initial focus is on "take away" problems, which are more intuitive. For example, "There were 7 cookies on a plate. You ate 2. How many are left?" This tangible scenario allows students to physically model the action of removal. Once comfortable, they can tackle comparison problems like, "Sam has 5 toy cars, and Alex has 3. How many more cars does Sam have?"

Strategic Breakdown

• Removal First, Comparison Second: Start with "take away" stories. The physical act of removing objects (e.g., taking two cookies off the plate) makes the abstract concept of subtraction concrete and easy to grasp. Comparison problems, which require a more abstract mental model, should be introduced later.
• Emphasize Key Language: Explicitly teach the language associated with each type of subtraction. Use phrases like "how many are left" for removal problems and "how many more" or "what is the difference" for comparison problems. This helps students identify the correct operation from a word problem.
• Connect to Addition: Frame subtraction as the inverse of addition. For the problem 8 - 3 = 5, show students that this is part of a "fact family" that also includes 3 + 5 = 8 and 5 + 3 = 8. This connection strengthens their number sense and prepares them for more complex algebra later on.

Actionable Tips for Practice

To build a strong subtraction foundation, focus on physical interaction and storytelling.

• Use Manipulatives: Provide counters or small toys. For 8 - 3, have the child count out 8 items and then physically move 3 away. The remaining items are the answer. This visual and tactile process is critical.
• Draw it Out: Encourage students to represent problems visually. They can draw 7 circles, then cross out 2 to find how many are left. This serves as a bridge between concrete objects and abstract number sentences.
• Tell Relatable Stories: Create word problems that involve everyday situations like sharing snacks, losing toys, or comparing collections. Personalizing the problems makes the math more engaging and less intimidating.

3. Number Sense and Counting Activities

Number sense is a student's intuitive understanding of numbers, their magnitude, relationships, and how they are affected by operations. These foundational math problems for 1st graders move beyond rote counting to build a deeper cognitive framework for all future arithmetic. Activities like skip counting, recognizing quantities without counting (subitizing), and understanding number sequences are crucial for developing this flexible thinking.

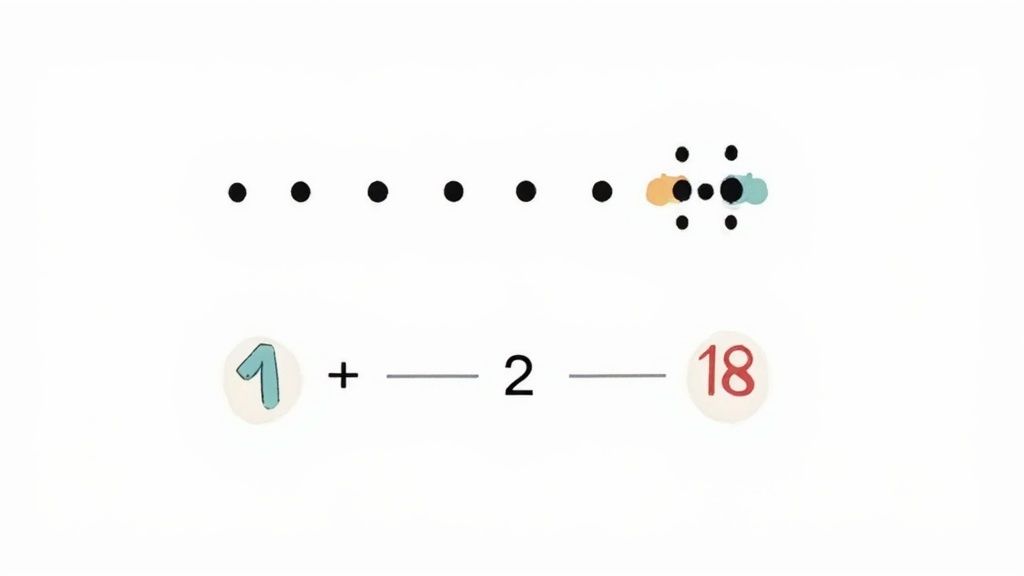
Students engage with number sense when they can quickly identify that a group of 5 dots is larger than a group of 3 without counting each one. They also use it when arranging number cards from 1 to 10 in the correct order or when counting by 10s: 10, 20, 30. This skill is less about finding a single answer and more about internalizing the logic of our number system.

Strategic Breakdown

• From Correspondence to Subitizing: Start with one-to-one correspondence (touching each object as it is counted). Gradually build toward subitizing by flashing dot cards or dice and asking "How many do you see?" This trains the brain to recognize small quantities instantly.
• Sequential Understanding: Focus on number order and what comes "before" and "after." Use a number line or hundreds chart to visually represent sequences, helping students see patterns like how every number in a column ends with the same digit.
• Grouping and Skip Counting: Introduce the concept that numbers can be grouped for faster counting. Clapping or stomping while counting by 2s, 5s, or 10s connects rhythm and movement to numerical patterns, making them more memorable.

Actionable Tips for Practice

To foster a deep understanding of numbers and quantities, hands-on manipulatives and consistent routines are key. For fostering a deep understanding of numbers and quantities, hands-on manipulatives like the Numberblocks Mathlink® Cubes 1-10 Activity Set are excellent.

• Daily Routines: Incorporate counting into daily activities. Count the number of steps to the door, snacks on a plate, or days on a calendar. Ask questions like, "What number comes after today's date?"
• Multisensory Practice: Use songs, chants, and movements to practice skip counting. Playing with dice, dominoes, and finger patterns reinforces subitizing skills in a playful, tactile way.
• Visual Tools: Keep number lines and hundreds charts visible and accessible. These tools serve as constant references, allowing children to independently explore number relationships and patterns.

Developing strong number sense is essential as it provides the foundation for more complex topics, which you can see in our guide to math problems for 3rd graders where these concepts are applied to multiplication and division.

4. Comparison Word Problems

Comparison word problems challenge students to analyze the relationship between two quantities, determining which is greater, which is less, or the exact difference between them. These crucial math problems for 1st graders build relational thinking and go beyond simple computation. They require students to understand and use comparative language like "more," "less," and "fewer," which is a key step toward more complex problem-solving.

These problems are often introduced through relatable scenarios. For example, "Lucy has 6 stickers. Tom has 4 stickers. How many more stickers does Lucy have?" This prompts students not just to count, but to directly compare two sets and find the difference, laying the groundwork for understanding subtraction as a form of comparison.

Strategic Breakdown

• Vocabulary First: Before solving, students must understand the language. Explicitly teach "more," "fewer," "greater than," and "less than." An anchor chart with these terms and visual examples is highly effective.
• Visual Alignment: The key to comparison is one-to-one correspondence. Lining up two sets of objects (e.g., a row of 6 blocks next to a row of 4 blocks) makes it easy for students to see the "extra" ones. This concrete step is essential before moving to abstract drawings or bar models.
• Phased Questioning: Start with simple yes/no or choice questions like, "Who has more?" or "Are there fewer blue buttons?" Once that is mastered, progress to "How many more?" or "How many fewer?" which requires a calculation.

Actionable Tips for Practice

To build confidence with comparison, focus on hands-on activities and consistent language.

• Use Comparison Mats: Create a simple mat with two sections labeled. Have students place groups of objects in each section and physically line them up to compare.
• Story-Based Scenarios: Frame problems around everyday situations. "Our team scored 5 goals and the other team scored 3. How many more goals did we score?" This makes the abstract concept of "difference" tangible.
• Introduce Bar Models: Once comfortable with physical objects, introduce simple bar models (as popularized by Singapore Math). Drawing two bars of different lengths to represent the numbers provides a powerful visual tool for seeing the difference.

5. Place Value with Tens and Ones

Understanding place value is a monumental leap in a first grader's mathematical journey, moving them from counting by ones to grasping the structure of our base-ten number system. These foundational math problems for 1st graders teach that the position of a digit determines its value, decomposing numbers into groups of tens and ones. This concept is the bedrock for comprehending numbers beyond 10 and is critical for future success with multi-digit operations.

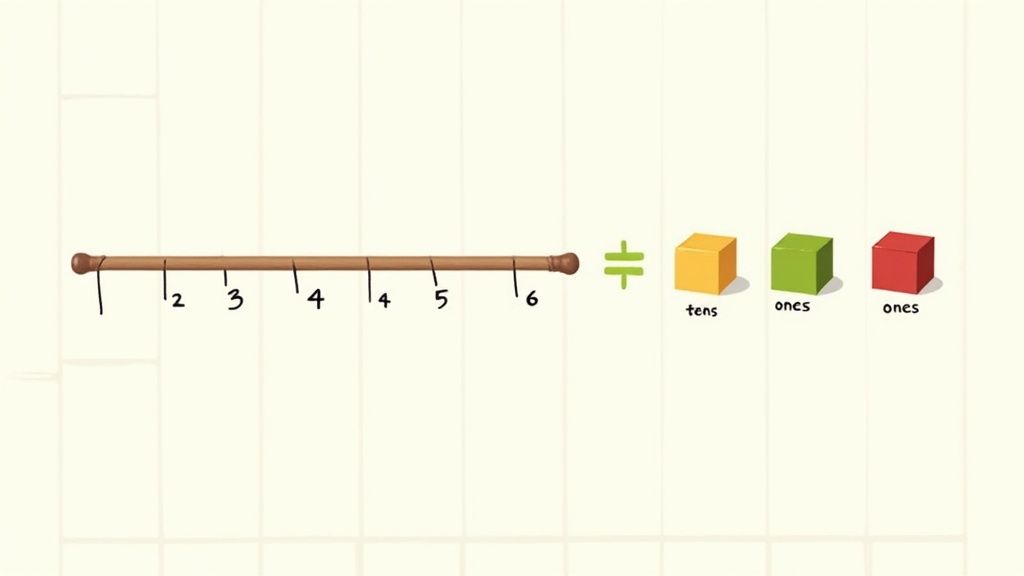
Students are introduced to this by seeing that the number 24 isn't just a collection of 24 individual items, but is more efficiently organized as 2 groups of ten and 4 leftover ones. Problems might ask, "How many tens and ones are in the number 37?" or instruct students to represent 18 using ten frames. This skill bridges counting with true number composition.

Strategic Breakdown

• Concrete Representation: Begin with tangible objects that can be physically grouped. Bundling 10 straws or popsicle sticks with a rubber band creates a concrete "ten" that students can hold and compare to individual "ones."
• Visual Models: Transition from physical items to visual models like base-ten blocks, ten frames, and drawings. These semi-concrete tools help students visualize the "ten-ness" of a number without needing to count every single unit.
• Symbolic Connection: Explicitly connect the physical and visual models to the written number. Laying out 2 ten-rods and 3 unit cubes next to the numeral "23" reinforces that the '2' represents the rods and the '3' represents the cubes.

Actionable Tips for Practice

To build a deep and lasting understanding of place value, use a multi-sensory and consistent approach.

• Build Numbers: Give a child a two-digit number and have them build it using base-ten blocks or by drawing sticks (for tens) and circles (for ones). Ask them to explain their model: "I have 4 tens and 6 ones, so I have 46."
• Use Anchor Charts: Create a large, visible chart in the learning area that clearly shows a number broken into its tens and ones columns with corresponding pictures. This serves as a constant reference point.
• Count and Bundle: Practice counting a collection of more than 10 small items (like beans or pennies). Have the child make groups of ten as they count, bundling them together to see the final composition of tens and ones.

6. Basic Geometry and Shape Identification

Introducing basic geometry provides some of the most hands-on math problems for 1st graders, moving beyond numbers to explore the world of shapes. This area focuses on identifying, describing, and comparing two-dimensional shapes like circles, squares, and triangles. Students learn to recognize these shapes in their environment, laying the groundwork for more complex spatial reasoning.

This skill connects abstract concepts to tangible, everyday objects. For example, a problem might ask, "Find all the rectangles in this picture of a room." Students learn to look for attributes like straight sides and corners, applying their knowledge to real-world contexts and seeing that math is all around them, from a circular clock to a rectangular door.

Strategic Breakdown

• Attributes First: Focus on the language of geometry. Introduce and consistently use terms like sides, corners (or vertices), straight, and curved. This vocabulary is essential for describing and comparing shapes accurately.
• Sorting and Categorizing: Move beyond simple identification to sorting activities. Ask students to group shapes by a specific attribute, such as "shapes with four sides" or "shapes with no corners." This encourages analytical thinking and pattern recognition.
• Compose and Decompose: A key first-grade skill is understanding that shapes can be combined to form larger shapes. For instance, two triangles can be put together to make a square or a larger triangle. This builds a foundational understanding of part-whole relationships in geometry.

Actionable Tips for Practice

To build a strong geometric foundation, make learning interactive and connected to the student's surroundings.

• Shape Hunts: Turn learning into a game. Go on a "shape hunt" in the classroom, at home, or on the playground, having the child identify and name all the circles, squares, and triangles they can find.
• Use Manipulatives: Provide physical shape blocks (pattern blocks) or cutouts. Ask the child to build pictures or patterns with them, encouraging them to name the shapes as they use them.
• Draw and Label: Encourage students to draw shapes and label their parts. For a triangle, they can draw lines pointing to each of the three sides and three corners, reinforcing their understanding of the shape's specific attributes.

7. Measurement and Comparison Activities

Measurement and comparison activities introduce first graders to the fundamental concepts of size, length, weight, and capacity. These hands-on math problems for 1st graders focus on direct comparison and the use of non-standard units, teaching children that measurement is about quantifying attributes of objects. This skill builds spatial awareness and lays the groundwork for understanding standard units like inches and centimeters later on.

Students learn to describe the world around them using comparative language. For example, they might be asked, "Which is longer, your crayon or your pencil?" or "How many paperclips long is your book?" This approach connects abstract mathematical ideas to the tangible, everyday objects in their environment, making learning both intuitive and relevant.

Strategic Breakdown

• Direct Comparison First: The initial step is always direct comparison. Students physically place two objects side-by-side to determine which is taller, shorter, or longer. This concrete action solidifies the concept before introducing any form of unit.
• Introduce Non-Standard Units: Once direct comparison is mastered, introduce non-standard units like paperclips, blocks, or hand spans. The key is consistency; using the same unit (e.g., blocks) to measure multiple objects helps students understand that measurement requires a uniform tool.
• Focus on Attributes: Explicitly teach the language associated with different measurable attributes. Use words like length (long/short), height (tall/short), weight (heavy/light), and capacity (holds more/holds less) to build a precise mathematical vocabulary.

Actionable Tips for Practice

To make measurement meaningful, focus on exploration and real-world application.

• Measurement Hunts: Send children on a "measurement hunt" around the room. Ask them to find an object that is "shorter than their pencil" or "about 5 blocks long." This turns practice into an engaging game.
• Ordering Activities: Provide a set of objects of varying lengths, like straws or strips of paper, and have students arrange them from shortest to longest. This reinforces their understanding of relative size.
• Balance Scale Exploration: Use a simple balance scale to compare the weights of different classroom items. Ask predictive questions like, "Which do you think is heavier, the eraser or the glue stick?" to encourage critical thinking.

8. Multi-Step and Real-World Problem Solving

Multi-step and real-world problems are advanced math problems for 1st graders that challenge them to apply several skills within a single, relatable scenario. Instead of a straightforward calculation, these problems require students to think critically, sequence actions, and decide which operations to use. This mirrors how math is used in everyday life, building perseverance and deeper comprehension.

These problems often blend addition and subtraction. For example: "Sarah has 5 red apples and 3 green apples. She gives 2 apples to her friend. How many apples does Sarah have now?" This contextualized format helps students understand that math is a tool for answering questions about the world around them, moving beyond abstract numbers.

Strategic Breakdown

• Deconstruct the Problem: Teach students to break down the story into parts. In the example, the first step is finding the total number of apples (5 + 3 = 8), and the second step is subtracting the apples given away (8 - 2 = 6).
• Identify Key Information: Help children highlight or circle the important numbers and key action words (like "and," "gives away," "how many left"). This trains them to filter out irrelevant details and focus on what is needed to solve the problem.
• Visualize the Steps: Encourage drawing or modeling each part of the problem. A student might draw 8 apples first, then cross out 2. This visual representation makes the abstract process concrete and verifiable.

Actionable Tips for Practice

To develop strong real-world problem-solving skills, focus on process over speed.

• Act It Out: Use students and classroom objects to physically act out the story problem. This kinesthetic approach helps solidify the sequence of events and the corresponding mathematical operations.
• Questioning and Discussion: Guide students with questions like, "What do we know first?" and "What is the question asking us to find?" Allowing them to discuss their strategies with peers reinforces that there can be multiple ways to find the correct answer.
• Use Sentence Frames: Provide structured sentences to help students explain their thinking, such as: "First, I _______ because _______. Then, I _______ to find the answer."

These problems are essential for building a flexible and resilient mathematical mindset. By learning to navigate complex scenarios, students develop the skills needed for more advanced challenges. For more guidance on this process, you can find help with how to solve math problems step-by-step to build a solid foundation.

8-Point Comparison: 1st-Grade Math Problem Types

Example	Implementation complexity	Resource requirements	Expected outcomes	Ideal use cases	Key advantages
Simple Addition Problems (Within 10)	Low	Low — manipulatives, drawings, fingers	Basic addition fluency to 10; number sense; commutativity introduction	Intro to addition, small-group practice, early lessons	Easy to visualize and measure progress; engaging
Subtraction Through Removal and Comparison	Low–Medium	Moderate — manipulatives, comparison visuals	Understand subtraction as removal and difference; link to addition	Teaching subtraction concepts, correcting misconceptions	Concrete models; multiple strategies; real-world contexts
Number Sense and Counting Activities	Low–Medium	Low — counters, number lines, songs, apps	Improved counting, subitizing, sequencing, mental math foundation	Daily routines, warm-ups, intervention, early screening	Strong foundation for all arithmetic; versatile practice
Comparison Word Problems	Medium	Moderate — side-by-side objects, comparison bars, visuals	Relational thinking; comparison vocabulary; prep for difference problems	Lessons on "more/less" and relational language, transition to subtraction	Real-world relevance; supports inequality concepts
Place Value with Tens and Ones	Medium–High	Moderate–High — ten-frames, base-ten blocks, bundles	Understand positional value; decompose numbers; readiness for multi-digit work	Moving beyond 10, teaching regrouping and multi-digit arithmetic	Concrete grasp of abstract place value; supports mental strategies
Basic Geometry and Shape Identification	Low	Low — shape cutouts, real objects, sorting mats	Identify and describe 2D/3D shapes; develop spatial reasoning	Visual/spatial lessons, cross-curricular activities, shape hunts	Highly engaging; abundant real-world examples; low-cost
Measurement and Comparison Activities	Low–Medium	Low — non-standard units, classroom items, space	Understand comparison, ordering, non-standard measurement concepts	Hands-on measurement lessons before standard units; exploratory learning	Concrete, sensory experiences; integrates with other topics
Multi-Step and Real-World Problem Solving	High	Moderate — contextual materials, time for discussion and modeling	Higher-order reasoning, application of multiple skills, perseverance	Project-based tasks, assessment of understanding, mixed-skill practice	Promotes deep understanding, multiple solution strategies, motivation

Key Takeaways and Next Steps for Math Mastery

Navigating the world of first-grade mathematics is a foundational journey that sets the stage for all future learning. The diverse set of math problems for 1st graders we've explored, from simple addition to multi-step real-world scenarios, are not just about finding the right answer. They are about building a flexible, resilient, and deeply conceptual understanding of numbers and how they work in the world around us.

The core principle underpinning all these activities is that math should be tangible, relatable, and engaging. A first grader's mind thrives on connection. By grounding abstract concepts like place value in hands-on activities with blocks, or turning subtraction into a story about sharing snacks, we transform rote memorization into meaningful discovery. This approach ensures that students don't just know that 5 + 3 = 8; they understand what that equation represents.

Strategic Summary: From Problems to Principles

Let's distill the key strategies discussed throughout this article into actionable principles. Moving forward, prioritize these approaches to foster a robust mathematical mindset in your young learner.

• Make it Concrete: Always start with physical manipulatives. Whether using counting bears, base-ten blocks, or simple household items like buttons, tangible objects bridge the gap between abstract numbers and concrete reality. This is critical for building a solid foundation in addition, subtraction, and place value.
• Embrace Storytelling: Word problems are often the first major hurdle for young learners. The most effective strategy is to turn them into engaging narratives. Encourage students to draw pictures, act out the scenario, or retell the problem in their own words to ensure they grasp the "what" and "why" before tackling the "how."
• Focus on Number Sense: True mathematical fluency isn't about speed; it's about flexibility. Activities centered on counting, comparing numbers (greater than, less than), and understanding place value are essential. These skills empower students to see relationships between numbers, which is far more valuable than just memorizing facts.

Strategic Insight: The goal is not to create a human calculator but to nurture a curious problem-solver. Celebrate different solution paths and encourage students to explain their thinking. When a child can articulate why they grouped tens together or how they knew to subtract, they are demonstrating true conceptual mastery.

Actionable Next Steps for Continued Growth

With these foundational principles in mind, you can continue to support your first grader’s mathematical journey. The key is consistent, low-pressure practice that feels more like play than work.

1. Integrate Math into Daily Routines: Ask your child to help count items at the grocery store, measure ingredients while cooking, or identify shapes on a walk around the neighborhood. These small, consistent interactions reinforce concepts in a natural, stress-free context.
2. Vary the Problem Types: Avoid getting stuck on one type of problem. Mix and match addition, subtraction, measurement, and geometry. This variety keeps things interesting and helps students become more adaptable thinkers, ready to apply the right strategy to any challenge.
3. Encourage Productive Struggle: It is okay for a problem to be challenging. Instead of giving the answer away, ask guiding questions like, "What have you tried so far?" or "Can you draw a picture of the problem?" This builds resilience and teaches students that they are capable of working through difficulties.

Mastering the variety of math problems for 1st graders is a significant milestone. It equips them with the confidence and the core skills needed to tackle the more complex challenges of second grade and beyond, laying the groundwork for a lifetime of logical thinking and quantitative reasoning.

---

When a tricky word problem or a new concept leaves your student feeling stuck, getting instant, step-by-step help can make all the difference. Upload a photo of any math problem to Feen AI and receive clear, guided explanations to build understanding and independence. Visit Feen AI to empower your learner with on-demand support.