What is the pythagorean theorem? A Clear Visual Guide

The Pythagorean theorem is one of the most famous and useful principles in all of geometry. At its heart, it describes a special relationship found only in right-angled triangles. It states that the square of the longest side is equal to the sum of the squares of the other two sides.

This simple but powerful idea is captured in the classic formula: a² + b² = c².

Your Quick Answer to the Pythagorean Theorem

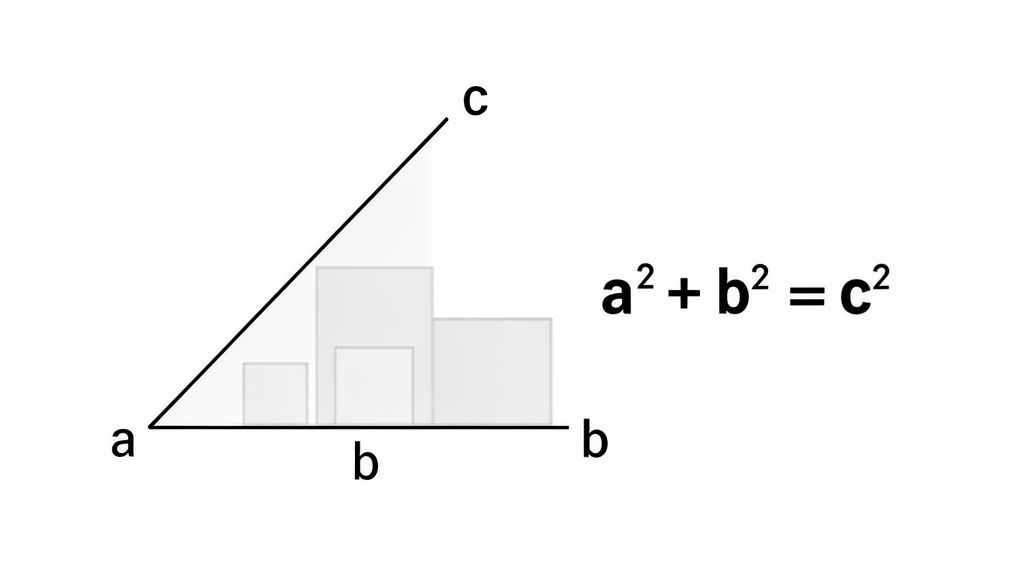
Let's cut right to it. The Pythagorean theorem is your go-to tool for finding a missing side length on any right-angled triangle, as long as you know the other two.

Think of it this way: imagine drawing a square on each of the triangle's three sides. The theorem reveals a fascinating truth—the area of the two smaller squares (built on the shorter sides) perfectly adds up to the area of the largest square (built on the longest side).

It’s this elegant relationship that gives us the unforgettable formula a² + b² = c². Grasping this core concept is the first real step to tackling everything from textbook problems to practical, real-world challenges.

The Core Components of the Theorem

Before you can use the formula, you have to know what you’re looking at. Identifying the parts of a right-angled triangle correctly is the most important step, and mixing them up is where most people go wrong.

Here's the breakdown of what each variable means:

• a and b (The Legs): These are the two sides that meet to form the 90-degree right angle. It doesn't matter which one you call 'a' and which you call 'b'.
• c (The Hypotenuse): This is always the longest side. An easy way to spot it is that it’s directly opposite the right angle.

Getting this foundation right will give you the confidence to start solving problems immediately. With these basics down, you’re ready to see how this ancient rule works in practice.

The objective in mathematics is not to obtain the highest score, but to increase understanding. The Pythagorean theorem is a perfect example—a concept that builds a foundation for deeper mathematical and scientific exploration.

Breaking Down the Formula a² + b² = c²

To make it even clearer, here’s a quick reference guide for what each part of the formula represents on the triangle.

Variable	Triangle Part	Key Characteristic
a	Leg	One of the two sides that form the right angle.
b	Leg	The other side that forms the right angle.
c	Hypotenuse	Always the longest side, located opposite the right angle.

Keep this table in mind as you work through examples. It’s a simple cheat sheet that will help you set up your equations correctly every time.

The Secret History of the World's Most Famous Theorem

The name "Pythagorean theorem" is a bit of a misnomer. While the Greek philosopher Pythagoras gets all the credit, the truth is this powerful formula has a history that’s far older and more tangled than most people think. It wasn't a sudden flash of genius in ancient Greece. Its real story begins thousands of years earlier, in the fertile crescent, where ancient civilizations were already using it to build their world.

Way before Pythagoras of Samos was even born, builders and surveyors in ancient Babylon had a problem to solve: how to create perfect 90-degree angles and measure land with precision. They figured out the special relationship between the sides of a right-angled triangle and turned it into a fundamental tool. This wasn't some abstract idea; it was working technology, essential for everything from mapping out farmland to constructing buildings.

This practical know-how shows that the core concept of what is the Pythagorean theorem was an idea shared across cultures, long before it ever got a formal name.

A Story Etched in Clay

The most incredible evidence we have for this comes from a small, unassuming clay tablet. It’s called Plimpton 322, and it was created in ancient Babylon around 1800 BCE—that’s over a thousand years before Pythagoras walked the Earth.

This little tablet is basically a cheat sheet for ancient architects. It lists 15 sets of "Pythagorean triples," which are neat sets of whole numbers (like the famous 3-4-5 combo) that perfectly fit the a² + b² = c² formula. It wasn't just simple stuff, either. The tablet includes complex sets with numbers as large as 119 and 169, proving a sophisticated understanding of the math involved.

This ancient record completely changes the story. It shows the theorem wasn't discovered by one man, but was a shared piece of knowledge that grew and evolved over centuries. You can dig deeper into this fascinating history on Wikipedia.

Plimpton 322 is a powerful reminder that math often grows from practical needs. What we learn as a formula in a classroom was once a vital tool for building entire civilizations.

So, Why Does Pythagoras Get All the Credit?

If the Babylonians (and probably others, like the Egyptians and Chinese) were using this rule for centuries, why is Pythagoras’s name attached to it? The answer comes down to the difference between using a tool and proving why it works.

Earlier cultures knew that it worked. They used it as a reliable rule of thumb. But Pythagoras and his followers are credited with being the first to formally prove it as a universal law of mathematics.

Their contribution was a game-changer for a few key reasons:

• They Proved It: They built a logical, step-by-step argument showing the theorem was true for every single right-angled triangle, not just a few specific examples.
• They Made It Abstract: They elevated the idea from a builder's trick to a fundamental principle of geometry.
• They Taught It: The Pythagorean school was hugely influential. They documented their work and taught it to others, which is how the theorem survived and spread through the ancient world.

So, while Pythagoras didn't invent the rule, he and his school were the ones who explained why it works, cementing its place as a cornerstone of mathematics. That shift from a handy trick to a timeless, proven theorem is why his name is the one we remember today.

How We Know the Theorem Actually Works

It's one thing to memorize the formula a² + b² = c², but how can we be sure it holds true for every single right-angled triangle out there? The answer is a mathematical proof—a rock-solid line of reasoning that shows this relationship isn't just a happy accident but a universal truth.

And the best part? You don't need a Ph.D. in mathematics to follow along. Some of the most convincing proofs are surprisingly simple and visual.

The real beauty of the Pythagorean theorem lies in its journey. It started with practical observations etched into ancient clay tablets, became a vital tool for surveyors, and eventually blossomed into the abstract proofs that form the bedrock of modern geometry.

This journey from simple record-keeping to practical surveying laid the groundwork for incredible engineering feats, like the construction of the great pyramids.

Seeing is Believing: A Visual Proof

One of the most intuitive ways to understand the theorem is to literally see it in action. This method, often called a "proof by rearrangement," needs no complicated algebra, just a little bit of creative geometry.

First, picture a right-angled triangle. Now, imagine building a large square where each side is as long as the two legs combined (a + b). If you arrange four identical copies of your triangle in the corners of this large square, what do you get in the middle? You're left with a smaller, tilted square whose sides are each the length of the hypotenuse, c.

The area of that middle square is simply c².

By just moving shapes around, we can physically see the connection between the areas of the squares on the legs and the square on the hypotenuse. It makes the abstract formula feel real and much easier to trust.

Now for the magic trick. Let’s rearrange those same four triangles inside the big square. If we slide them around to form two rectangles, the empty space that's left over is now split into two separate squares: one with an area of a² and another with an area of b².

Since we started with the same big square and the same four triangles, the leftover empty space has to be the same in both arrangements. That means the single c² square from our first setup has the exact same area as the a² and b² squares combined. And just like that, you’ve proven a² + b² = c².

Proving It With Logic: An Algebraic Approach

Visual proofs are fantastic, but an algebraic proof offers a different kind of certainty. It uses the pure logic of equations to build a case that works no matter what numbers you use for the sides.

A classic algebraic proof starts with the same setup as our visual one: a large square with side length (a + b) holding our four right triangles and the central c² square.

We can describe the total area of this big square in two different ways:

1. As one large square: The area is its side length squared, or (a + b)². If you expand that, you get a² + 2ab + b².
2. As the sum of its parts: The area is also the sum of the four triangles plus the inner square. The area of one triangle is ½(ab), so four of them make 2ab. Add the inner square's area, and you get a total of 2ab + c².

Because both expressions represent the exact same area, they must be equal.

So, we can set them equal to each other: a² + 2ab + b² = 2ab + c².

Now, just subtract 2ab from both sides. What you’re left with is that famous, elegant conclusion: a² + b² = c².

A Theorem With Hundreds of Proofs

What makes the Pythagorean theorem so special is how many different ways it can be proven. We're not talking about a handful—there are literally hundreds of unique proofs, each offering a slightly different angle on this fundamental truth.

This journey of discovery has unfolded over thousands of years and across countless cultures. The first printed edition of Euclid's Elements, which contained a key proof, appeared in Venice in 1482 CE, spreading the theorem's power across Europe. While Euclid's own proof dates back to around 300 BCE, brilliant minds from ancient Greece to the Arab world and the Renaissance—including Leonardo da Vinci—have all added their own.

By 2026, the official count of unique proofs is expected to pass 300. It even includes a clever proof using trapezoids developed in 1876 by James Garfield, right before he became President of the United States. You can dig into a detailed timeline of these mathematical milestones to appreciate its incredible history.

Solving Problems with the Pythagorean Theorem

Knowing the formula is one thing, but the real magic happens when you start using it to solve actual problems. This is where the abstract equation a² + b² = c² becomes a practical tool for figuring out real-world distances.

The process is surprisingly straightforward. Once you get the hang of it, you'll see how any geometric puzzle involving a right triangle can be turned into a simple algebra problem. Let's walk through a few examples to see it in action.

Finding the Hypotenuse When You Know the Legs

The most common application of the theorem is finding the hypotenuse (c) when you already know the lengths of the two shorter sides, the legs (a and b). This is the formula in its most direct form.

Imagine a right triangle with one leg measuring 3 inches and the other 4 inches. Your job is to find the length of the longest side—the hypotenuse.

Here’s how to break it down:

1. Start with the formula: Always begin with the foundation: a² + b² = c².
2. Plug in the numbers: Substitute the leg lengths for a and b. The equation becomes 3² + 4² = c².
3. Square the values: Calculate the square of each leg, which gives you 9 + 16 = c².
4. Add them up: Combine the two results. Now you have 25 = c².
5. Find the square root: To solve for c, just take the square root of 25. The answer is 5.

So, the hypotenuse is 5 inches long. This classic 3-4-5 triangle is a perfect example of a Pythagorean triple, where all three sides are neat whole numbers.

Finding a Missing Leg When You Know the Hypotenuse

But what if the situation is flipped? What if you know the length of the longest side and just one of the shorter sides? This requires a small tweak to the formula, but the logic is the same. It’s like solving the puzzle in reverse.

Let’s say you’re measuring a TV. You know the diagonal (the hypotenuse) is 13 inches and the height (one leg) is 5 inches. How do you find the TV's width (the other leg)?

The key here is to isolate the side you don't know. Instead of adding the squares, you'll end up subtracting. This simple change is all it takes to solve for a missing leg.

Let's walk through the steps:

• Start with the formula: As always, it's a² + b² = c².
• Substitute known values: We'll say a = 5 and c = 13. Our equation is now 5² + b² = 13².
• Calculate the squares: This turns the equation into 25 + b² = 169.
• Isolate the unknown (b²): To get b² by itself, subtract 25 from both sides: 169 - 25 = 144. So, b² = 144.
• Take the square root: The square root of 144 is 12.

The width of the TV screen is 12 inches. This shows how a minor algebraic adjustment makes the theorem incredibly versatile. If you're tackling more complex numbers or just want to check your work, an AI math solver can walk you through the steps.

Tackling a Real-World Word Problem

Now, let's apply these skills to a practical scenario. This is where you really see the theorem jump off the page and into the real world.

Problem: You're using a 15-foot ladder. For it to be stable, you need to place the base of the ladder 9 feet away from the wall. How high up the wall will the ladder actually reach?

1. Picture the triangle: The ladder, the wall, and the ground form a perfect right triangle.
2. Assign the sides: The ladder is the longest side, so it's our hypotenuse (c = 15). The distance from the wall is one of the legs (a = 9). The height on the wall is the leg we need to find (b).
3. Set up the equation: Using a² + b² = c², we get 9² + b² = 15².
4. Solve for b:
   • Square the numbers you know: 81 + b² = 225.
   • Subtract 81 from both sides: b² = 225 - 81.
   • Do the subtraction: b² = 144.
   • Find the square root: b = 12.

The ladder will reach 12 feet up the wall. Getting comfortable with applying mathematical rules to real-life situations is a great way to improve problem solving skills. By following this simple, structured approach, you can confidently solve any problem that involves a right triangle.

Putting the Theorem to Work in the Real World

It’s tempting to file the Pythagorean theorem away as just another formula you have to memorize for a test. You might even be asking yourself, "When am I ever going to use this?" The truth is, you already do. This ancient mathematical gem is constantly working behind the scenes in the world all around you.

From the home you live in to the smartphone in your pocket, the theorem is a fundamental tool for professionals in a huge range of fields. It's not just some abstract idea—it’s a hands-on problem-solver that helps people build, create, and find their way with incredible precision.

Let's look at a few examples of how this formula jumps off the textbook page and into our everyday lives.

Building a Square and Level World

Ever wonder how construction crews ensure the corners of a new building are perfect 90-degree angles? They aren't just guessing. They're often using a brilliantly simple trick based on the theorem, known as the 3-4-5 rule.

This method is a real-world application of a Pythagorean triple. A builder can measure 3 feet from a corner along one wall and 4 feet from the same corner along the other wall. If that corner is truly "square," the diagonal line connecting those two points has to be exactly 5 feet. Why? Because 3² + 4² = 5².

If that diagonal measures anything other than 5 feet, they know the corner isn't a true right angle and needs adjusting. This quick check is what guarantees that foundations are solid, walls stand straight, and the entire structure is safe and stable.

The 3-4-5 rule is a cornerstone of construction and carpentry. It’s a low-tech, high-accuracy method that has been trusted for centuries to get things right on projects of every size.

Navigating with Your Smartphone

Anytime you pull up a map on your phone to get directions, you're tapping into the power of the Pythagorean theorem. GPS technology pinpoints your location by triangulating signals from satellites orbiting the Earth.

Imagine the map on your screen is a giant grid. Your location is one coordinate point, and your destination is another. The shortest distance between you and your destination—the "as the crow flies" path—is just the hypotenuse of a giant, invisible right triangle.

The two legs of that triangle are:

• The distance east or west you need to travel.
• The distance north or south you need to travel.

GPS software squares those two distances, adds them up, and finds the square root in a fraction of a second. This calculation gives you the most direct route and is a core part of the distance formula used in coordinate geometry—which is really just the Pythagorean theorem in a different outfit.

Designing Digital Worlds and Video Games

The theorem’s influence doesn't stop at the physical world; it’s a crucial building block for the digital spaces we love. Video game developers rely on it constantly to manage everything from character movement to the physics of a virtual environment.

For instance, when a character runs diagonally across the screen, the game engine has to calculate the total distance they've traveled. If the character moves 8 pixels horizontally and 6 pixels vertically in a single frame, the theorem tells us the actual distance covered is 10 pixels (8² + 6² = 100, and the square root of 100 is 10).

This simple calculation is essential for:

• Collision Detection: Figuring out if a character is about to run into a wall.
• AI Movement: Helping non-player characters (NPCs) find the most efficient path to their target.
• Physics Simulation: Calculating the arc of a thrown grenade or the force of an impact.

The theorem's logic also appears in countless physics calculations, from mechanics to electromagnetism. For a closer look at the math that underpins our physical reality, this physics formulas cheat sheet is a great resource. From building houses to building virtual worlds, this seemingly simple formula proves its worth over and over again.

Common Mistakes and How to Avoid Them

The Pythagorean theorem looks straightforward on the surface, but a few common tripwires can easily lead you down the wrong path. Getting familiar with these pitfalls is the best way to build your confidence and make sure you get it right, every time.

One of the biggest mistakes I see students make is mixing up the sides of the triangle. The formula a² + b² = c² is completely dependent on 'c' being the hypotenuse—that's the longest side, the one sitting directly opposite the right angle. If you accidentally plug one of the shorter legs into the 'c' spot, your answer will be way off. It just won't make sense.

So, how do you avoid this? Simple. Before you write down a single number, find the hypotenuse. It's the only side that doesn't touch the little square marking the 90-degree angle. Label it 'c' immediately. Then you can label the other two 'a' and 'b'. That one little habit will save you a world of trouble.

Forgetting Key Calculation Steps

The other place where things often go sideways is in the calculation itself. It's so easy to get ahead of yourself and forget the two most critical operations: squaring the numbers at the start and taking the square root at the very end. These aren't just minor details; they are the entire engine of the theorem.

The goal in math isn't just about getting the right answer. It’s about understanding why it's the right answer. Spotting these common errors helps you learn the logic behind the formula, not just memorize the steps.

Let's look at a classic 6-8-10 triangle where we're trying to find the hypotenuse, and see how easy it is to go wrong.

• Wrong Way (Forgetting to Square): 6 + 8 = c, so c = 14. This is a classic mix-up. The formula is about the squares of the lengths, not the lengths themselves.
• Right Way: 6² + 8² = c², which turns into 36 + 64 = c², giving us 100 = c².

Now, here comes the second part of the trap. After getting 100, it's tempting to stop and call it a day. But you're not done yet! You've found c², not c. This is probably the single most common error: forgetting the final square root.

• Wrong Way (Forgetting the Square Root): c² = 100, so c = 100. This is incorrect. You've found the area of the square built on the hypotenuse, not the length of the side itself.
• Right Way: If c² = 100, then you have to take the square root of both sides. That gives you c = √100, which means c = 10.

The best defense against these mistakes is a consistent, step-by-step process. Treat it like a checklist for every problem. If you want to build stronger problem-solving habits, our guide on how to solve math problems step-by-step can help you create a solid routine.

Got Questions? We've Got Answers

Once you've wrapped your head around the basics, a few common questions tend to pop up. Let's dig into them to clear up any lingering confusion and see how this theorem fits into the wider world of math.

Does This Theorem Work for Any Triangle?

This is a big one, and the answer is a firm no. The Pythagorean theorem is a specialist—it only works for right-angled triangles. That perfect 90-degree corner is the magic ingredient that makes the a² + b² = c² relationship hold true.

If you're dealing with a triangle that doesn't have a right angle (what we call acute or obtuse triangles), you'll need to reach for different tools. That's where things like the Law of Sines and the Law of Cosines come into play. The theorem's real power lies in its specificity.

What's a Pythagorean Triple?

Think of a Pythagorean triple as a perfect, whole-number solution to the theorem. It’s a set of three positive integers—like 3, 4, and 5—that fit the a² + b² = c² equation exactly. They're awesome little shortcuts that save you from having to do the math every time.

Knowing these triples is like having a cheat sheet for geometry. Spot one in a problem, and you can instantly solve for a missing side without even touching a calculator. It's a huge time-saver on homework and tests.

Here are a few of the most common families:

• 3, 4, 5 (because 3² + 4² = 9 + 16 = 25, which is 5²)
• 5, 12, 13 (because 5² + 12² = 25 + 144 = 169, which is 13²)
• 8, 15, 17 (because 8² + 15² = 64 + 225 = 289, which is 17²)

What’s really cool is that any multiple of a triple is also a triple. So, if you see a triangle with legs of 6 and 8, you can recognize it's just a 3-4-5 triangle scaled by 2, meaning the hypotenuse must be 10.

How Does This Help Me Find Distances on a Map?

Ever wondered how Google Maps calculates the straight-line distance from your house to your school? You're looking at the Pythagorean theorem in action. It’s the engine behind the Distance Formula used in coordinate geometry.

Picture any two points on a grid. You can find the distance between them by drawing an imaginary right triangle.

• The horizontal distance between the points becomes one leg (a).
• The vertical distance becomes the other leg (b).
• The direct, straight-line path between them is the hypotenuse (c).

GPS devices and mapping apps are constantly using this principle—a² + b² = c²—to calculate the shortest path between two coordinates. It's one of the most practical, real-world applications of the theorem.

---

Struggling with homework or need clearer explanations for tough math problems? Feen AI is an AI-powered helper that gives you instant, step-by-step solutions and clear insights across subjects like math, physics, and chemistry. Just upload a picture of your problem and get the help you need to succeed. Try it now at https://feen.ai.