How to Factor Polynomials Completely

Factoring any polynomial can feel like staring at a complex puzzle, but there’s a secret weapon that makes every problem simpler: always start by finding the Greatest Common Factor (GCF). This isn't just a helpful tip; it's the foundational first move that unlocks the rest of the solution.

Once you pull out the GCF, the polynomial left behind is cleaner and much easier to work with. From there, you can quickly spot the right pattern—like a Difference of Squares or a simple trinomial—and finish the job. Nailing this GCF-first approach is what separates struggling students from those who can break down any expression with confidence.

Your Starting Point for Factoring Any Polynomial

Think of the GCF as building the frame of a jigsaw puzzle. You wouldn't just start grabbing random pieces from the middle, right? You’d find all the straight-edged border pieces first. Factoring out the GCF does the same thing—it creates structure and simplifies the entire picture, setting you up for a much smoother process.

So many students make the classic mistake of jumping straight into more advanced factoring methods. They'll try to tackle a complicated trinomial with large coefficients, completely missing the fact that a common factor could have made all the numbers smaller and the patterns more obvious. This almost always leads to frustration and mistakes.

Why The GCF Is Non-Negotiable

Pulling out the GCF isn't just about neatness; it fundamentally changes the problem. Take an expression like 12x³ – 27x. At first glance, it looks a bit messy.

But as soon as you spot the GCF of 3x, you can rewrite it as 3x(4x² – 9).

Instantly, the problem transforms. What's left inside the parentheses, 4x² – 9, is a perfect Difference of Squares, which is simple to factor. Without that first GCF step, you might have missed it entirely. This is a core part of developing a reliable system for math, which you can read more about in our guide on how to solve math problems step-by-step.

Pro Tip: Get into the habit of checking for a GCF every single time. It might just be a number, or it might be a single variable, but making it a reflex will save you countless headaches and help you see the true structure of the polynomial.

This visual decision tree lays out the exact path to follow when you're learning how to factor polynomials completely.

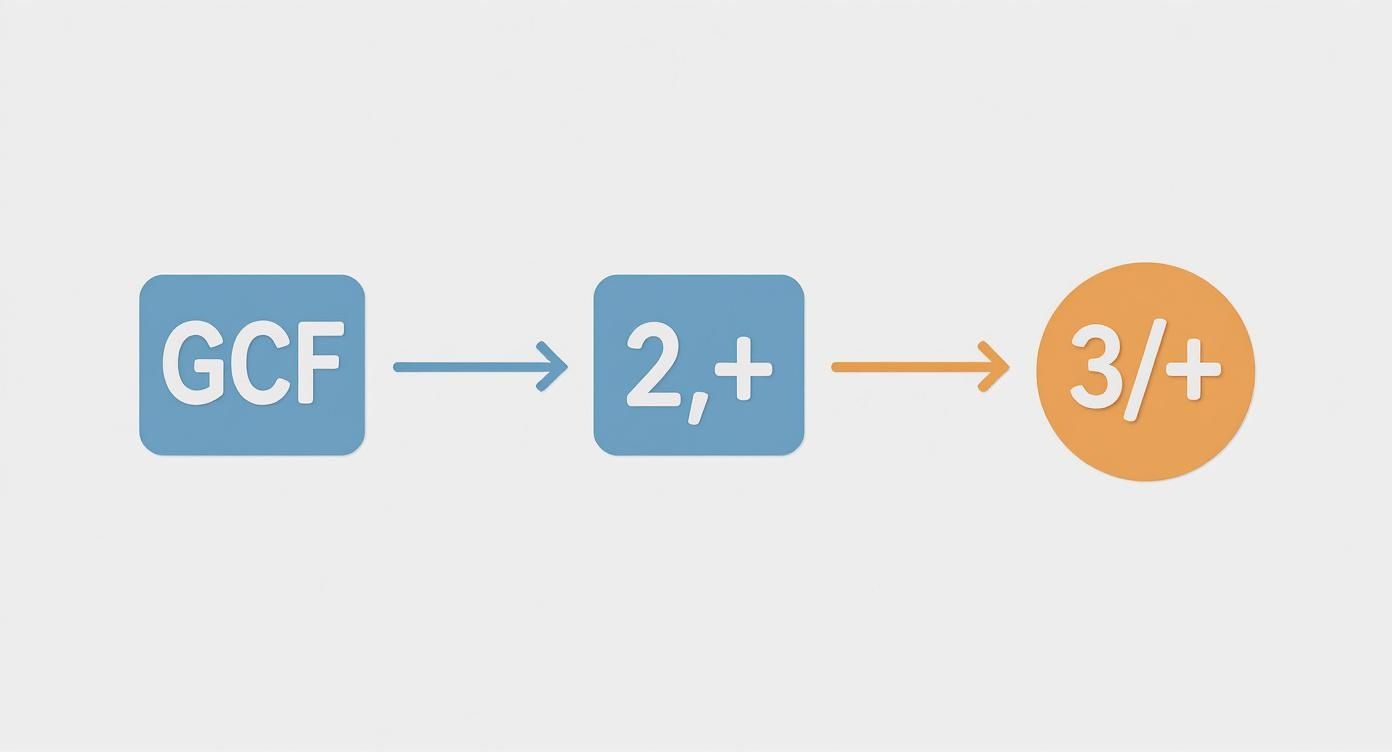
As the flowchart shows, everything starts with the GCF. After that, your next move is determined by how many terms are left.

Building Your Factoring Strategy

After you’ve pulled out the GCF, your strategy is dictated by what remains. Just count the terms in the polynomial inside the parentheses—that's your clue for which method to use next.

I've put together a quick reference table that I call the "Factoring Decision Flowchart." It's the mental checklist I run through every time I see a new polynomial.

The Factoring Decision Flowchart

Number of Terms	Recommended First Method to Try	Example Structure
Two Terms	Check for special patterns	Difference of Squares: a² - b² Sum/Difference of Cubes: a³ ± b³
Three Terms	Standard trinomial factoring	Quadratic Trinomial: ax² + bx + c
Four+ Terms	Factoring by Grouping	Grouping: ax + ay + bx + by

This table maps out your next steps perfectly. A binomial (two terms) almost always points to one of the special factoring patterns. A trinomial (three terms) means you’re likely dealing with a quadratic you can un-FOIL. And if you see four or more terms, your best bet is to try factoring by grouping.

By following this GCF-first approach and then counting the terms, you'll have a clear, reliable game plan for any polynomial that comes your way.

Mastering the Essential Factoring Techniques

Once you’ve pulled out the Greatest Common Factor, the polynomial left behind tells you what to do next. The number of terms and their structure are your roadmap, pointing you toward the right factoring technique. Think of these methods as specialized tools in your algebra kit, each one perfect for a specific type of problem.

Learning to spot these patterns is what transforms factoring from a frustrating chore into a satisfying puzzle. We'll walk through the most common methods you'll use day-to-day, starting with four-term polynomials before moving on to those familiar trinomials and binomials.

Strategic Pairing with Factoring by Grouping

When a polynomial with four terms lands on your desk, your first instinct should be factoring by grouping. This method can feel a bit like a magic trick. You strategically pair up terms to uncover a hidden common factor that wasn't obvious at first. It’s all about creating order from what initially looks like chaos.

Let's see it in action with this polynomial: x³ + 5x² + 2x + 10.

Right away, we can see there’s no GCF for all four terms, so grouping is our next move. The trick is to split the polynomial into two pairs and find the GCF for each one.

• Pair 1: x³ + 5x²
• Pair 2: 2x + 10

Now, let's factor the GCF out of each binomial. From the first pair, we can pull out x², leaving us with x²(x + 5). From the second pair, we can pull out a 2, which gives us 2(x + 5).

This is the make-or-break moment. Look closely: both results share the exact same binomial factor, (x + 5). That's what we were hoping for! If you don't get a common binomial at this stage, it often means you need to go back and rearrange the original terms into different pairs.

Since (x + 5) is now a common factor, we can pull it out, treating it like a single unit. The leftovers, x² and +2, come together to form the second factor. This gives us our final answer: (x + 5)(x² + 2).

Tackling Trinomials with Precision

Trinomials, especially those in the form ax² + bx + c, are probably the most common polynomials you'll ever have to factor. The goal is to work backward from the FOIL method to find the two binomials that multiply together to create the original trinomial. Your strategy will shift slightly depending on whether 'a' is 1 or a larger number.

When a = 1 (like in x² + 7x + 12), the process is pretty straightforward. You're just hunting for two numbers that do two things at once:

1. Multiply to get the constant term 'c' (which is 12).
2. Add up to the middle coefficient 'b' (which is 7).

After a moment's thought, you’ll land on 3 and 4. They work perfectly (3 × 4 = 12 and 3 + 4 = 7). These two numbers become the constants in your binomials: (x + 3)(x + 4).

When a ≠ 1, the puzzle gets a bit more involved, but the core logic is the same. This is where you might use trial-and-error or the "AC method." With trial-and-error, you're just systematically testing combinations of factors for the 'a' and 'c' terms until you land on the pair that gives you the correct middle term, 'b'.

Powerful Shortcuts with Special Patterns

Some polynomials have a distinct structure that lets you factor them instantly, skipping the longer methods entirely. Recognizing these patterns is a huge time-saver and a critical skill if you want to know how to factor polynomials completely. These shortcuts aren't new; the mission to solve polynomial equations has been a central part of algebra for thousands of years. In fact, the earliest evidence dates back almost 3,000 years to Babylonian tablets from 1900 BC that show work on quadratic equations. You can explore the fascinating history of polynomial factoring on MathProjectASP to see how these ideas grew over the centuries.

Here are the three must-know special patterns:

• Difference of Squares: a² – b² = (a – b)(a + b) Any time you see one perfect square being subtracted from another, this is your shortcut. For example, 9x² – 25 factors into (3x – 5)(3x + 5) because 9x² is just (3x)² and 25 is 5².

• Difference of Cubes: a³ – b³ = (a – b)(a² + ab + b²) This pattern works for one perfect cube subtracted from another. For x³ – 64, where a = x and b = 4, the factored form is (x – 4)(x² + 4x + 16).

• Sum of Cubes: a³ + b³ = (a + b)(a² – ab + b²) This is just like the difference of cubes, but with a different sign pattern. For 8y³ + 1, where a = 2y and b = 1, it factors to (2y + 1)(4y² – 2y + 1).

A Pro Tip for Cubes: Memorizing the Sum and Difference of Cubes formulas can feel tough, but I always tell my students to use the acronym SOAP. It stands for Same, Opposite, Always Positive. This little trick describes the signs in the longer trinomial factor. The first sign is the same as the original binomial, the second is the opposite, and the last one is always positive.

Getting comfortable with these core techniques—grouping, trinomial factoring, and special patterns—gives you a versatile toolkit for almost any polynomial. The real key is practice. The more problems you solve, the quicker you'll get at spotting which tool is the right one for the job.

The Secret to Factoring Polynomials Completely

When a test question says "factor completely," it’s not just a friendly suggestion. It’s the entire point of the problem. This is a signal that you’re likely looking at a multi-layered puzzle, not a simple one-and-done operation.

The real secret to mastering this is to stop thinking about finding one answer and start hunting for all of them. You have to keep breaking the expression down until every last piece is in its simplest, prime form. It's a cycle: you factor once, then you stare at your new factors and ask the most important question in algebra: "Can this be factored again?"

This habit of continuous checking is what separates students who know the formulas from those who truly master the skill. You might pull out a Greatest Common Factor (GCF) only to find a perfect Difference of Squares hiding inside. Or you might factor a trinomial and realize one of its binomial factors is actually a Difference of Cubes. Let's dig into what this multi-step approach looks like with a couple of real examples.

Thinking in Multiple Layers

Your first move should always be to look for a GCF. Always. But the most critical step is what comes after that. You have to see your result not as the finish line, but as a brand-new starting point.

Take a look at the polynomial 3x³ – 75x.

At first glance, that x³ term might tempt you to try something fancy, but the GCF rule is non-negotiable. The GCF for both terms here is 3x. Pulling it out to the front leaves you with:

3x(x² – 25)

This is where a lot of people stop, thinking the job is done. But a trained eye will immediately spot that the expression in the parentheses, x² – 25, is a classic Difference of Squares. It can be broken down even more.

• x² is a perfect square (it's x squared).
• 25 is a perfect square (it's 5 squared).

So, (x² – 25) factors neatly into (x – 5)(x + 5). To get your final, completely factored answer, you just bring down the original GCF you pulled out.

The complete factorization is 3x(x – 5)(x + 5). Each piece—3x, (x-5), and (x+5)—is now prime. Nothing else can be done. That’s what "completely" means.

Key Takeaway: Think of yourself as a detective. Finding the GCF is your first clue, but you have to follow that clue to solve the rest of the mystery. Always inspect every factor you create.

Combining Techniques for More Complex Problems

The real test of your factoring skills comes when problems force you to chain multiple techniques together. This is where pattern recognition becomes your best friend. You might have to use grouping, then a special pattern, or a GCF followed by trinomial factoring.

Let's walk through a more complex example that mixes a few ideas: 2x⁴ – 2.

1. Start with the GCF: The greatest common factor is just 2. Factoring it out instantly simplifies the problem. 2(x⁴ – 1)

2. Analyze What's Left: Now, just focus on x⁴ – 1. It might not look familiar at first, but it is a Difference of Squares! Think of it this way: a = x² and b = 1, because (x²)² = x⁴ and 1² = 1. Using the a² – b² = (a – b)(a + b) formula, we get: 2(x² – 1)(x² + 1)

3. Scan and Repeat: Hold on, we're not done yet. Look closely at the new factors. The term (x² + 1) is a Sum of Squares, which is prime and can't be factored further with real numbers. But look at (x² – 1)—it's another Difference of Squares! This time, a = x and b = 1. So, (x² – 1) breaks down into (x – 1)(x + 1).

4. Assemble the Final Answer: Finally, put all the prime pieces back together. The most common mistake here is forgetting that original GCF you pulled out in the very first step.

The completely factored form is 2(x – 1)(x + 1)(x² + 1).

This example is the perfect illustration of what "factor completely" really means. We had to apply the Difference of Squares formula twice in the same problem. If you can build the habit of re-evaluating your work after each step, you'll never leave a problem half-finished again.

Advanced Strategies for Tricky Polynomials

We’ve covered the go-to tools that will handle most of the polynomials you'll encounter. But what happens when you’re staring down a cubic or quartic expression that won't cooperate? No obvious special pattern, and factoring by grouping just isn't working.

This is where the real problem-solving begins. Think of these advanced methods as your plan B for those tougher polynomials that seem impossible at first glance. They give you a systematic way to find roots and crack open complex expressions, breaking them down into simpler, more manageable factors.

Finding Potential Roots with the Rational Root Theorem

When you're stuck with a high-degree polynomial like 2x³ + 3x² – 8x + 3 = 0, guessing where to start is a losing game. You need a better strategy.

This is where the Rational Root Theorem comes in. It's a lifesaver because it generates a complete list of all possible rational roots for the polynomial. No more random guessing.

Here's the idea:

• Find ‘p’, which is just all the integer factors of the constant term (the number without a variable). For our example, the constant is 3, so its factors are ±1 and ±3.
• Next, find ‘q’, which represents all the integer factors of the leading coefficient (the number on the highest-power term). Our leading coefficient is 2, so its factors are ±1 and ±2.

The potential rational roots are all the possible fractions you can make by putting p over q. For our polynomial, the list of possible roots is ±1/1, ±3/1, ±1/2, ±3/2.

Simplified, that gives us ±1, ±3, ±1/2, and ±3/2. Now we have a finite, manageable list to test instead of an infinite number of possibilities.

Testing Roots with Synthetic Division

Once you have that list of potential roots, you need a fast way to check them. Enter synthetic division. It's a slick, super-fast alternative to long division that will tell you if a number is a root and, if it is, what's left of the polynomial.

Let's test one of our potential roots, x = 1. If it's a true root, we should get a remainder of zero.

Running x = 1 through synthetic division gives us a remainder of 0. We've found one! This confirms two critical things:

1. x = 1 is a root of the polynomial.
2. Therefore, (x – 1) is a factor.

The result of the division also gives us the coefficients of the "depressed" polynomial: 2x² + 5x – 3. We’ve successfully broken our tough cubic down into (x – 1)(2x² + 5x – 3). That remaining quadratic is much easier to handle, and factoring it gives us our final answer: (x – 1)(2x – 1)(x + 3).

Factoring polynomials wasn't just invented for math class. Historically, it was a crucial skill for simplifying calculations, especially before calculators. It helped engineers and mathematicians find solutions to complex equations much faster. You can find out more about the history of these mathematical tools on YouTube.

Using Substitution for Quadratic-Like Polynomials

Sometimes you'll run into a polynomial that isn't a quadratic but sure does look like one. Take x⁴ + 5x² + 6, for example. It's a quartic, but notice the pattern of the exponents (4, 2, and 0). This structure is a dead giveaway that we can use a clever trick called u-substitution.

The goal here is to temporarily simplify the expression. Let's make a substitution: we'll set u = x².

By replacing every x² with u, our complicated quartic magically becomes a simple quadratic trinomial: u² + 5u + 6

Now that is something we know how to handle. We just need two numbers that multiply to 6 and add to 5, which are obviously 2 and 3. (u + 2)(u + 3)

But we're not quite done. The final, crucial step is to substitute x² back in for u: (x² + 2)(x² + 3)

Both of these factors are prime (they're a Sum of Squares), so our work is complete. This substitution trick is an elegant way to turn a complex problem into a familiar one, much like knowing how to solve systems of linear equations helps you untangle multiple variables at once. It’s all about turning overwhelming problems into a series of manageable steps.

Common Factoring Mistakes to Avoid

Learning to factor polynomials is a process, and believe me, everyone hits a few bumps along the way. Even after you've mastered the methods, tiny slip-ups can derail your entire problem. Getting familiar with these common pitfalls is the best way to steer clear of them and build solid, accurate habits.

One of the most frequent errors I see is students stopping too early. You might successfully pull out a GCF or factor a trinomial, but the job isn't done until every single factor is broken down as far as it can go. Always ask yourself, "Can this be factored again?"

Forgetting the GCF First

This is, without a doubt, the number one mistake I see students make. You’re faced with a big, complicated polynomial, and your first instinct is to jump into an advanced technique like grouping or the AC method. But ignoring the Greatest Common Factor (GCF) almost always makes the problem ten times harder than it needs to be.

Take 12x² + 36x + 24. A student might try to force the AC method right away, multiplying 12 × 24 to get a whopping 288. Then they’re stuck hunting for factors of 288 that add up to 36. That’s a fast track to frustration and calculation errors.

The Right Approach: The GCF here is 12. Once you pull that out, the expression simplifies to 12(x² + 3x + 2). Suddenly, that trinomial inside is a piece of cake to factor, giving you the final answer: 12(x + 1)(x + 2).

Mishandling Negative Signs

Negative signs are small but incredibly powerful. They’re a frequent culprit behind wrong answers, especially when you're factoring by grouping. A common slip-up happens when you factor a negative GCF from the second pair of terms but forget to change the sign of the second term inside the new parentheses.

Here’s what goes wrong: Factoring x³ – 5x² – 4x + 20

• Group it: (x³ – 5x²) + (–4x + 20)
• Pull out GCFs: x²(x – 5) – 4(x + 5) ← There's the mistake!

See how the binomials (x – 5) and (x + 5) don't match? When you factor out a –4 from +20, the result is –5. The correct step is x²(x – 5) – 4(x – 5), which gets you to (x – 5)(x² – 4). And since you're factoring completely, that becomes (x – 5)(x – 2)(x + 2).

Trying to Factor a Sum of Squares

This is a classic trap. Students get comfortable with the Difference of Squares pattern, (a² – b²), and then naturally assume a similar rule must exist for a Sum of Squares, (a² + b²).

It doesn’t.

• You can factor: x² – 16 into (x – 4)(x + 4).
• You cannot factor: x² + 16. This expression is considered prime over the real numbers.

Just remembering that a Sum of Squares is irreducible will save you a ton of time trying to make a pattern work where one doesn't exist. This drive to simplify expressions isn't new; mathematicians have been using tools and tables for centuries to make calculations easier. You can actually learn more about the historical development of factoring tools at Purdue University.

Common Questions I Hear About Factoring

As you work through more factoring problems, you'll inevitably run into the same little hurdles that trip up most students. These are the kinds of questions that come up time and time again. Let's tackle them head-on so you can factor with more confidence.

Getting these details right is what separates guessing from truly understanding the math.

What Does It Mean for a Polynomial to Be Prime?

Think of a prime polynomial just like you'd think of a prime number, like 7 or 13. A polynomial is considered prime (or irreducible) if it can't be broken down into simpler factors with integer coefficients. Its only factors are 1 and itself.

A perfect example of this is the Sum of Squares. You’ll see expressions like x² + 9 a lot. It’s tempting to try and factor it like its cousin, the Difference of Squares (x² – 9), which breaks down nicely into (x – 3)(x + 3). But the sum version just won't factor. It's prime.

But don't forget the golden rule! Always check for a Greatest Common Factor first. Something like 2x² + 18 might look prime at first glance, but you can pull a 2 out of both terms. That leaves you with 2(x² + 9). In this case, the (x² + 9) part is the prime factor.

How Do I Know Which Factoring Method to Use First?

This is probably the most important question of all, and the answer is your road map for every problem. You need a consistent strategy, a go-to order of operations for factoring.

Here’s the rule I tell all my students: Always, always, always start by looking for the Greatest Common Factor (GCF). I can't stress this enough. Pulling out the GCF first simplifies everything that follows and often makes the next step obvious.

After you've handled the GCF, let the number of terms in the polynomial guide you:

• Four Terms? Your first instinct should be factoring by grouping.
• Three Terms (a Trinomial)? This is your cue to use the standard methods you know, like trial-and-error or the AC method.
• Two Terms (a Binomial)? Immediately start hunting for special patterns: Difference of Squares, Sum of Cubes, or Difference of Cubes.

This sequence turns factoring from a chaotic guessing game into a methodical process. Developing these kinds of systematic habits is a huge part of learning math, which is something we explore more in our guide on how to study math effectively.

Does the Order of Terms Matter When I Factor by Grouping?

Sometimes, yes, but here's the good news: the method is surprisingly flexible. There's often more than one way to group the terms successfully.

Let's say you have an expression like ax + by + ay + bx. You could try grouping the first two terms together and the last two terms together. Or, you could just as easily rearrange it to ax + ay + bx + by and group those pairs.

The real test is what happens after you factor the GCF out of each pair. If you're left with a common binomial factor in the parentheses, you know your grouping worked. If it doesn't work on the first try, don't panic! Just swap the two middle terms and try again. That simple shuffle is usually all it takes to find a combination that works.

---

Struggling to get through a tough assignment or just need a second opinion on your work? Feen AI is an AI-powered homework helper that gives you clear, step-by-step explanations for Math, Physics, Chemistry, and more. Upload a picture of your problem and get the help you need to move forward with confidence. Get started at https://feen.ai.