How to Solve Quadratic Equations A Practical Guide

When you're faced with a quadratic equation—anything in that classic ax²+bx+c=0 format—your goal is to find the values of 'x' that make the equation true. The three workhorse methods you'll lean on are factoring, using the quadratic formula, and completing the square.

Each one is a different tool in your algebraic toolkit. Knowing which one to grab for a specific problem is what separates struggling from succeeding.

What Are Quadratic Equations And Why Do They Matter?

Simply put, a quadratic equation is a polynomial where the highest power of the variable is 2. That "x²" term is what makes it "quadratic" (from the Latin word for square), and it's what gives the graph its signature parabolic curve.

These U-shaped curves show up everywhere in the real world. Think about the arc a basketball makes on its way to the hoop or the flight path of a cannonball. Quadratic equations are the language we use to model these situations precisely. So, this isn't just a random algebra exercise; it's a skill with real applications in physics, engineering, and even finance.

Your Roadmap To Success

We’re going to walk through every common method, step-by-step. I'm not just going to throw formulas at you; I want you to understand why they work so you can tackle any problem with confidence.

Here’s what we’ll cover:

• Factoring: Your go-to for simpler equations that can be broken down into neat binomials. It's fast and clean when it works.
• The Quadratic Formula: The universal problem-solver. It works for any quadratic equation, even the messy ones.
• Completing the Square: A powerful technique that not only solves the equation but also helps you understand the geometry of the parabola.
• Graphing: A great visual approach for estimating solutions by seeing where the curve hits the x-axis.

Solving these equations is hardly a new idea. Archaeologists have found Babylonian clay tablets from around 2000 BCE showing geometric methods for solving quadratic-like problems to figure out land areas for taxes. They were getting answers accurate to six decimal places! It just goes to show that practical needs have always pushed mathematics forward.

The beauty of learning multiple methods is that you develop algebraic flexibility. You learn to recognize patterns and choose the most efficient tool for the job, a skill that extends far beyond your math homework.

The table below gives you a quick snapshot of the primary methods and when to use them.

Quick Guide To Solving Quadratic Equations

Method	Best For	Key Takeaway
Factoring	Simple equations where 'a' and 'c' have few factors.	Fastest method when applicable, but not always possible.
Quadratic Formula	Any quadratic equation, especially with messy numbers.	A reliable, catch-all formula that always works.
Completing the Square	When you need to find the vertex of the parabola or convert to vertex form.	More steps involved, but provides deeper geometric insight.
Graphing	Estimating solutions or when a visual representation is helpful.	Good for approximations but not for finding precise, non-integer roots.

Each technique has its place, and a true master knows when to pick each one.

Ultimately, getting comfortable with these methods builds a rock-solid foundation for more advanced math. For anyone looking to teach this material, quadratics are a cornerstone of any Algebra 2 Tutor Playbook.

Alright, let's get started.

Using Factoring for Quick and Clean Solutions

When you're faced with a quadratic equation, your first instinct should always be to see if you can factor it. It's hands-down the fastest and most direct path to the answer, but there's a catch: the equation has to be "factorable." It's like a little puzzle where you're trying to break a complex expression into its simpler, multiplied parts.

The magic behind this method is a principle called the Zero Product Property. It sounds fancy, but the idea is incredibly straightforward: if two numbers multiply to zero, one of them has to be zero. This simple rule is what makes factoring such a powerful tool for solving equations.

Simple Trinomials When 'a' Is 1

Let's start with the most common type of quadratic you'll see, where the x² term has a coefficient of 1. Your goal here is to find two numbers that check two specific boxes.

• They have to multiply to equal the constant term, 'c'.
• They also have to add up to the middle coefficient, 'b'.

Let's walk through an example: x² + 5x + 6 = 0.

In this equation, our b is 5 and our c is 6. We're hunting for two numbers that multiply to 6 and add to 5. The factor pairs of 6 are (1, 6) and (2, 3). A quick check shows that 2 + 3 = 5. Bingo. We found them.

Now, we just rewrite the equation using these two numbers: (x + 2)(x + 3) = 0

This is where the Zero Product Property kicks in. For that equation to hold true, either the (x + 2) part must be zero, or the (x + 3) part must be zero.

• If x + 2 = 0, then x = -2.
• If x + 3 = 0, then x = -3.

And there you have it—our two solutions. It’s quick, clean, and honestly, pretty satisfying to solve one this way.

Tackling Complex Cases When 'a' Is Not 1

Things get a bit more involved when the leading coefficient, 'a', is a number other than 1. This usually requires an extra step or two, often using a method called factoring by grouping. It takes a little more practice, but the core idea is the same. For a deeper look at this, our guide on how to factor polynomials completely covers these more advanced techniques in detail.

Let's try one: 2x² - 5x - 3 = 0.

First, multiply 'a' and 'c': 2 * -3 = -6. Now, the game is to find two numbers that multiply to -6 and add up to our 'b' term, which is -5. The factors of -6 are (1, -6), (-1, 6), (2, -3), and (-2, 3). The pair 1 and -6 adds up perfectly to -5.

Next, we "split" the middle term, -5x, using the two numbers we just found: 2x² + 1x - 6x - 3 = 0

Now, we group the terms into pairs and pull out the greatest common factor from each one.

• From the first pair, 2x² + x, we can factor out an x, which leaves us with x(2x + 1).
• From the second pair, -6x - 3, we can factor out a -3, leaving -3(2x + 1).

See how the expression inside both sets of parentheses is identical? That's the sign you're on the right track.

Pro Tip: When you're factoring by grouping, if the expressions inside the parentheses don't match, go back and check your work. It's almost always a simple sign error or the wrong pair of factors.

Our equation now looks like this: x(2x + 1) - 3(2x + 1) = 0

We can now factor out that common binomial, (2x + 1): (x - 3)(2x + 1) = 0

Finally, we apply the Zero Product Property one last time:

• If x - 3 = 0, then x = 3.
• If 2x + 1 = 0, then 2x = -1, which means x = -1/2.

Getting comfortable with factoring is a huge advantage. When an equation is factorable, no other method is faster. The trick is practicing enough to spot the patterns quickly, so you know when to use it and when to switch to another tool like the quadratic formula.

Mastering the Quadratic Formula for Any Equation

Sometimes, factoring just won't cut it. You'll run into quadratic equations with stubborn numbers that don't break down into neat, clean integers. When that happens, you need a tool that works every single time, no matter how messy the numbers get.

That tool is the quadratic formula—your universal key to unlocking any quadratic equation.

The formula itself can look a bit intimidating at first glance: x = [-b ± sqrt(b² - 4ac)] / 2a

But don't let its appearance fool you. Think of it as a foolproof recipe. As long as you correctly identify your ingredients—the a, b, and c values from your equation—and follow the order of operations, it will give you the right answer. This method is the direct descendant of centuries of mathematical refinement, starting with Persian scholar al-Khwārizmī in 820 CE (whose work gave us the word "algebra") and later finalized by Simon Stevin in 1594. You can discover more insights about the history of equations and their evolution over time.

Breaking Down the Formula Step by Step

Let’s walk through an equation that’s a nightmare to factor: 3x² - 4x - 5 = 0.

The first, and most crucial, step is to correctly identify your coefficients. This is where tiny mistakes can creep in, so I always recommend writing them down before you start.

• a = 3 (the coefficient of x²)
• b = -4 (the coefficient of x—don't forget that negative sign!)
• c = -5 (the constant term)

Now, we'll carefully substitute these values into the formula. Here's a pro tip: use parentheses for your substitutions, especially with negative numbers. It’s a small habit that keeps the signs straight and prevents common errors.

x = [-(-4) ± sqrt((-4)² - 4(3)(-5))] / 2(3)

This little trick saves a lot of headaches, particularly when squaring a negative number like -4. Remember, (-4)² is a positive 16, not -16.

Next, we simplify the expression piece by piece, sticking to the order of operations.

1. Simplify inside the square root: 16 - (-60) becomes 16 + 60, which equals 76.
2. Simplify the other parts: -(-4) becomes a clean 4, and 2(3) becomes 6.

Suddenly, our equation looks much more manageable: x = [4 ± sqrt(76)] / 6

The last step is to simplify the radical if we can. The number 76 can be factored into 4 * 19, so the square root of 76 simplifies to 2 * sqrt(19). This gives us our final, exact answers.

x = [4 ± 2 * sqrt(19)] / 6

Because the 4, 2, and 6 are all divisible by 2, we can simplify the entire fraction. This leaves us with our two distinct solutions: x = [2 ± sqrt(19)] / 3

The Discriminant: A Crystal Ball for Your Solutions

That expression tucked inside the square root, b² - 4ac, has a special name: the discriminant. This little piece of the formula is incredibly powerful because it tells you the nature of the solutions before you do all the work.

The discriminant is your sneak peek into the final answer. It quickly reveals whether your parabola will cross the x-axis twice, touch it once, or miss it entirely.

Here's what it tells you at a glance:

Discriminant Value	What It Means	Type of Solutions
Positive (> 0)	The parabola intersects the x-axis at two distinct points.	Two unique real solutions.
Zero (= 0)	The parabola's vertex sits exactly on the x-axis.	One real solution (a repeated root).
Negative (< 0)	The parabola never touches or crosses the x-axis.	Two complex solutions (involving i).

In our example, the discriminant was 76 (a positive number), which correctly predicted we would find two unique real solutions. If you're ever in a rush on an exam, calculating the discriminant first can be a huge time-saver. It confirms you're on the right path and tells you exactly what kind of answers to expect.

Completing the Square and Seeing the Solutions

While factoring is a great shortcut and the quadratic formula is the ultimate safety net, there's another method that offers a completely different perspective: completing the square.

At first glance, it can seem a bit roundabout. But it's actually the very technique that gives us the quadratic formula, and it’s a powerhouse for understanding the geometry hiding inside the algebra. This method is all about reshaping a standard quadratic into a perfect square trinomial—an expression that factors neatly into a squared term, like (x + k)².

The Logic Behind It

Let’s get our hands dirty with an example to see how this works: x² + 6x - 7 = 0.

First, we need to clear some space. We'll move the constant term over to the other side to isolate the terms with x. This sets the stage for building our perfect square.

x² + 6x = 7

Now for the magic. We take the coefficient of the middle term (the 6 from 6x), cut it in half, and then square that result.

1. Take the middle coefficient: 6
2. Divide by two: 6 / 2 = 3
3. Square it: 3² = 9

This number, 9, is exactly what we need to "complete" the square. To keep our equation balanced, we have to add it to both sides.

x² + 6x + 9 = 7 + 9

Look at the left side now. It’s a perfect square trinomial that simplifies beautifully to (x + 3)². The right side is just 16.

(x + 3)² = 16

We're in the home stretch. To solve for x, we just take the square root of both sides. The crucial thing here is to remember you'll get both a positive and a negative root.

x + 3 = ±4

This breaks down into two simple little equations:

• x + 3 = 4 --> x = 1
• x + 3 = -4 --> x = -7

Completing the square is more than a formula to memorize; it's a bridge connecting algebra to geometry. It's the exact process used to turn a quadratic from standard form into vertex form, a(x - h)² + k = 0, which instantly tells you the parabola's turning point.

Visualizing Solutions Through Graphing

Sometimes, the best way to understand an equation is to just look at it. Every quadratic equation, ax² + bx + c = 0, can be represented by a function, y = ax² + bx + c, whose graph is a U-shaped curve we call a parabola.

The solutions (or roots) we've been working so hard to find are simply the x-intercepts. They're the points where the parabola physically crosses the horizontal x-axis. Graphing is a fantastic way to check your work or get a gut feel for the answer.

Sketching a Quick Parabola

You don’t need graphing paper or a design degree to get a useful sketch. All you need are a few key signposts to guide you.

• Direction: Check the 'a' term. If it's positive, the parabola opens upwards (like a smile). If 'a' is negative, it opens downwards (like a frown).
• Vertex: This is the absolute bottom or top of the curve. You can find its x-coordinate with a quick calculation: x = -b / 2a. Plug that x-value back into the equation to find the matching y-value.
• Y-intercept: This one's a freebie. It’s the point where the curve crosses the vertical y-axis. Just set x = 0, and you'll find it's always the constant term, 'c'.

With just these few points, you can draw a rough parabola and see where it seems to be heading. If we were to graph y = x² + 6x - 7, our sketch would show the curve hitting the x-axis right at -7 and 1, confirming the answers we found earlier.

This visual approach is also incredibly helpful for grasping concepts like the domain and range of a function. The vertex, for example, defines the absolute minimum or maximum value in the function's range. If you want to go deeper on that, you can learn more about how to find domain and range in our detailed guide.

While graphing gives you an excellent big-picture view, it does have its limitations. If the roots are messy fractions or irrational numbers, a hand-drawn sketch will only ever be an approximation. For exact answers, you'll always want to fall back on a precise algebraic method.

Choosing The Right Method For Any Problem

So, you've got a whole toolbox of methods for tackling quadratic equations. That’s great. But the real skill—the thing that separates the pros from the novices—is knowing which tool to pull out for which job.

When a quadratic equation pops up, your first instinct shouldn't be to just start crunching numbers. It’s about taking a moment to analyze the problem and pick the smartest strategy. This isn't just about memorizing rules; it's about developing a strategic mindset to save time and avoid a lot of unnecessary work. You can develop problem-solving skills like this through deliberate practice.

This kind of strategic thinking has deep roots. Way back around 300 BCE, Euclid's Elements was laying out geometric solutions for quadratics, a system that shaped mathematics for over two thousand years. Today, that same logic helps us model everything from projectile motion—which shows up in about 60% of high school physics problems—to optimizing profits in nearly 70% of introductory business models.

Your Mental Flowchart For Solving Quadratics

Think of your approach like a quick decision tree. Before you dive in, give yourself five seconds to ask a few key questions. This mental checklist will almost always point you down the most efficient path.

To help you picture this, check out this decision tree. It's designed to walk you through the thought process for solving any quadratic equation you encounter.

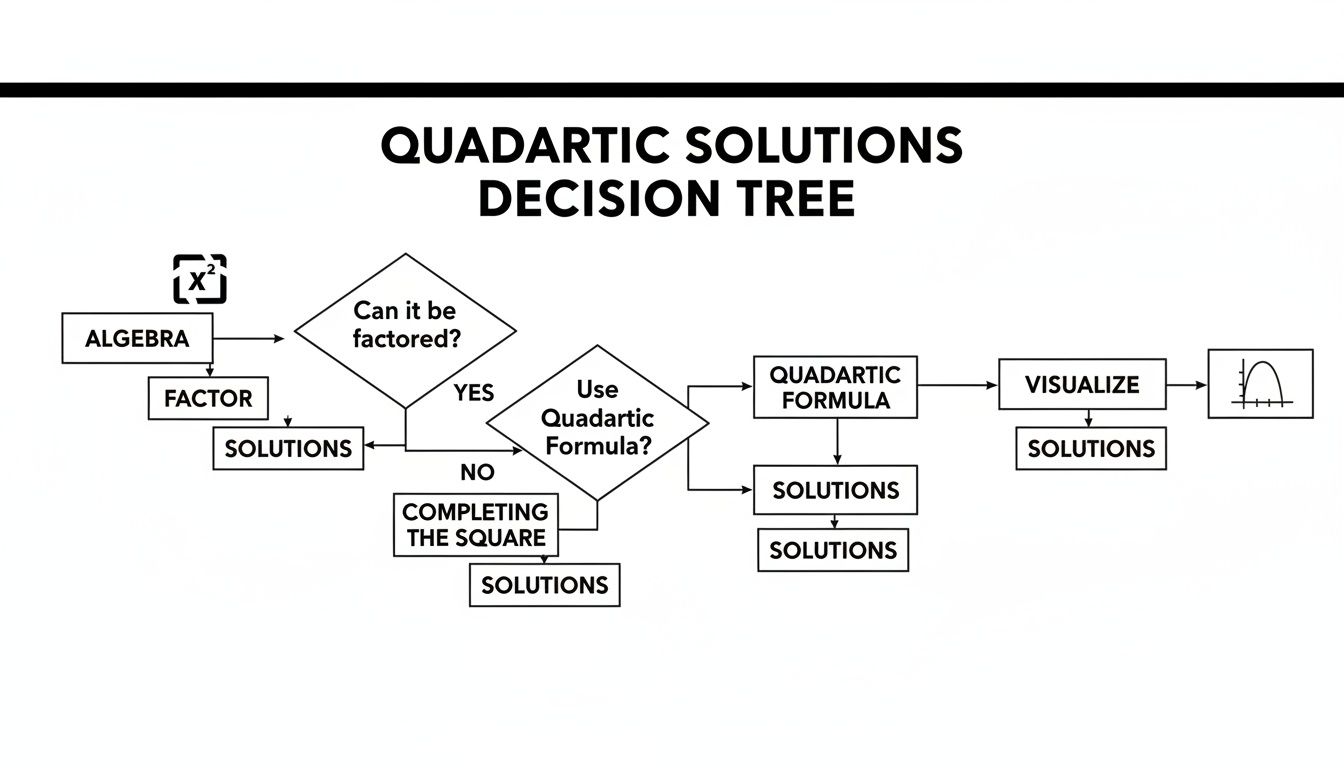
The whole idea behind this flowchart is to start with the simplest checks first before resorting to the more heavy-duty (but always reliable) methods. This ensures you’re always taking the path of least resistance.

A Practical Guide to Picking Your Method

So, how do you put that logic into practice? It really comes down to a few quick checks.

• Is the 'c' term missing? If your equation looks something like ax² + bx = 0, you've hit the jackpot. Don't even think about other methods. Just factor out an x to get x(ax + b) = 0. The solutions are always x = 0 and x = -b/a. This is the fastest win you'll ever get.

• Can I factor it in under a minute? Give the 'a' and 'c' terms a quick look. If they have just a few factors, like in x² + 5x + 6 = 0, it’s worth trying to factor it. If you spot the combination right away, perfect. But if you're still scratching your head after 60 seconds, it's time to move on. Don't waste time on a stubborn problem.

• Is it time for the quadratic formula? If you see messy coefficients, decimals, or if factoring is clearly not working, pivot straight to the quadratic formula. Think of it as your all-purpose, heavy-duty tool that works on everything. The only catch? You have to be super careful with your signs and calculations.

Pro Tip: If an exam question only asks for the number of real solutions and not the solutions themselves, go straight to the discriminant (b² - 4ac). A quick calculation there tells you if you're looking for two, one, or zero real roots, and you can save yourself a ton of time.

Which Method Should I Use? A Decision Guide

To make it even clearer, I've put together a little guide. Think of this table as your go-to reference when you're staring down a quadratic and wondering where to begin.

Situation	Recommended Method	Reasoning
The equation is ax² + bx = 0 (no constant 'c' term).	Factoring	The fastest and most direct method. Factoring out 'x' is incredibly simple.
The equation is ax² - c = 0 (no 'bx' term).	Square Root Method	Isolating x² and taking the square root is much quicker than other methods.
'a', 'b', and 'c' are simple integers and factoring seems likely.	Factoring	If you can spot the factors quickly (under a minute), it's the most elegant solution.
The numbers are large, have decimals, or factoring isn't working.	Quadratic Formula	Your universal tool. It's guaranteed to work for any quadratic equation, every time.
You need to find the vertex (max/min point) of the parabola.	Completing the Square	This method directly converts the equation into vertex form, y = a(x - h)² + k.
You only need to know how many real solutions exist.	The Discriminant	b² - 4ac quickly tells you if there are 2, 1, or 0 real solutions without solving.
You need a visual representation or the roots are difficult to find.	Graphing	Useful for visualizing the parabola and approximating the solutions (x-intercepts).

This isn't about rigid rules, but about building intuition. With a little practice, you'll start to recognize the best approach just by looking at the equation.

How Real-World Problems Shape Your Choice

The context of a problem can also give you a major hint about which method to use. Real-world applications often show up as word problems, which add a translation step to the process. For help with those, our guide on https://feen.ai/blog/how-to-solve-word-problems-in-algebra has some great practical strategies.

Here’s how the scenario can point you in the right direction:

• Physics and Projectile Motion: When a problem asks, "when does the rocket hit the ground?" you'll often end up with an equation that has non-integer solutions. The quadratic formula is your best friend here, giving you the precise answer you need.

• Geometry and Area: If you're calculating the dimensions of a rectangular garden, the resulting quadratic is often set up to be easily factorable.

• Engineering and Design: An architect designing a bridge with a parabolic arch needs to know its highest point. This is a perfect case for completing the square, as it directly finds the vertex of the parabola.

By practicing this decision-making process, you'll stop seeing quadratic equations as one big, scary task. Instead, they become a series of unique puzzles, each with its own elegant and efficient solution just waiting to be found.

Avoiding Common Mistakes for Exam Success

Knowing the formulas is one thing, but executing them flawlessly under pressure is a completely different skill. I've seen countless students understand the concepts perfectly but still lose points on exams because of small, preventable errors. Let's talk about the common traps and how to sidestep them.

The single most common mistake? Sign errors. It's so easy to do, especially when you're rushing. A classic example is substituting a negative 'b' value into the quadratic formula. People forget that the -b part means -(-b), which turns into a positive. That one tiny mistake throws the whole calculation off right from the start.

Another frequent pitfall happens during factoring. You're looking for two numbers that multiply to 'c' and add up to 'b'. It’s tempting to grab the first pair of factors you see for 'c' without checking if they also add up to 'b'. Always double-check both conditions.

Building a Bulletproof Process

Your best defense against these silly mistakes isn't being a math genius; it's about having a solid, repeatable process. A few disciplined habits can dramatically boost your accuracy.

Before you even think about solving, physically write down the values for 'a', 'b', and 'c' at the top of your paper. It takes maybe five seconds, but it forces you to consciously identify each coefficient, drastically cutting down on substitution errors.

My Favorite Pro Tip: When you get your final answer(s), plug at least one of them back into the original equation. I know it feels like extra work, but it's the only way to be 100% certain you're correct. This quick check has saved me—and my students—from countless little calculation blunders.

Smart Exam-Day Strategies

On a timed test, how you manage your minutes is just as important as how you do the math. If a quadratic is giving you trouble, don't just stare at it and waste time.

Here's a quick tactical move: calculate the discriminant (b² - 4ac) first.

• Is it a perfect square? Great, that means the equation is factorable. Give factoring one more honest shot.
• Is it a non-perfect square or negative? Stop trying to factor immediately. It's a waste of time. Go straight to the quadratic formula.

This little diagnostic check tells you the most efficient path forward, preventing you from getting stuck in a dead-end.

Finally, if the clock is ticking and you can't finish a problem, never leave it blank. At the very least, write down the correct formula and show that you've correctly substituted the 'a', 'b', and 'c' values. Many instructors will give you partial credit for showing you know the process, which is a whole lot better than getting a zero.

Frequently Asked Questions

Even after you've got the main solving methods down, some quadratic equations can still throw you a curveball. Let's walk through some of the common questions and tricky situations that pop up.

What Happens if a Term Is Missing in the Equation?

It's pretty common to find an equation that's missing a term. Don't sweat it—this actually simplifies things.

If the 'b' term is missing, like in x² - 9 = 0, the quickest route is just to isolate the x² term and take the square root. Get the constant to the other side (x² = 9) and solve from there. The crucial thing is to remember both the positive and negative roots. In this case, x = ±3.

What if the 'c' term is missing? For an equation like 2x² + 8x = 0, factoring is your best friend. There will always be a common factor of 'x'. Here, you can pull out 2x, leaving you with 2x(x + 4) = 0. The Zero Product Property then tells you the solutions are x = 0 and x = -4.

Can a Quadratic Equation Have Only One Solution?

Absolutely, and it happens more often than you might guess. Think about it graphically: this is when the parabola’s vertex (its peak or valley) rests right on the x-axis, touching it at just one spot.

Algebraically, a single solution means the discriminant (b² - 4ac) works out to be exactly zero. This is a dead giveaway that you're dealing with a perfect square trinomial. An equation like x² - 6x + 9 = 0 factors cleanly into (x - 3)² = 0, giving you that one solution: x = 3.

What Are Imaginary and Complex Solutions?

Sometimes, a parabola just doesn't cross the x-axis at all. When this is the case, the discriminant (b² - 4ac) will be negative. Since you can't take the square root of a negative number in the real number system, there are no real solutions.

This is where imaginary and complex numbers enter the picture. These answers use the imaginary unit, 'i', which is simply the square root of -1. You'll see them written in the standard form a + bi. While they won't show up as x-intercepts on a regular graph, they are incredibly important in advanced math and science, especially in fields like electrical engineering and quantum physics.

---

Staring at a problem that won’t budge or need a quick check on your homework? Feen AI can give you a hand. Snap a picture of your equation, and our AI helper will walk you through it step-by-step. It works for Math, Physics, and Chemistry questions. Get instant clarity and solve problems with confidence.