Understanding change in momentum: A Practical Guide

Let's ditch the dry, textbook definitions for a moment. You already know what a change in momentum feels like, even if you don't call it that. It's the jolt you feel when a car suddenly brakes, or the satisfying crack of a baseball reversing course after connecting with a bat. It's the physical consequence of altering an object's "mass in motion."

What Does Change in Momentum Actually Mean?

Think about catching a fast-moving baseball. That sting in your glove? It isn't just about the ball's speed. It’s the direct result of the ball's momentum going from full tilt to a dead stop in a fraction of a second. That single experience captures the essence of a change in momentum perfectly.

It’s a concept that marries an object's mass with its motion. A heavy bowling ball rolling slowly still has a ton of momentum because it has so much mass. On the flip side, a feather-light tennis ball can have significant momentum too, but only if it's moving at a very high speed.

Any time you alter an object's speed or its direction, you're causing a change in its momentum.

The Core Formula for Change in Momentum

To put a number on this feeling, we start with a really simple idea. The "change" in anything is just where it ended up minus where it started. For momentum, it looks like this:

Δp = p_final - p_initial

In this equation, Δp (we say "delta-p") stands for the change in momentum. It’s simply the final momentum (p_final) minus the initial momentum (p_initial). This gives us the total shift that happened.

But we can take this a step further to make it much more useful. We know that momentum (p) is just mass (m) multiplied by velocity (v). Assuming the object's mass doesn't change (which is almost always the case in these problems), the change in momentum boils down entirely to the change in its velocity (Δv).

This brings us to the go-to formula for actually calculating the change in momentum: Δp = mΔv, which can be expanded to Δp = m(v_final - v_initial).

This little equation tells a big story. It shows that a huge, slow-moving object can experience the same change in momentum as a tiny object that undergoes a massive change in velocity. It's the interplay between mass and the shift in motion that really counts.

Connecting Force and Time with the Impulse-Momentum Theorem

So, we know momentum can change. But why does it change? Answering that question is where the real physics gets interesting. This leads us straight to the Impulse-Momentum Theorem, a powerful idea that neatly ties together force, time, and the change in momentum.

The theorem itself is beautifully simple: the impulse acting on an object is equal to the change in that object's momentum.

First, let's nail down what impulse is. Think of it as the total "oomph" delivered to an object. It's the product of the net force acting on something and the amount of time that force is applied. The harder you push, or the longer you push for, the greater the impulse. We write this as:

J = F_net * Δt

Here, J stands for impulse, F_net is the net force, and Δt is the time interval.

Two Sides of the Same Coin

The Impulse-Momentum Theorem brings everything together by stating that this impulse (J) is exactly equal to the change in momentum (Δp). This gives us the complete relationship:

F_net * Δt = Δp

This little equation reveals something profound. Impulse and change in momentum aren't two separate things happening one after the other. They are just two different ways of looking at the very same physical event. One describes the cause (a force applied over time), while the other describes the effect (a change in the object's motion).

This concept map helps visualize how an object's mass and velocity create its momentum in the first place.

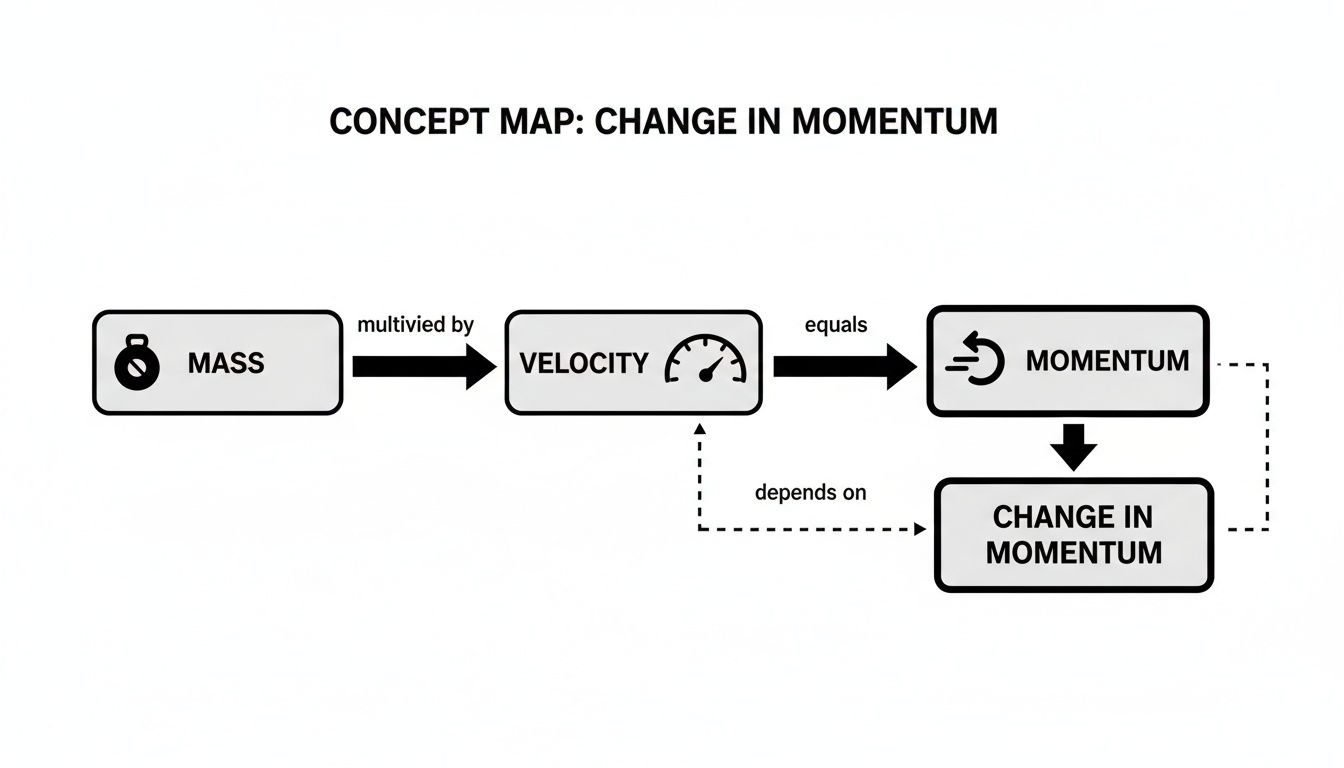
As you can see, any change in velocity directly creates a change in momentum—and the impulse-momentum theorem tells us exactly how that happens.

Practical Applications of Impulse

You can see this principle at work all around you. Take a car's airbag. During a collision, your change in momentum is a fixed value; you have to go from a high speed to zero. The airbag can't change that. What it can do, however, is brilliantly manipulate the time (Δt) over which you slow down.

By dramatically increasing the duration of the impact, the airbag drastically reduces the average force (F) exerted on your body, often making the difference between walking away and a serious injury.

This idea even applies at the most extreme scales. During the Trinity atomic test on July 16, 1945, a plutonium core of just 6.2 kilograms experienced a massive fission reaction. This unleashed an unimaginable force over a few microseconds, creating an enormous change in momentum estimated at over 10^6 kg·m/s that produced the devastating shockwave. To dig deeper into how forces and momentum are connected, you might find it helpful to look into resources for tackling common forces questions.

This theorem isn't just a standalone rule; it's a direct consequence of an even more fundamental concept in physics. You can trace its roots back by reading our guide on what Newton's Second Law is.

How to Solve Change in Momentum Problems

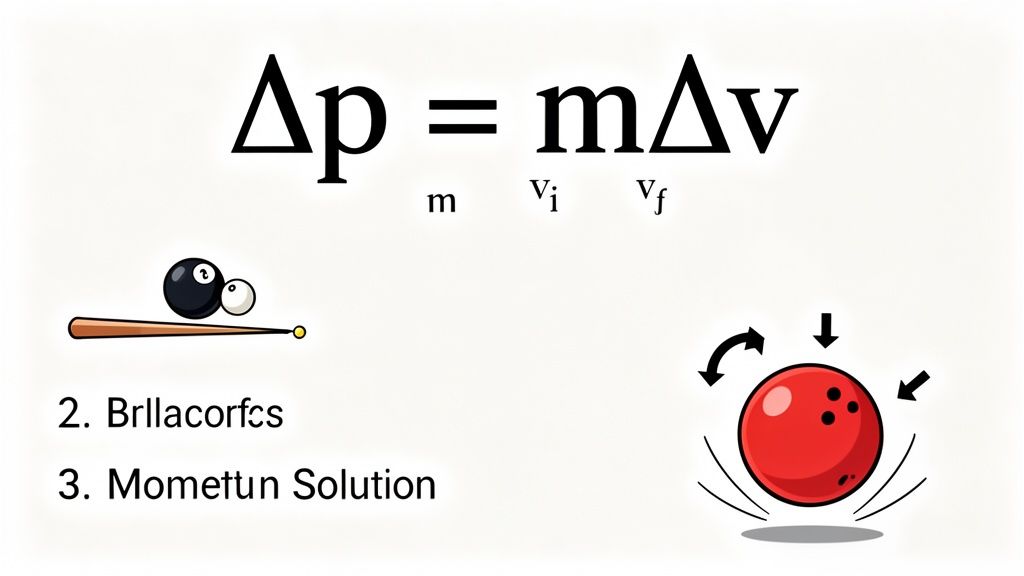
Moving from theory to actually solving problems is where the rubber meets the road. Once you get a reliable process down, calculating the change in momentum becomes second nature. The real trick is to break down the problem methodically, identify what you know, and pick the right tool—in this case, the right formula—for the job.

Most problems will hand you a few key pieces of information: mass (m), initial velocity (v_initial), final velocity (v_final), force (F), or the time interval (Δt). Your mission is to find the missing piece of the puzzle.

Having a go-to strategy is the best way to build confidence and nail the answer every time.

A Step-by-Step Approach to Solving Momentum Problems

Here’s a simple, four-step method that works for just about any momentum problem you'll encounter:

1. List Your Knowns and Unknowns: First things first, read the problem carefully. Jot down every value you're given and label it with the correct variable (e.g., m = 10 kg). Then, clearly state what you're trying to find (e.g., Δp = ?). This simple act of organization prevents a lot of headaches.

2. Assign a Positive Direction: This is a big one. Momentum is a vector, which means direction is everything. Before you do any math, decide which direction is positive (like "to the right") and which is negative. Any velocity moving in that negative direction must get a negative sign.

3. Choose the Right Formula: Now, look at the list of variables you made.

   • If you have mass and velocities, your best bet is Δp = m(v_final - v_initial).
   • If you have force and time, you'll want to use the impulse formula, J = FΔt, because impulse is the same thing as the change in momentum (J = Δp).

4. Solve for the Unknown: Plug your known values into the equation and do the math. Don't forget to tack on the correct units—kg·m/s—to your final answer.

This structured process takes the guesswork out of it. And if you ever need a quick refresher on the formulas, our comprehensive physics formulas cheat sheet is a great resource to keep handy.

To help you get comfortable with these calculations, here’s a quick-reference table summarizing the key equations.

Key Formulas for Momentum and Impulse

Concept	Formula	Variable Definitions	SI Units
Momentum	p = mv	p = momentum m = mass v = velocity	kg·m/s
Change in Momentum	Δp = mΔv or Δp = m(v_f - v_i)	Δp = change in momentum m = mass Δv = change in velocity v_f = final velocity v_i = initial velocity	kg·m/s
Impulse	J = FΔt	J = impulse F = net force Δt = time interval	N·s (Newton-seconds)
Impulse-Momentum Theorem	FΔt = mΔv or J = Δp	This theorem equates impulse to the change in momentum.	N·s = kg·m/s

This table is your toolkit. Now, let's see how to use these tools with a couple of real examples.

Example 1: Straight-Line Collision

Let's put the four-step method into action. A 0.5 kg billiard ball is zipping along at 4 m/s. It hits a stationary ball and comes to a dead stop. What was the change in momentum of that first ball?

• Step 1: List Knowns & Unknowns.

  • Knowns: m = 0.5 kg, v_initial = 4 m/s, v_final = 0 m/s.
  • Unknown: Δp = ?

• Step 2: Assign Direction. We'll say its initial direction of travel is positive.

• Step 3: Choose Formula. We have mass and two velocities, so Δp = m(v_final - v_initial) is the way to go.

• Step 4: Solve.
  Δp = 0.5 kg * (0 m/s - 4 m/s) = -2 kg·m/s.

That negative sign is important. It tells us the change in momentum was in the opposite direction of the ball's initial motion. This makes perfect sense, because an opposing force is what brought it to a stop.

Example 2: Reversing Direction

Okay, now for a slightly trickier one. A 0.4 kg rubber ball smacks into a wall at 10 m/s and bounces straight back at 8 m/s. What is its change in momentum?

Key Insight: This is where Step 2 saves the day. The most common mistake people make here is forgetting to assign a negative sign to the rebound velocity. If you miss that, your answer will be way off.

Let's walk through it:

• Step 1: List Knowns & Unknowns.

  • Knowns: m = 0.4 kg, v_initial = 10 m/s, v_final = -8 m/s.
  • Unknown: Δp = ?

• Step 2: Assign Direction. Let's call the direction towards the wall positive. This means the rebound velocity must be negative.

• Step 3: Choose Formula. Again, we have mass and velocities, so we'll use Δp = m(v_final - v_initial).

• Step 4: Solve.
  Δp = 0.4 kg * (-8 m/s - 10 m/s)
  Δp = 0.4 kg * (-18 m/s) = -7.2 kg·m/s.

Seeing Momentum Change in the Real World

The principles of momentum aren’t just trapped inside physics labs or textbook problems. Once you know what to look for, you'll start seeing the change in momentum everywhere. It’s the invisible hand shaping everything from clever engineering designs to the most thrilling moments in sports.

Take a rocket launch, for instance. Getting that massive machine to escape Earth's gravity is an incredible challenge. To do it, the rocket blasts enormous amounts of hot gas downwards at incredible speeds. While each gas particle has a tiny mass, their combined downward change in momentum is colossal. This generates an equal and opposite upward change in momentum for the rocket, pushing it toward the stars.

This is the impulse-momentum theorem playing out on a grand scale. The engine's continuous force (F) applied over time (Δt) produces a gigantic change in the rocket's momentum (Δp).

Impulse and Safety Engineering

Automotive safety is another field that’s all about manipulating momentum. A car’s crumple zone, for example, is a brilliant piece of engineering designed specifically to manage the impulse during a collision. When a car crashes, its momentum has to drop to zero, and it happens fast.

The crumple zone can’t reduce the total change in momentum—that’s fixed by the car's mass and speed. What it can do is buckle and deform, which dramatically increases the time (Δt) over which the impact occurs. By stretching out that duration, the average force (F) transferred to the passengers is drastically reduced. That’s what saves lives.

In essence, safety features like crumple zones and airbags are just clever applications of the equation FΔt = Δp. They make collisions survivable by intelligently stretching 't' to shrink 'F'.

Momentum in Sports

You don't have to look any further than your favorite sport to see athletes masterfully using impulse to change an object's momentum.

• Hockey Slap Shot: A player winds up and swings, putting a massive force on the puck for a split second. This huge impulse takes the puck from a standstill to over 100 mph—a truly dramatic change in momentum.
• Football Tackles: The high-stakes world of American football is built on momentum-altering collisions. When a 100 kg linebacker stops a 90 kg running back sprinting at 10 m/s in just 0.2 seconds, they're delivering an impulse of 900 kg·m/s. With an average of 250 tackles per game during the 2023 NFL season, over 68,000 of these powerful impulse events happened, each one a raw display of physics in action.

From engineering marvels to athletic triumphs, understanding this principle reveals how fundamental physics dictates the outcome of events all around us. While momentum describes an object's motion in progress, it's a close cousin to another key concept, which you can explore in our article covering examples of inertia.

Common Mistakes and Misconceptions to Avoid

When you're first getting your head around momentum, a few common tripwires can pop up. Let's clear these up right away, so you can build a rock-solid understanding from the start.

Momentum Isn't Kinetic Energy

One of the most common mix-ups is treating momentum and kinetic energy like they're the same thing. They're related, sure, because they both involve an object's motion, but they tell us different stories.

Think of it this way: momentum (p = mv) is all about "mass in motion" and it has a direction. Kinetic energy (KE = ½mv²), on the other hand, is a scalar quantity that just tells you how much energy that motion has. While an object needs kinetic energy to have momentum, the two concepts are not interchangeable.

The Biggest Pitfall: Forgetting Direction

If there's one mistake that catches everyone, it's this: forgetting that momentum is a vector. That little detail is everything. It means momentum doesn't just have a size; it has a direction, and you have to account for it.

When you're working through a problem, the first thing you should do is define your directions. For instance, "right" is positive, and "left" is negative. Forgetting this simple step is probably the number one reason for wrong answers on physics tests. If a car hits a wall and bounces backward, its final velocity has to have the opposite sign from its initial velocity.

Key Takeaway: A change in direction is a change in velocity. This means there's a significant change in momentum, even if the object’s speed stays nearly the same.

Imagine a soft foam ball and a hard rock with the exact same mass and speed hitting a wall. They both experience the same change in momentum. But the rock transfers that momentum in a fraction of a second, which is why it delivers a much larger, more damaging force.

This is what makes the physics of sports so interesting. Take a basketball rebound, for example. A 0.6 kg ball hitting the backboard at 10 m/s and bouncing off can see its momentum change by 6 kg·m/s in that split second. For students tackling these ideas, new learning tools that can visualize trajectories or break down biomechanics are becoming a game-changer in an education technology market that's projected to hit $572 billion by 2034. You can explore the growth of this market in recent industry analysis for more details.

Ready to Test Your Skills?

Watching examples and reading through the theory is one thing, but the best way to really get a handle on physics is to roll up your sleeves and solve some problems. It's in the process of working through the numbers that the concepts truly click. This is where you build the intuition to connect formulas to what’s actually happening.

Think of this section as your personal training ground for momentum and impulse. The problems start off straightforward and then gradually introduce more layers, pushing you to apply the impulse-momentum theorem in different contexts.

My Advice? Try to solve each problem on your own first, before peeking at the answers. Seriously. The real learning happens when you wrestle with the problem, even if you get stuck or make a mistake along the way.

Ready to see what you've got? Let’s do this.

Momentum and Impulse Practice Questions

Here are three classic scenarios. Grab a pencil and calculator and see if you can work out the change in momentum and the forces involved.

1. The Tennis Serve: A tennis pro smacks a 0.06 kg ball, sending it flying off the racket at 55 m/s. If the racket and ball were in contact for just 0.005 seconds, what was the average force the racket slammed into the ball with?

2. The Bouncing Ball: A rubber ball with a mass of 0.25 kg is dropped. It hits the floor moving at 10 m/s and bounces right back up at 8 m/s. What's the ball’s change in momentum? (Hint: Direction matters!)

3. The Skateboard Push: A 60 kg skateboarder is standing still. Her friend gives her a quick push that lasts 0.5 seconds, causing her to glide away at 2 m/s. Can you figure out the impulse her friend delivered and the average force of that push?

Give each one a shot using the methods we've covered. This is the best way to lock in the concepts and feel confident for your next test or homework assignment.

If you hit a wall, don't sweat it—that's part of the process. You can always ask an AI tool like Feen for a little nudge in the right direction or to double-check your logic.

After you’ve tried them all, compare your work with the detailed solutions in the next section. Getting that instant feedback is key to catching any small mistakes and reinforcing the right way to tackle these problems.

Common Questions About Change in Momentum

Even after you've got the formulas down, a few tricky concepts can still trip you up. Let's clear up some of the most common questions about how momentum works in the real world.

Is Impulse the Same Thing as a Change in Momentum?

Not quite, but they are two sides of the same coin. The simplest way to think about it is that impulse is the cause and the change in momentum is the effect.

• Impulse (J = FΔt) is the force that acts on an object over a certain amount of time. It's the "push" or the "impact."
• Change in Momentum (Δp) is the direct result of that impulse. It’s how much the object's motion actually changes.

The Impulse-Momentum Theorem connects them, showing that J = Δp. So, while they describe different aspects of an interaction, their numerical values are always equal.

Why Does Momentum Have a Direction?

Momentum is a vector because it’s built from velocity, which is also a vector. Vectors are quantities that have both a size (magnitude) and a direction. Forgetting to account for direction is probably the single most common mistake people make when solving momentum problems.

Think about it: a bowling ball heading east is doing something very different from an identical ball heading west at the same speed.

A change in direction is a change in velocity, and that means a change in momentum has definitely occurred.

This is why a tennis ball bouncing off a racket experiences a huge change in momentum—its velocity flips from positive to negative, which is a massive shift.

What's the Difference Between Elastic and Inelastic Collisions?

The main difference is all about kinetic energy. In any collision—elastic or inelastic—the total momentum of the system is always conserved. Kinetic energy, however, is a different story.

• In a perfectly elastic collision, kinetic energy is also conserved. It's a "clean" collision. Picture two billiard balls clicking off each other perfectly, with no energy wasted as sound or heat.

• In an inelastic collision, some of the kinetic energy gets converted into other forms, like sound, heat, or the energy needed to permanently bend or break something. A car crash is the classic example; a huge amount of kinetic energy is spent crumpling the metal frames.

---

Struggling with a tricky physics problem or need a concept explained differently? Feen AI can help. Upload a photo of your assignment or just ask a question to get step-by-step solutions and clear explanations for Physics, Chemistry, Math, and more. Get unstuck and master your coursework by visiting https://feen.ai.