A Chemist's Guide to Converting Mass to Moles

Welcome to what is arguably the most fundamental skill in all of chemistry: converting mass to moles. This calculation is the essential bridge connecting what you can actually weigh on a scale in the lab to the invisible world of atoms and molecules.

Let's get straight to it. To convert the mass of a substance into moles, you just need to divide its mass by its molar mass. The formula looks like this: n = m / M. That's the core of it all.

Why This One Calculation Is So Incredibly Important

Getting a handle on the mass-to-moles conversion is about more than just acing a quiz; it’s about learning to speak the language of chemistry. This single calculation allows us to make sense of the microscopic world in tangible, measurable ways. It's the absolute bedrock of stoichiometry—the part of chemistry that deals with the amounts of stuff involved in reactions.

Without this conversion, predicting how a chemical reaction will turn out would be pure guesswork.

Think about it like a recipe. You might need two eggs and a cup of flour. Counting eggs is easy, but you have to weigh the flour. In chemistry, we can't possibly count individual atoms, so we "weigh" them in big, standardized groups called moles. This is the calculation that lets chemists answer the most critical questions:

• How much product can I realistically expect to make?
• Which of my starting materials is going to run out first?
• What's the actual concentration of this solution I just made?
• How can I run this reaction to be as efficient as possible, with minimal waste?

The Mass to Moles Conversion Formula at a Glance

Before we dive deeper, let's break down the formula into its parts. This simple table gives you a quick reference for each component you'll be working with.

Variable	Symbol	Description	Unit
Moles	n	The amount of substance, representing a specific number of particles (6.022 x 10²³).	mol
Mass	m	The quantity of the substance measured on a scale.	grams (g)
Molar Mass	M	The mass of one mole of a substance, found using the periodic table.	grams per mole (g/mol)

Think of this table as your cheat sheet. Every time you see a problem asking you to jump between the mass of a substance and the amount of it, this formula is your starting point.

From a Clever Idea to a Global Standard

Being able to connect a substance's weight to a specific number of particles wasn't always so simple. The concept traces its roots way back to the early 19th century. In 1811, Amedeo Avogadro first suggested that equal volumes of gases under the same conditions contain the same number of molecules. This was a massive leap forward, laying the groundwork for linking mass to a particle count.

The idea was refined over the next century and a half until 1971, when the mole was officially adopted as one of the seven base units in the International System of Units (SI). This move standardized these crucial conversions for scientists everywhere.

At its heart, converting mass to moles is about translating a measurement you can see and feel (grams) into a quantity that makes sense on the atomic scale (moles). This shift in perspective is what makes precise, predictable, and safe chemistry possible in labs and industries all over the world.

Learning this conversion is your ticket to nearly every quantitative problem you'll face in chemistry. It unlocks calculations for chemical reactions, solution concentrations, gas laws, and so much more. This isn't just about passing the next test; it's about truly understanding how we measure the building blocks of matter itself.

Calculating Molar Mass with Confidence

Before you can even think about converting mass to moles, you need one crucial piece of the puzzle: the molar mass. Think of it as the specific "weight" of one mole of any substance, always measured in grams per mole (g/mol).

Getting this number right is everything. A tiny mistake here throws your entire calculation off, no matter how perfectly you handle the final division.

Your go-to tool for this is the periodic table. It gives you the atomic mass for every element—the average mass of a single atom. For our purposes, we just take that number and stick g/mol on the end to represent the element's molar mass.

This flowchart breaks down how central the molar mass is to the whole process.

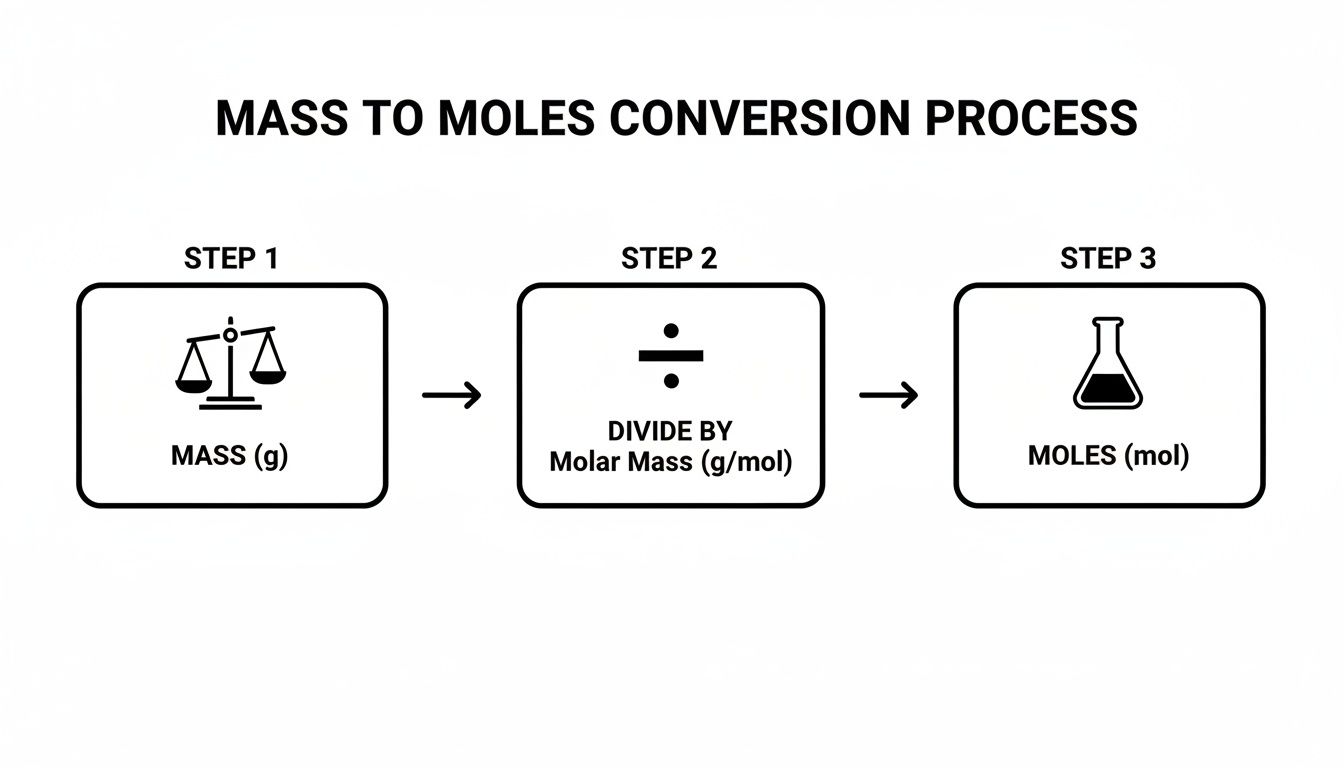
As you can see, the entire conversion really pivots on finding the correct molar mass to use as your conversion factor.

Finding Molar Mass for Elements and Compounds

Let's start with the basics. For a single element like aluminum (Al), you just look it up on the periodic table. Simple. The molar mass of aluminum is 26.98 g/mol.

Now for molecules. Take diatomic oxygen (O₂), the oxygen we breathe. You find oxygen's atomic mass (which is about 16.00 g/mol) and just multiply it by that little subscript, 2.

• Molar Mass of O₂ = 2 × (Molar Mass of O) = 2 × 16.00 g/mol = 32.00 g/mol

This same logic scales up to more complex compounds. You're just adding up the molar masses of all the individual atoms in the chemical formula. In professional settings, sourcing reliable data like this is vital, which is why understanding things like Safety Data Sheet compliance is so important.

Tackling Complex Chemical Formulas

What happens when you run into something with parentheses, like calcium phosphate, Ca₃(PO₄)₂? It looks a bit intimidating, but the rule is simple: treat the subscript outside the parentheses as a multiplier for everything inside.

Let's break it down piece by piece:

• Calcium (Ca): The subscript is 3, so we have 3 atoms. (3 × 40.08 g/mol) = 120.24 g/mol
• Phosphorus (P): There's 1 atom inside the parentheses, which gets multiplied by the 2 outside. (1 × 2 × 30.97 g/mol) = 61.94 g/mol
• Oxygen (O): We have 4 atoms inside, which also gets multiplied by the 2 outside. (4 × 2 × 16.00 g/mol) = 128.00 g/mol

Now, just add them all together: 120.24 + 61.94 + 128.00 = 310.18 g/mol. That’s the molar mass for Ca₃(PO₄)₂. Once you have this number, you're all set for the final conversion step.

If you want a more detailed walkthrough with extra practice, our complete guide on how to calculate molar mass is the perfect next step: https://feen.ai/blog/how-to-calculate-molar-mass.

Putting the Formula to Work: Real-World Examples

Alright, you've got the theory down and you know how to calculate molar mass. Now let's get our hands dirty and see how this works in practice. This is where the concept clicks—when you take a real, tangible mass and figure out exactly how many moles of a substance you're holding.

We'll start simple and then move on to compounds you'd find in any lab setting. The great thing is, the core process never changes. You'll always come back to that one trusty formula: n = m / M.

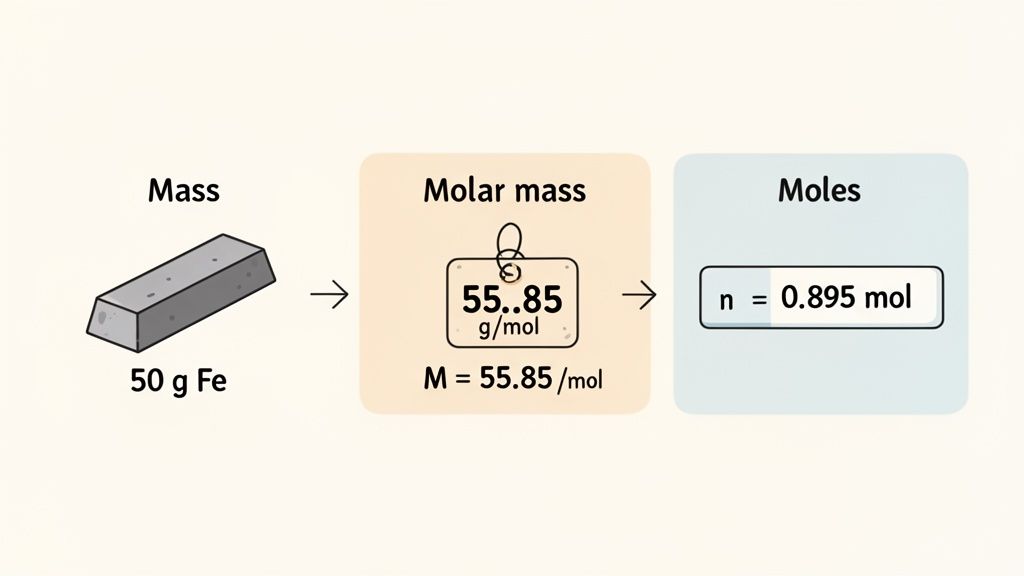
Example 1: An Iron Bar

Picture this: you have a small iron bar sitting on a scale, and it reads exactly 50.0 grams. How many moles of iron atoms are packed into that bar? This is a perfect, straightforward starting point.

First, let's list what we know:

• The mass (m) is 50.0 g.
• The substance is pure iron (Fe).

Now, we just need the molar mass (M) of iron. A quick look at the periodic table tells us it's about 55.85 g/mol. With both pieces of the puzzle, we can solve it.

Moles (n) = Mass (m) / Molar Mass (M)

n = 50.0 g / 55.85 g/mol

n ≈ 0.895 moles of Fe

See how the "g" units cancel out, leaving you with moles? It's a handy little sanity check to make sure your setup is correct. So, that 50-gram iron bar contains just under a mole of iron atoms.

Example 2: A Beaker of Water

Let's move on to a compound. Imagine you're in the lab and you've carefully measured out 100.0 grams of pure water (H₂O) for an experiment. How many moles of water molecules are in that beaker?

The first step is the same: our mass is 100.0 g. But this time, we have to quickly calculate the molar mass for H₂O ourselves.

• Hydrogen (H): We have 2 atoms, so 2 × 1.01 g/mol = 2.02 g/mol
• Oxygen (O): We have 1 atom, so 1 × 16.00 g/mol = 16.00 g/mol
• Total Molar Mass (M): 2.02 + 16.00 = 18.02 g/mol

Now that we have our molar mass, the final calculation is just a simple division.

Moles (n) = 100.0 g / 18.02 g/mol

n ≈ 5.549 moles of H₂O

That 100.0-gram sample contains about five and a half moles of water. This is the kind of calculation chemists do all the time, especially when they need to prepare solutions with a very specific concentration.

Example 3: Table Salt on a Scale

Let's try one more common substance: sodium chloride (NaCl), otherwise known as table salt. You weigh out a small pile that comes to 25.0 grams. How many moles is that?

You know the drill. We start by finding the molar mass of NaCl.

• Sodium (Na): 1 × 22.99 g/mol = 22.99 g/mol
• Chlorine (Cl): 1 × 35.45 g/mol = 35.45 g/mol
• Total Molar Mass (M): 22.99 + 35.45 = 58.44 g/mol

With that number in hand, we can do the final conversion.

Moles (n) = 25.0 g / 58.44 g/mol

n ≈ 0.428 moles of NaCl

These examples really drive home how a single, reliable process works for any substance. It doesn't matter if it's a pure element or a complex molecule. The key is to be methodical: identify your mass, find or calculate the molar mass, and then divide.

Once you're comfortable with these basic conversions, you'll be well-prepared for more advanced problems. If you're ready to test your skills on more complex scenarios, working through a set of stoichiometry practice problems with answers is a fantastic next step to build both your speed and your confidence.

How Mole Conversions Shape Our World

It's easy to dismiss converting mass to moles as just another abstract exercise from a high school chemistry class. But the truth is, this single skill is one of the most practical and powerful tools in the scientist's toolkit, underpinning critical work in countless professional fields.

When you get a handle on this conversion, you're essentially learning to speak the language of chemists, engineers, and researchers who are quite literally building the world around us. This is where the numbers on the page jump into the real world.

Think about pharmaceuticals, where a tiny mistake can have huge consequences. A scientist developing a new drug doesn't just scoop a random amount of a compound into a beaker. They have to know exactly how many molecules they're working with, and that means converting a measured mass into a precise number of moles. It’s the key to making sure a dose is effective but, more importantly, safe.

A World Built on Moles

Once you start looking, you'll see the impact of this calculation everywhere.

Take the smartphone in your pocket or the airplane flying overhead. The advanced alloys that make them both strong and lightweight are developed by materials scientists who live and breathe mole conversions. By controlling the exact molar ratios of elements like aluminum, titanium, or nickel, they can dial in the final material's properties with incredible precision.

It’s the same story in environmental science. When an environmental chemist pulls a water sample from a river, they measure pollutants in grams or milligrams. But to understand the true toxicity and concentration, they must convert that mass into moles. That calculation tells them if the water is safe or if they need to raise an alarm.

Even the food on your table gets there thanks to this conversion. Fertilizer production is a massive chemical process where manufacturers need to combine reactants in perfect molar ratios to get the highest possible yield without wasting expensive materials.

The real-world stakes are enormous. Mishandling mass-to-mole conversions can lead to huge inefficiencies and even danger. The pharmaceutical industry, for example, is estimated to lose around $50 billion each year from manufacturing errors, many of which stem from basic stoichiometry mistakes. You can dig deeper into why these conversions are so critical on Study.com.

From the Lab Bench to the Real World

See how different professional fields apply mass-to-mole conversions in their daily work.

Mass to Moles in Action Across Industries

Industry	Practical Application	Example Substance
Pharmaceuticals	Ensuring correct dosage of active ingredients in medication.	Acetaminophen (C₈H₉NO₂)
Agriculture	Optimizing reactant ratios for fertilizer production.	Ammonia (NH₃)
Materials Science	Forging metal alloys with specific properties.	Stainless Steel (Fe, Cr, Ni)
Environmental Safety	Measuring pollutant concentrations in water and air.	Lead (Pb)

This isn't an exhaustive list, but it gives you a sense of just how fundamental this skill is. Whether it’s a food scientist perfecting the flavor profile of a new energy drink or a forensic expert analyzing trace evidence, the ability to think in moles is what separates theory from practice.

Learning this conversion doesn't just help you pass a test; it connects you to the work that drives modern science and industry. It’s a skill that empowers you to quantify and manipulate the world at a molecular level.

Where People Get Tripped Up (And How You Can Avoid It)

Even a calculation as fundamental as converting mass to moles has its share of tripwires. I've seen these same mistakes trip up students year after year, but once you know what to look for, you can easily sidestep them and build a ton of confidence.

Let's break down the most common errors I see and how to make sure they don't happen to you.

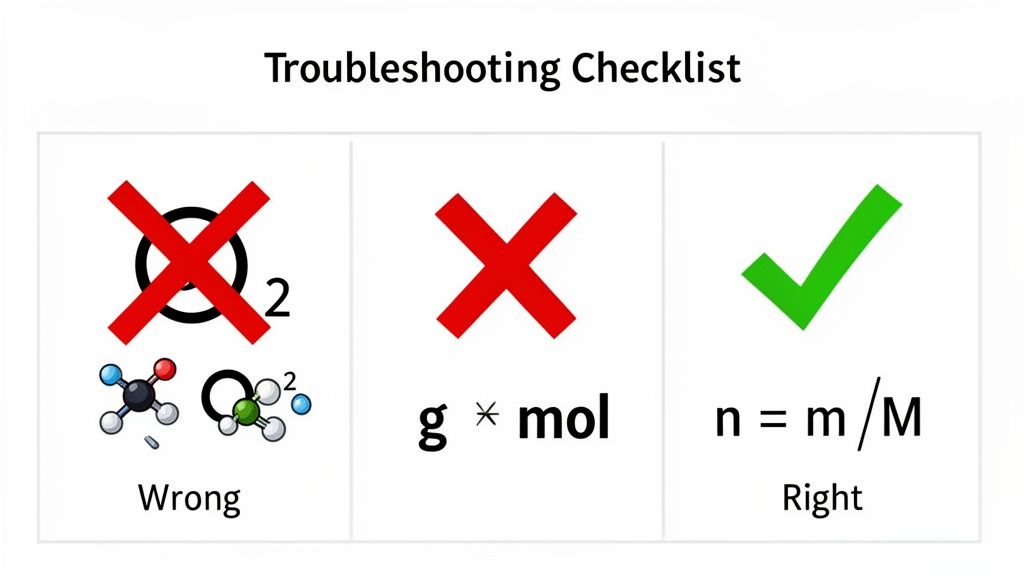
One of the sneakiest mistakes is mixing up atomic mass with molar mass for diatomic elements. It's an easy slip. For instance, a problem might mention oxygen gas. Your first instinct might be to just use the mass of a single oxygen atom (16.00 g/mol). But oxygen gas is O₂, so you actually need to use its true molar mass of 32.00 g/mol.

This one mistake will slice your final answer in half. Trust me, it's often the first thing instructors look for when grading. The same logic applies to any molecule with subscripts—every single one counts.

Getting Lost in Subscripts and Parentheses

Another frequent snag is dealing with complex formulas, especially those with parentheses, like magnesium nitrate, Mg(NO₃)₂. It’s tempting to just add up the masses of Mg, N, and three O's, but that little '2' outside the parentheses changes everything. It multiplies every single atom inside.

Here’s how to break it down correctly:

• Magnesium (Mg): You have 1 atom.
• Nitrogen (N): There's 1 atom inside the parentheses, but the subscript 2 on the outside means you have 2 total (1 × 2).
• Oxygen (O): You have 3 atoms inside, multiplied by that same subscript 2, giving you 6 total (3 × 2).

Forgetting that multiplier leads to a completely wrong molar mass, which throws off your entire calculation. You have to distribute that subscript. This skill is non-negotiable, especially as you move on to topics like stoichiometry. If you want more practice with this kind of detail work, our guide on how to balance chemical equations is a great next step.

My Pro Tip: Before you even touch a calculator, physically write down each element and the number of atoms you've counted. It’s a simple organizational step that prevents the vast majority of these calculation errors. It takes five extra seconds and saves a lot of headaches.

The Devil in the Details: Units and Sig Figs

Finally, let's talk about the small stuff that makes a big difference: units and significant figures (sig figs). If you don't track your units—making sure grams cancel out to leave you with moles—you can lose confidence in your setup. Always double-check that your units work out. It's your built-in error checker.

Significant figures can feel like a pain, but they're crucial. Your answer can't be more precise than your least precise measurement. It’s not just about getting points on a test; it reflects the reality of scientific measurement. Consider this: on recent AP Chemistry exams taken by over 162,000 US students, a whopping 35% of free-response questions required these exact conversions. Simple mistakes with significant figures were found to drop student scores by 15-20%.

To get this right, always look back at the mass you were given in the problem. The number of significant figures in that value dictates the number of sig figs your final answer should have. It's a small detail that shows you really know what you're doing.

Answering Your Top Questions About Mole Conversions

Let's tackle a few of the common questions that always come up when you're learning how to convert mass to moles. Nailing these concepts down will help everything click into place and make you much more confident when solving problems.

What's the Real Difference Between Atomic Mass and Molar Mass?

This is a big one, and it trips a lot of people up at first. It's all about scale.

Atomic mass is the mass of just one single atom of an element. It's measured in a ridiculously tiny unit called atomic mass units (amu). This is the number you find directly on the periodic table for each element.

Molar mass, however, is the mass of an entire mole (6.022 x 10²³ particles) of that same substance. Think of it as a "chemist's dozen"—it's a massive collection of atoms or molecules, and its weight is conveniently measured in grams per mole (g/mol).

The numbers might look the same (carbon's atomic mass is ~12.01 amu, and its molar mass is ~12.01 g/mol), but the concepts are worlds apart. One is the mass of a single atom, and the other is the mass of a huge, lab-sized pile of them.

For any mass-to-mole calculation you do, you will always use the molar mass in g/mol. This is your bridge between the grams you can weigh on a scale and the moles you need for chemical equations.

How Do I Go the Other Way and Convert Moles Back to Mass?

Great question. Working the calculation in reverse is just as crucial. You'll need this skill all the time, whether you're figuring out how much product a reaction should yield or measuring out chemicals to make a specific solution.

Luckily, it’s just a simple flip of the original formula. Instead of dividing the mass by the molar mass, you multiply the moles by the molar mass.

• Mass (g) = Moles (n) × Molar Mass (M)

Let's say a procedure asks you to use 2.5 moles of table salt, sodium chloride (NaCl). We already know its molar mass is about 58.44 g/mol. The math is straightforward:

Mass = 2.5 mol × 58.44 g/mol = 146.1 grams

That’s how you turn an abstract number of moles into a real-world quantity you can actually measure out.

Why Do My Teachers Care So Much About Significant Figures?

Ah, "sig figs." They can feel like a chore, but they're how scientists communicate how precise their measurements really are.

Think about it: weighing something on a lab balance that reads 15.00 g is much more precise than using a kitchen scale that just says 15 g. Significant figures carry that level of precision through your calculations. The rule of thumb is that your final answer can't be more precise than your least precise measurement.

In a classroom, getting your sig figs right is often required for full points because it proves you're thinking about the quality of your data. In a real lab, being sloppy with them could lead to inconsistent or incorrect results, which can have serious consequences. It's a small detail that shows you truly understand the practice of scientific measurement.

---

Stuck on a tricky chemistry problem or need a quick explanation? Feen AI can help. Snap a photo of your homework, upload a PDF, or just ask a question. Get clear, step-by-step solutions for chemistry, physics, math, and more. Stop guessing and start understanding with your personal AI homework helper.