A Chemist's Guide on How to Calculate Molar Mass

Calculating molar mass is pretty straightforward once you get the hang of it. You’re essentially just adding up the atomic masses of all the atoms in a chemical formula. Find each element, count its atoms using the subscripts, multiply that number by the element's atomic mass from the periodic table, and then sum it all up.

What Molar Mass Is and Why It Matters in Chemistry

Before we jump into the "how-to," let's quickly cover what molar mass actually is. Think of it as the crucial link between the microscopic world of atoms and the macroscopic world of grams that we can actually measure in a lab.

Molar mass is simply the mass of exactly one mole of a substance. We express it in grams per mole (g/mol).

Counting individual atoms is impossible—they're just too small and there are way too many of them. To get around this, chemists came up with a special unit called the mole. A mole is a specific, mind-bogglingly large number of particles: 6.022 x 10²³, a value known as Avogadro's number.

This unit lets chemists work with substances on a practical scale. Molar mass helps you answer real questions like, "If I weigh out 18 grams of water on the balance, how many actual H₂O molecules do I have?"

Building the Concept of Molar Mass

This big idea didn't just appear out of thin air. It started back in 1805 when John Dalton published one of the first tables of atomic weights, setting hydrogen's relative mass to 1. Chemists like Jöns Jakob Berzelius refined these tables through the mid-1800s.

A major breakthrough came in 1811 from Amedeo Avogadro, who proposed that equal volumes of gases have an equal number of particles. This idea was the seed that grew into the mole concept, a term Wilhelm Ostwald finally coined in 1893. Molar mass became the bridge connecting these relative atomic masses to tangible measurements in grams. You can explore more about the history of the mole concept and see how it evolved.

This is why getting a handle on molar mass is so important. It’s not just busywork; it's a core skill for pretty much everything else you'll do in chemistry.

Molar mass is your go-to chemical conversion factor. It lets you translate the mass of a substance you can physically weigh into the number of moles, which is the language chemists use for reactions and quantities.

The Practical Importance in Chemistry

So, why do you need to know this for your chemistry class or lab? Understanding molar mass is absolutely critical for a few key tasks:

• Stoichiometry: It's how you predict the amount of reactants you'll need or the products you'll get in a chemical reaction.
• Solution Preparation: You need it to figure out how many grams of a solid to dissolve to make a solution of a specific concentration, like molarity.
• Formula Determination: It helps you identify unknown substances by comparing their experimentally found molar mass to the mass of a proposed chemical formula.

In short, mastering this one skill is what unlocks your ability to do real, quantitative chemistry. It’s the tool that makes all those chemical equations truly useful.

Your Essential Toolkit for Molar Mass Calculations

Before you jump into any chemistry problem, it’s smart to get your gear in order. Luckily, for molar mass calculations, you only need two things: a good periodic table and a trusty calculator.

Think of it as setting up your workspace. Getting comfortable with these two simple tools is the first real step toward getting accurate answers and building confidence. It’s all about preventing those small, silly mistakes that can throw off a much bigger calculation later on.

Decoding the Periodic Table for Molar Mass

Your periodic table is basically a cheat sheet, but you have to know what you're looking for. Each little box is packed with info, but for molar mass, you can ignore almost all of it. Your eyes should go straight to one specific number: the atomic mass.

This number, usually found at the bottom of an element's square, is the key. It's the weighted average mass of that element's naturally occurring isotopes. The best part? The atomic mass value is numerically the same as the molar mass. Just swap the unit "amu" for "g/mol," and you're good to go.

To make sure you're grabbing the right number every time, here's a quick guide to what you'll see in a typical element's box.

Decoding the Periodic Table for Molar Mass

Information	What It Is	How to Use It
Atomic Number	The whole number, often at the top (e.g., 8 for Oxygen).	IGNORE THIS! It’s the proton count, not the mass.
Element Symbol	The one or two-letter code (e.g., O for Oxygen).	Use this to quickly locate your element on the table.
Atomic Mass	The decimal number, usually at the bottom (e.g., 15.999 for Oxygen).	THIS IS YOUR NUMBER! Use this value for your calculation in g/mol.

So, if you need the molar mass of a single carbon atom, you just find its box, grab the atomic mass (12.011), and write it down as 12.011 g/mol. It’s that direct.

Your Calculator Is Your Best Friend

You don't need a fancy graphing calculator; a basic scientific one will do just fine. The real skill isn't the calculator itself but how you use it. One of the most common trip-ups I see is students rounding their numbers too early.

Pro Tip: Always carry at least two decimal places for your atomic masses throughout the entire calculation. Rounding only at the very end will keep your answer precise and accurate.

Get comfortable with the parenthesis buttons. They are essential for keeping your calculations clean, especially with more complex compounds.

Let's say you're working with magnesium nitrate, Mg(NO₃)₂. You need to calculate the mass of the nitrate part (NO₃) first, then multiply it by two. Punching it into your calculator as (14.01 + 3 * 16.00) * 2 ensures the order of operations is correct. It saves you from easy-to-make errors and keeps your work organized.

Once you get the hang of the process, it's all about practice. Testing yourself with real exam questions from resources like VCE Chemistry past papers is a great way to solidify your skills. And if a problem has you totally stumped, a chemistry AI solver can walk you through the steps. With these tools and a bit of practice, you’re ready to tackle any molar mass problem that comes your way.

Calculating Molar Mass for Elements and Simple Compounds

Alright, let's put the theory into action. We’ll start with the basics—finding the molar mass of a single element—and then build up to simple compounds. The process is really just a system of addition and multiplication, so once you get the hang of it, you can apply it to nearly any chemical formula you come across.

Working with Single Elements

Calculating the molar mass for an individual element is the easiest place to start. In fact, it's less of a calculation and more of a quick lookup. You'll need this skill for every other problem, so it's a great foundation.

The molar mass of any element is just its atomic mass straight from the periodic table, but with the units swapped to grams per mole (g/mol). That’s it.

Here’s what that looks like in practice:

• Copper (Cu): Find copper on the periodic table. You'll see its atomic mass is around 63.546 amu. For our purposes, that means its molar mass is 63.546 g/mol.
• Helium (He): Now find helium. Its atomic mass is about 4.003 amu. So, the molar mass of helium is 4.003 g/mol.

This one-to-one relationship is our starting point for everything else. You're just translating the number on the periodic table into a value we can use in the lab.

The Method for Simple Compounds

Now, what happens when we combine elements to form a compound? The logic doesn't change much—we just need to account for the mass of every single atom in the formula. I have a simple mental checklist I run through every time.

1. Break it down: First, I identify every element in the formula.
2. Count them up: Then, I count how many atoms of each element are present, paying close attention to the subscripts.
3. Do the math: I multiply the atom count for each element by its molar mass from the periodic table.
4. Add it all together: Finally, I sum up the total masses of each element to get the final molar mass for the entire compound.

Following these steps ensures you don't miss anything. Let's try it with a couple of common examples.

A Quick Tip: The subscript in a chemical formula tells you the number of atoms for the element right before it. If you don't see a subscript, it’s understood to be one.

Example One: Finding the Molar Mass of Salt

Let’s calculate the molar mass for sodium chloride (NaCl), which you probably know as table salt. This is the perfect first example because it's a simple one-to-one compound.

• Identify & Count: The formula NaCl shows us we have one Sodium (Na) atom and one Chlorine (Cl) atom.
• Look up the Masses: From the periodic table, the molar mass of Na is 22.990 g/mol, and for Cl, it is 35.45 g/mol.
• Multiply & Sum:
  • (1 Na atom × 22.990 g/mol) = 22.990 g/mol
  • (1 Cl atom × 35.45 g/mol) = 35.45 g/mol
  • Total Molar Mass = 22.990 + 35.45 = 58.44 g/mol

So, one mole of table salt weighs 58.44 grams. Notice how we kept the decimal places from the periodic table? That's key for maintaining accuracy in your calculations.

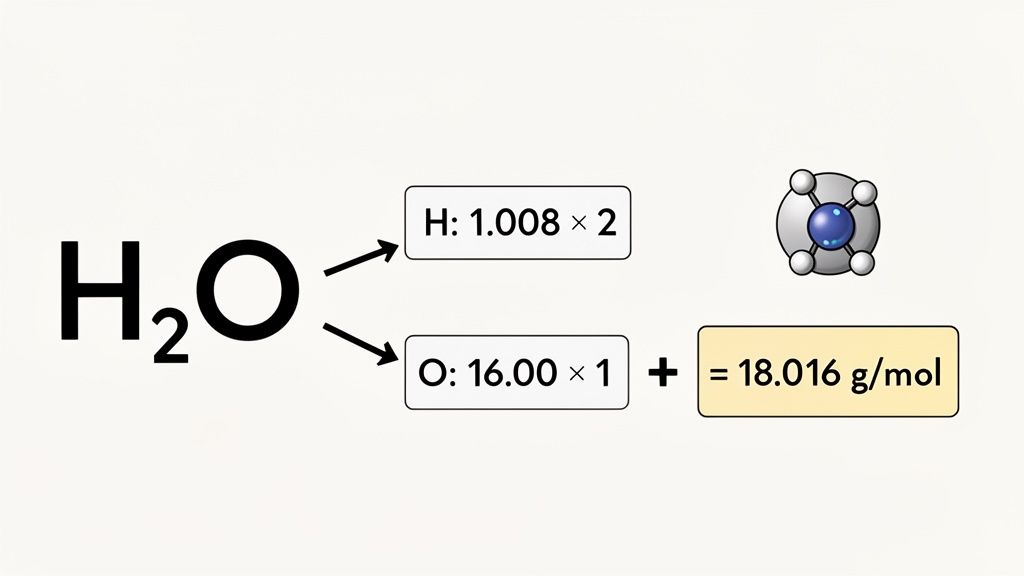
Example Two: Calculating the Molar Mass of Water

Next up is water (H₂O). This adds a small twist because of the subscript, which makes the atom count crucial.

• Identify & Count: The formula H₂O tells us we have two Hydrogen (H) atoms and one Oxygen (O) atom.
• Look up the Masses: Back to the periodic table, we find the molar mass of H is 1.008 g/mol and for O, it is 16.00 g/mol.
• Multiply & Sum:
  • (2 H atoms × 1.008 g/mol) = 2.016 g/mol
  • (1 O atom × 16.00 g/mol) = 16.00 g/mol
  • Total Molar Mass = 2.016 + 16.00 = 18.016 g/mol

This straightforward process is the engine behind all kinds of more advanced chemical calculations. Getting comfortable with these steps is essential for taking on multi-step problems later on.

If you want to see how these skills are used in bigger-picture scenarios, working through some guided stoichiometry practice problems with answers is a fantastic next step. This foundational skill directly connects to predicting the outcomes of chemical reactions, making it one of the most practical tools in your chemistry toolkit.

How to Handle Complex Compounds Like a Pro

Once you've got the hang of simple compounds, it’s time to move on to the formulas that look a bit more intimidating. When you first see chemical formulas with parentheses or dots, they can seem confusing, but the method for finding their molar mass is exactly the same. We just need to be extra careful when counting the atoms.

These aren't just for advanced chemistry, either. You’ll see them pop up constantly in high school and intro college courses. Getting good at these is a huge step toward being able to solve any molar mass problem that comes your way.

Tackling Compounds with Parentheses

You'll often run into formulas with a group of atoms in parentheses followed by a subscript, like magnesium nitrate, Mg(NO₃)₂. This is how we write compounds that contain polyatomic ions—basically, groups of atoms that act as a single unit with an overall charge.

The trick is to treat the subscript outside the parentheses just like the distributive property in math. That number applies to every single element inside the parentheses.

Let's walk through calculating the molar mass for magnesium nitrate, Mg(NO₃)₂.

• First, we need a solid atom count.

  • Magnesium (Mg): There's no subscript on Mg, so we have 1 atom.
  • Nitrogen (N): Inside the parentheses, N has an implied subscript of 1. The 2 outside applies to it, so we have 1 × 2 = 2 nitrogen atoms.
  • Oxygen (O): Oxygen has a subscript of 3 inside, which gets multiplied by the 2 outside. That gives us 3 × 2 = 6 oxygen atoms.

• Next, grab the molar masses from the periodic table.

  • Mg = 24.305 g/mol
  • N = 14.007 g/mol
  • O = 16.000 g/mol

• Now, we just multiply and add it all up.

  • Magnesium: 1 × 24.305 g/mol = 24.305 g/mol
  • Nitrogen: 2 × 14.007 g/mol = 28.014 g/mol
  • Oxygen: 6 × 16.000 g/mol = 96.000 g/mol

Adding these together, we get a total molar mass of 24.305 + 28.014 + 96.000 = 148.319 g/mol.

See? It's just one extra multiplication step. Forgetting to distribute that outer subscript is probably the most common mistake students make, so always double-check your atom count before you go any further. This skill is also crucial when you need to find the empirical formula for ascorbic acid or other molecules where getting the atom ratios right is everything.

Decoding Hydrated Salts

Another type of formula you’ll encounter is for hydrated salts, like copper(II) sulfate pentahydrate, CuSO₄·5H₂O. These are ionic compounds that have a specific number of water molecules physically trapped within their crystal structure.

That dot (·) in the middle looks weird, but it just means "add." You calculate the molar mass of the main salt (the CuSO₄ part) and then add the total mass of all the water molecules (the 5H₂O part) to it.

Key Insight: Don't mistake the dot (·) in a hydrated salt for a multiplication sign. It's a chemical notation telling you the water molecules are attached, so you simply add their mass to the rest of the compound.

Let’s run the numbers for CuSO₄·5H₂O. It's easiest to break this into two parts.

Part 1: The Salt (CuSO₄)

• Atoms: We have 1 Cu, 1 S, and 4 O.
• Molar Masses: Cu = 63.546 g/mol, S = 32.06 g/mol, O = 16.000 g/mol
• Mass of CuSO₄: (1 × 63.546) + (1 × 32.06) + (4 × 16.000) = 159.606 g/mol

Part 2: The Water (5H₂O)

• Atoms: The coefficient 5 applies to the whole H₂O molecule. This gives us 5 × 2 = 10 H atoms and 5 × 1 = 5 O atoms.
• Molar Masses: H = 1.008 g/mol, O = 16.000 g/mol
• Mass of 5H₂O: (10 × 1.008) + (5 × 16.000) = 10.080 + 80.000 = 90.080 g/mol
• Pro Tip: A faster way is to find the mass of one water molecule (18.016 g/mol) and just multiply by 5. You get the same answer: 5 × 18.016 = 90.080 g/mol.

Part 3: Combine Them

• Total Molar Mass = 159.606 g/mol (from CuSO₄) + 90.080 g/mol (from 5H₂O) = 249.686 g/mol

Tackling each part of the formula separately before adding them up is a great way to keep your work organized and avoid simple mistakes.

Dodging Common Pitfalls in Your Molar Mass Calculations

It happens to the best of us. You're cruising through a calculation, feeling confident, and then a tiny slip-up leads to the wrong answer. Knowing where the common traps are is the best way to sidestep them entirely. This isn't about scolding mistakes; it's about building the solid, reliable habits that get you to the right number, every single time.

Let's walk through the most frequent errors I see students make and, more importantly, how to avoid them. Think of this as your personal troubleshooting guide for molar mass.

Mistaking Atomic Number for Atomic Mass

This is, without a doubt, the number one mistake. When you're in a rush, your eyes can easily grab the wrong number from an element's box on the periodic table. The atomic number—that big whole number at the top (8 for Oxygen, for instance)—tells you the proton count. That's not what we need here.

For molar mass, you have to use the atomic mass, which is the decimal number, usually found at the bottom of the box (like 15.999 for Oxygen).

A Tale of Two Numbers
Let's take Carbon Monoxide (CO):

• Wrong: Using atomic numbers (Carbon's 6 + Oxygen's 8) gives you 14 g/mol. That's way off.
• Right: Using atomic masses (Carbon's 12.011 + Oxygen's 15.999) gives you the correct molar mass: 28.01 g/mol.

Make it a habit to always double-check that you're using the decimal value. It's a tiny detail that makes all the difference.

Forgetting to Distribute Subscripts Through Parentheses

When you see a formula with parentheses, like in calcium nitrate, Ca(NO₃)₂, that little subscript hanging on the outside acts as a multiplier for everything inside the parentheses. It’s easy to forget, but skipping this distribution step will completely throw off your atom count and guarantee an incorrect answer.

This flowchart breaks down how to approach these more complex formulas step-by-step.

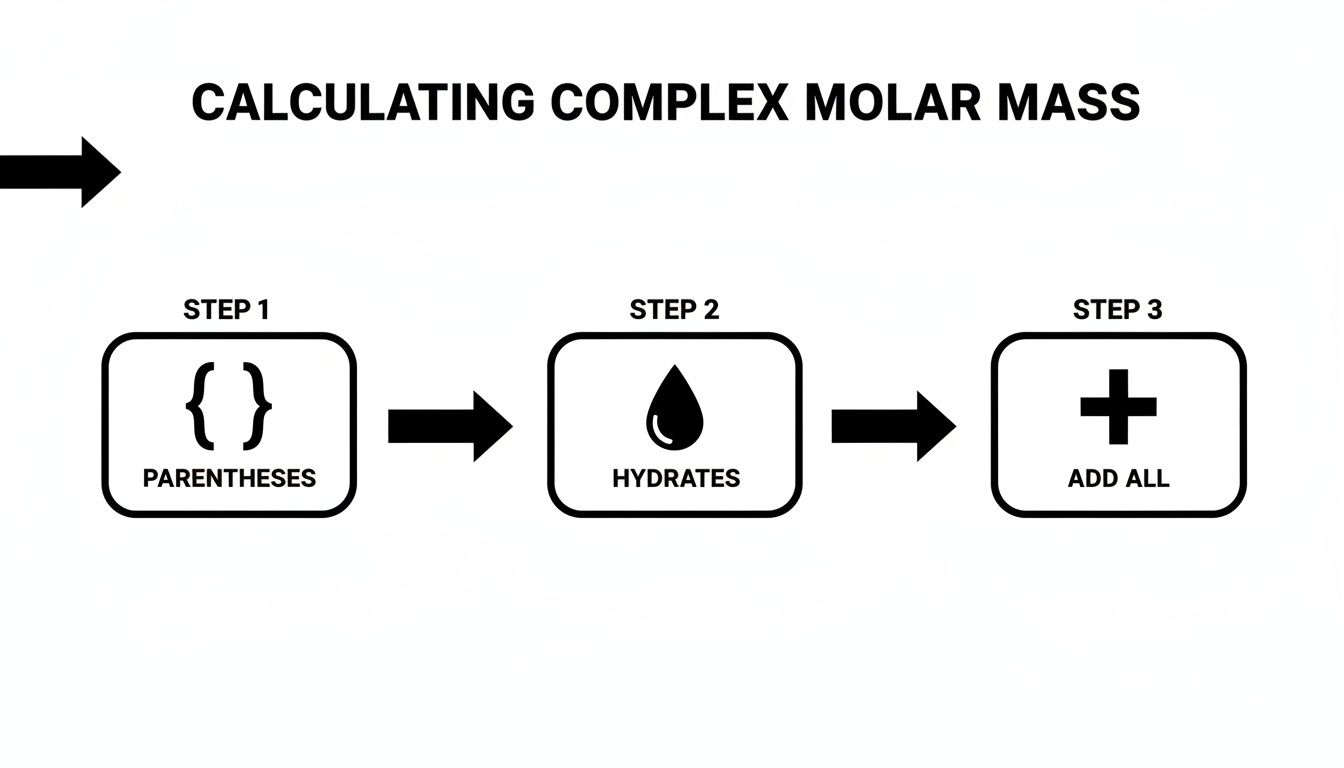
As you can see, tackling parentheses is one of the very first checks you should make.

Let's break down the atom count for Ca(NO₃)₂ one more time:

• Calcium (Ca): Just 1 atom. Easy enough.
• Nitrogen (N): There's 1 N inside, multiplied by the 2 outside, giving us 2 atoms total.
• Oxygen (O): We have 3 O's inside, and that also gets multiplied by the 2 outside, for a total of 6 atoms.

If you forget to distribute that "2", you'd end up using counts of 1 N and 3 O's, which sends the whole calculation sideways. Always handle what's in the parentheses first.

Rounding Your Numbers Too Early

I get it. It’s so tempting to round atomic masses to clean up the math. Why use 35.45 g/mol for Chlorine when 35 is right there? Because precision matters. A lot.

That small rounding difference might seem insignificant at first, but in a compound with several chlorine atoms, that tiny error gets multiplied. Suddenly, your final answer could be off by several grams per mole. On an exam, that's the difference between right and wrong. In a lab, it could mean a ruined experiment.

A Pro Tip I Swear By: I never round the atomic masses I pull from the periodic table. I carry at least two decimal places for every element all the way through the calculation. The only time I round is at the very end, and only to the number of significant figures my professor or lab manual requires.

This one habit will protect your accuracy from start to finish.

Treating the Hydrate Dot Like a Multiplication Sign

Last but not least, let's talk about hydrated salts, like copper(II) sulfate pentahydrate, CuSO₄·5H₂O. That centered dot can be deceiving. It looks a lot like a multiplication symbol, but in the language of chemistry, it means "add." It tells us that five water molecules are physically attached to the copper sulfate crystal.

So, when you see that dot, think ADDITION.

1. First, calculate the molar mass of the main salt (the CuSO₄ part).
2. Next, calculate the total mass of all the water molecules (in this case, 5 × the mass of H₂O).
3. Finally, add those two results together.

Never, ever multiply them. Keeping these common blunders in mind will help you build a much more precise and methodical approach, so you can calculate molar mass with confidence.

Common Questions About Molar Mass

Once you get the hang of calculating molar mass, you start running into those tricky edge cases or nagging questions. It's totally normal. Things like weird terminology or special situations can throw anyone for a loop at first.

Let's walk through some of the most common points of confusion. Nailing down these details will really cement your understanding and make you a lot more confident when you're doing your calculations.

What’s the Real Difference Between Molar Mass and Molecular Weight?

This is a great question. You’ll hear these terms thrown around interchangeably all the time, but there's a subtle yet important technical difference that’s good to know.

• Molecular Weight is all about the tiny stuff. It’s the mass of a single molecule, and we measure it in atomic mass units (amu). Think of it as the microscopic view.
• Molar Mass is what we use in the real world, like in a chemistry lab. It’s the mass of one mole (6.022 x 10²³ particles) of a substance, and its units are grams per mole (g/mol).

The numbers themselves are actually the same. A single water molecule (H₂O) has a molecular weight of about 18.02 amu. A whole mole of water has a molar mass of about 18.02 g/mol.

For most high school and first-year chemistry courses, you can pretty much treat them as the same concept. The most important thing is to get the units right. If the question asks for molar mass, your answer better have g/mol at the end of it.

How Do I Handle Isotopes When Calculating Molar Mass?

I have some good news for you: you don't have to do anything! The periodic table has already done the heavy lifting.

The atomic mass you see for an element on the table is a weighted average of all its naturally occurring isotopes. For example, chlorine exists as chlorine-35 and chlorine-37. The number on the periodic table, around 35.45 amu, is calculated based on how common each of those isotopes is in nature.

So, when you use 35.45 g/mol for chlorine in a calculation, you’re already accounting for the isotopic mix. The only time you'd ever need to calculate a weighted average yourself is if a problem specifically gives you the isotopic masses and their percent abundances and asks you to find the average atomic mass.

Is It Okay to Just Round Atomic Masses to Whole Numbers?

It’s definitely tempting to round things off to make the math easier, but you really should resist the urge. For your calculations to be accurate, it’s crucial to use the more precise values from the periodic table—usually to at least two decimal places.

Let's look at an example with dichlorine heptoxide (Cl₂O₇).

• Rounding: (2 × 35) + (7 × 16) = 70 + 112 = 182 g/mol
• Using precise values: (2 × 35.45) + (7 × 16.00) = 70.90 + 112.00 = 182.90 g/mol

That difference of 0.90 g/mol might not seem like a big deal. But when you're doing longer problems with multiple steps (like in stoichiometry), these small rounding errors can build up and throw your final answer way off.

My personal rule of thumb is to always carry at least two decimal places for atomic masses all the way through a problem. Only round your final answer to the correct number of significant figures at the very end. It's a simple habit that will save you from losing points.

---

Struggling with a tricky chemistry problem or need a step-by-step explanation for your homework? With Feen AI, you can get instant help by simply uploading a picture of your assignment. Get clear solutions and conquer your coursework at https://feen.ai.