How to Solve Probability Problems A Practical Guide

Before you can solve any probability problem, you have to get your hands dirty with the setup. It’s a simple, three-part process: first, figure out every single thing that could happen (that's your sample space). Next, pinpoint the specific outcome you actually care about (the event). Only then can you pick the right tool from your mathematical toolbox to find the answer.

Your Framework for Solving Probability Problems

Probability can feel intimidating, but there's a reliable method to crack just about any problem thrown your way. The big secret? Don't jump straight into the numbers. The smartest students I've seen are the ones who take a breath and logically map out the problem first. Get the setup right, and the calculations often take care of themselves.

Think of this framework as a mental checklist. It forces you to slow down and catch the little details hidden in the wording of a question. Trust me, most students get tripped up not because the math is hard, but because they misunderstood what the question was truly asking. Breaking it down into these core components gives you a clear roadmap to the solution. To really master this, it helps to understand the fundamental theories of learning that shape how we build new problem-solving skills.

Here’s a quick reference table that breaks down the three essential first steps. I tell my students to internalize this process until it becomes second nature.

The Three Foundational Steps to Solving Any Probability Problem

Step	Action	Why It Matters
1. Understand the Universe	Identify and list all possible outcomes. This is your Sample Space (S).	An incomplete or incorrect sample space is the most common source of error. It forms the denominator of your probability fraction.
2. Define the Target	Clearly state the specific outcome(s) you are interested in. This is your Event (E).	Ambiguity here leads to wrong calculations. You must know exactly what counts as a "successful" outcome.
3. Choose Your Tool	Select the appropriate probability rule, formula, or technique based on the problem's structure.	Using the wrong formula (e.g., addition instead of multiplication) is a frequent mistake. The setup guides your choice.

This process isn't just about following rules; it’s about translating a word problem into a clean, structured mathematical question. Let's dig into why each of these steps is so non-negotiable.

Breaking Down the Core Steps

• Define the Sample Space (S): This is your entire universe of possibilities. If you're flipping a coin, the sample space is {Heads, Tails}. If you're drawing a card from a standard deck, it’s all 52 cards. Get this wrong, and your entire calculation will be flawed from the start.

• Identify the Event (E): Now, narrow your focus. What specific result are you measuring? The event might be "flipping heads" or "drawing a King." Be precise. "Drawing a King" is a very different event from "drawing a red King."

• Select the Right Method: With a crystal-clear sample space and event, you can finally pick your weapon. Is this a simple case where Probability = (Favorable Outcomes) / (Total Outcomes)? Or does it involve multiple stages, making a tree diagram a better fit? Maybe it's a tricky "at least one" scenario where using the complement is the smart move. The setup tells you which tool to grab.

By following these steps, you turn confusing, abstract questions into concrete, solvable puzzles. If you want to dive deeper into building these analytical skills, our guide on https://feen.ai/blog/how-to-solve-math-problems-step-by-step is a great place to start.

My Pro Tip: The biggest mistake I see students make is rushing the setup. Seriously, spend 80% of your time defining the sample space and the event. The calculation itself should only take up 20% of your effort. This one shift in focus will boost your accuracy more than anything else.

Mastering the Core Concepts of Probability

Before you can jump into tricky problems, you absolutely have to nail the fundamentals. Probability is more than just plugging numbers into formulas; it's a whole way of thinking about uncertainty. Honestly, building a solid foundation here is the single most important thing you can do.

And look, you're not alone if you find this stuff tough. A major study focusing on undergrad stats students showed just how common it is to struggle with probabilistic reasoning. It's a global issue in higher education, which is exactly why getting the basics right is so critical. The full research paper offers some really interesting insights into these learning challenges.

Let's walk through the core ideas you'll need, using examples you can actually picture.

Sample Spaces and Events: The Building Blocks

First up is the sample space. This sounds technical, but it’s just a fancy term for the complete list of every single thing that could possibly happen in an experiment. If you roll a standard six-sided die, the sample space is simply {1, 2, 3, 4, 5, 6}. That's it. Nothing else is possible.

From there, we have an event, which is just the specific outcome (or group of outcomes) you care about. Sticking with our die, an event might be "rolling an even number." That specific event is the subset {2, 4, 6} from our sample space.

The most fundamental formula in probability ties these two concepts together.

Probability of an Event = (Number of Favorable Outcomes) / (Total Number of Possible Outcomes)

For our event of rolling an even number, there are 3 outcomes we want ({2, 4, 6}) out of a total of 6 possible outcomes. So, the probability is 3/6, which simplifies to 50%. This simple fraction is truly the heart of probability.

Diving Deeper: Conditional Probability and Independence

Now for where things get more interesting—when one event can affect another. This is the world of conditional probability, which asks, "What's the probability of A happening, assuming B has already happened?" You'll see this written as P(A|B).

Imagine you have a standard deck of 52 cards. You pull one out and see it's a King. What's the probability that the next card you draw is also a King? Well, the situation has changed. There are now only 3 Kings left in a deck of 51 cards. The probability is different because of that first draw.

This leads us right to the idea of independence. Two events are independent if the outcome of one has absolutely no impact on the outcome of the other.

• Independent Events: Think about flipping a coin twice. Getting heads on the first flip doesn't change the 50/50 odds for the second one.
• Dependent Events: Drawing two cards from a deck without putting the first one back is a classic example. The first card you draw directly changes the probabilities for the second.

Getting this distinction right is crucial because it tells you which formula to use. It's the difference between a simple multiplication rule and the more complex conditional probability formula. Being able to spot the difference is half the battle. While we're on core statistical ideas, understanding variance is also a must-know. You can get a good breakdown in our guide on how to calculate standard deviation.

Once you've got these definitions down—sample space, event, conditional probability, and independence—you have the language and the framework to tackle almost any question. When you can accurately describe a problem using these terms, you're already halfway to the solution.

Building Your Problem-Solving Toolkit

Knowing the core concepts of probability is like having a toolbox full of shiny new tools. That’s a great start, but now you have to learn how to actually use them. Solving probability problems is all about picking the right tool for the job. It's where the abstract theory gets its hands dirty with practical application.

You wouldn't use a sledgehammer to hang a picture, right? The same logic applies here. Sometimes a quick sketch or a tree diagram will get you to the answer faster and more reliably than a complicated formula. The goal is to build a flexible set of techniques you can pull from depending on what the problem throws at you.

Visualizing with Probability Trees

When a problem breaks down into a sequence of events, a probability tree is your absolute best friend. Seriously. It’s a fantastic way to turn a confusing word problem into a simple, visual map.

Each branch on the tree represents a possible outcome, and you just label it with its probability. To figure out the chances of a specific sequence happening, you just multiply the probabilities along that specific path.

Let's use a classic example: A bag has 3 red and 2 blue marbles. You pull one out, leave it out, and then grab a second. What’s the probability you draw two red marbles in a row?

• Your first draw splits into two main branches: "Red" (with a probability of 3/5) and "Blue" (2/5).
• Now, follow the "Red" branch. Since you didn't replace the first marble, the bag now only has 2 red and 2 blue marbles left. The probability of drawing another red is now 2/4.
• To get the probability of "Red then Red," just multiply down that path: (3/5) * (2/4) = 6/20, which simplifies to 0.3 or 30%.

Probability trees make conditional probability feel much more intuitive because you can literally see how each event changes what can happen next.

Counting Smarter with Combinatorics

So, what happens when the number of possible outcomes is huge—too big to list out or draw in a tree? This is where combinatorics, the art of clever counting, saves the day. You'll mainly run into two big ideas: permutations and combinations.

• Permutations: Use these when the order of selection matters. Think of arranging books on a shelf, setting a batting order for a baseball team, or assigning specific roles like President and VP.
• Combinations: Use these when the order doesn't matter. This is perfect for situations like picking a few people for a committee (where everyone's role is the same) or drawing a hand of cards for poker.

Mixing these two up is a super common mistake. The easiest way to keep them straight is to ask yourself one simple question: "If I rearranged the items I picked, would it count as a different outcome?" If the answer is yes, you need permutations. If no, you're dealing with combinations. To really hone these analytical skills, it’s worth taking time to develop problem-solving skills in a structured way.

The Power of the Hypothetical 1,000 Method

Conditional probability problems, especially those involving medical test results or weird percentages, can be a real headache. Instead of wrestling with the formal Bayes' Theorem, there’s a brilliantly simple trick that makes these problems feel way more concrete.

It’s often called the "hypothetical 1,000" method. You just imagine a population of 1,000 people and use the percentages from the problem to fill out a quick frequency table. It's a fantastic way to build intuition because you're working with real-seeming numbers instead of abstract formulas.

Let’s see it in action: A rare disease affects 1% of the population. A test for it correctly identifies 99% of people who have it, but it has a 5% false positive rate (meaning 5% of healthy people test positive). If someone tests positive, what’s the actual chance they have the disease?

Instead of diving into a formula, let's start with 1,000 people.

• People with the disease: 1% of 1,000 = 10 people.
• People without the disease: The other 990 people.

Now, who tests positive?

• True Positives: The test catches 99% of the 10 sick people, so that's 9.9 people (we can round to 10).
• False Positives: The test incorrectly flags 5% of the 990 healthy people, which is 49.5 people (we can round to 50).

So, in total, we have 10 + 50 = 60 people who tested positive. But out of those 60, only 10 actually have the disease. The probability is therefore 10/60, or about 16.7%. This approach is often far more intuitive and less prone to simple calculation errors than the pure formula. This kind of reasoning is a foundational step toward more formal statistical methods. If you're curious about where this leads, you can check out our guide on https://feen.ai/blog/what-is-hypothesis-testing-in-statistics to see how these ideas connect.

Tackling Common Probability Problems Head-On

Theory is great, but probability really clicks when you start getting your hands dirty. This is where we'll walk through some of the most common types of problems you'll see on homework and exams. We’re not just chasing answers; we're building a repeatable process for breaking down any probability question that comes your way.

The first, and most important, move is to figure out what kind of problem you're looking at. Are you just counting outcomes? Do events depend on each other? Is new information changing the odds? This quick mental flowchart can be a lifesaver.

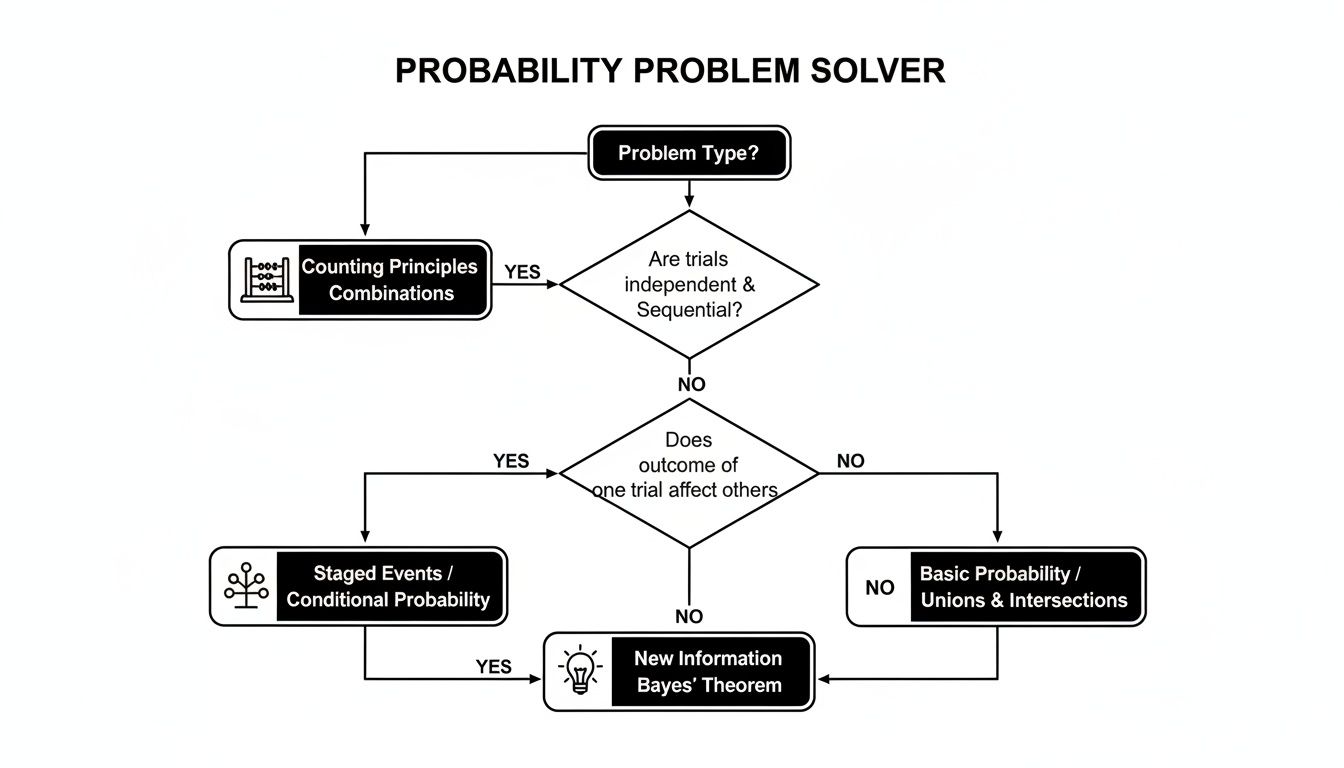
As you can see, once you diagnose the problem, you've already got a clear path toward the right technique.

With and Without Replacement Problems

These are the bread and butter of probability 101, usually involving drawing marbles from a bag or cards from a deck. The whole game changes based on one little detail: do you put the item back after you draw it? That single action determines if your events are independent or dependent.

Example 1: Marbles Without Replacement

Imagine a bag with 5 red marbles and 3 blue marbles. You're asked to draw two marbles, one after the other, without putting the first one back. What’s the probability both are red?

Let’s think this through. The probability of the first marble being red is pretty straightforward: there are 5 red marbles out of 8 total, so 5/8.

But for the second draw, the situation has changed. Assuming you drew a red one first, there are now only 4 red marbles left, and only 7 total marbles in the bag. So, the probability of the second one also being red is 4/7.

To get the probability of both things happening in sequence, we just multiply the individual probabilities: (5/8) × (4/7) = 20/56

This simplifies down to 5/14, or about 35.7%.

Key Takeaway: When you see "without replacement," your brain should immediately scream "dependent events!" The denominator (and possibly the numerator) of your fraction will change with every single draw.

Binomial Probability Problems

These questions always have a specific flavor. You're running a set number of trials, and each trial only has two possible outcomes—success or failure. Think flipping a coin ten times, a basketball player shooting five free throws, or a factory checking parts for defects.

Example 2: Basketball Free Throws

Let's say a basketball player has a solid free-throw record, making 80% of their shots. If they take 5 shots in a game, what's the probability they make exactly 4 of them?

This is a classic binomial scenario. We have a fixed number of trials (n=5), each shot is independent, there are two outcomes (make or miss), and the probability of success is constant (p=0.8). We're looking for exactly k=4 successes.

This calls for the binomial probability formula: P(k successes in n trials) = C(n, k) * p^k * (1-p)^(n-k).

First, how many different ways can the player make 4 out of 5 shots? They could miss the first, the second, the third, etc. This is a combination problem, C(5, 4), which is 5.

Now, we just plug all the numbers into the formula: P(4 makes) = C(5, 4) × (0.8)⁴ × (0.2)¹ P(4 makes) = 5 × (0.4096) × (0.2) P(4 makes) = 0.4096, or 40.96%.

So, there's just under a 41% chance our player sinks exactly four of their five shots.

Conditional Probability with Real Data

Often, you'll get a problem that throws a table of data at you. These questions test whether you can correctly narrow your focus based on a specific condition. The phrase "given that" is your signal to ignore most of the data.

Example 3: Survey Data Analysis

A university surveys 200 students about their preferred morning drink, with the results broken down by class year.

	Coffee	Tea	Total
Seniors	60	20	80
Juniors	40	80	120
Total	100	100	200

The question is: What is the probability that a student prefers coffee, given that they are a senior?

That "given that" part is crucial. It means we're no longer concerned with all 200 students. Our entire universe has shrunk to just the 80 seniors. This is our new denominator.

Within that group of 80 seniors, how many prefer coffee? The table tells us it's 60.

So, the probability is simply 60 / 80, which simplifies to 3/4 or 75%.

These examples show that a systematic approach is your best friend. By first identifying the problem type and then applying the right tools, you can break down even the most intimidating questions into manageable pieces.

How to Avoid Common Pitfalls and Mistakes

Even the most careful students get tripped up by probability. It's rarely the big, complicated formulas that are the problem. Instead, it's the small, subtle misunderstandings that snowball into completely wrong answers.

Honestly, learning to recognize these common traps is one of the best ways to get better, fast. Most of the time, the mistake happens right at the beginning, when you try to turn the word problem into math. If you can nail that translation, you're already halfway to the right answer.

Forgetting That Order Matters (Sometimes)

One of the most common mix-ups I see is between permutations and combinations. Both are about counting groups, but they answer very different questions. The entire difference boils down to one thing: does the order you pick things in create a new outcome?

• Permutations: This is for when order is critical. Think about arranging books on a shelf, setting a combination lock, or assigning specific roles like president and vice-president. Swapping the order gives you a totally different result.
• Combinations: Here, order is completely irrelevant. This is what you use for picking a team for a project or drawing a hand of cards. A hand with an Ace and a King is the same hand, regardless of which one you picked up first.

When you're stuck, just ask yourself this simple question: "If I rearrange the items I chose, do I have a new outcome?" If the answer is yes, you're dealing with permutations. If it's no, it's all about combinations.

Misinterpreting "And" vs. "Or"

Another classic mistake is fumbling the multiplication and addition rules. These are tied directly to the words "and" and "or," and getting them straight is crucial.

• "And" almost always means multiply. When you need Event A and then Event B to happen, you multiply their probabilities. This is for sequences, like drawing a king from a deck and then drawing a queen.

• "Or" almost always means add. When you want to find the chance of either Event A or Event B happening, you add their probabilities. This is for figuring out the probability of one of several possibilities, like drawing a king or a queen on a single draw.

My Pro Tip: Be super careful with "or" problems. You always have to check for overlap. If you're asked for the probability of drawing a King or a Spade, you can't just add them up. You have to subtract the probability of the King of Spades because you've counted it twice. It's a small detail that makes a huge difference.

Assuming Independence When It Isn't There

It’s so tempting to assume events are independent. The math is just so much easier! But this is a dangerous shortcut that often leads to the wrong answer.

Two events are only independent if the outcome of one has absolutely no impact on the outcome of the other. Flipping a coin twice is the textbook example of independence.

But so many problems involve dependent events. Drawing two cards from a deck without replacement is the classic scenario here. The first card you take out fundamentally changes the deck—the sample space—for the second draw. That, in turn, changes the probability.

Always take a second and ask yourself, "Does the first thing that happens change the odds for the second thing?" If it does, you're working with conditional probability.

Research backs this up—how you learn to approach these problems really matters. Studies have found that focusing on identifying these common misconceptions, instead of just memorizing formulas, leads to much better results. You can discover more insights about how teaching methods impact student success in probability. By actively looking for these mistakes in your own work, you're not just solving a problem; you're building a much more reliable way of thinking.

Frequently Asked in Probability

Once you’ve got the basic rules down, the real challenge begins: actually solving problems. This is where the theory meets the road, and it’s completely normal to have a ton of questions. Let's dig into some of the most common things students ask when they’re trying to make that leap from just understanding the formulas to actually using them to get the right answer.

Think of this as the practical advice you wish you had when you're staring at a tough problem set late at night. We're not introducing new formulas here. Instead, we’re focused on smart strategies to make probability feel less like a guessing game and more like a puzzle you know how to solve.

What Is the Best Way to Practice Probability Problems?

Just doing a ton of problems isn't the secret. The real key is mixing it up and being deliberate about how you review your work. I always tell my students to start with the foundational problems in their textbook to make sure the core concepts are solid. After that, branch out. Look for online worksheets or practice sites to see how the same ideas can be phrased in totally different ways.

This next part is crucial: After you solve something, always go back and review the official solution. Do this even if you got it right. Why? Because there’s often a more elegant or efficient way to get to the answer, and seeing those alternative methods is how you build a real toolkit of problem-solving skills.

Here's a pro-tip that works wonders: try to explain how to solve a tough problem to a friend. If you can teach it, you’ve truly mastered it. This simple act forces you to organize your logic and instantly reveals any weak spots in your understanding.

How Can I Get Better at Word Problems in Probability?

Ah, word problems. They’re usually the biggest hurdle because they’re really a test of translation, not just math. My advice is to stop trying to solve the problem on your first read. It just creates panic.

Instead, develop a system. First, just read the problem to get the story. Are we dealing with cards, coins, or medical tests? Next, read it again, but this time with a pen or highlighter in hand. Circle or underline key numbers and, more importantly, the magic words. Phrases like “at least,” “exactly,” “given that,” or “without replacement” are huge signals pointing you toward the right formula.

Once you’ve pulled out the key info, your job is to turn those English phrases into math. For instance, "the probability of A happening, given that B already happened" is just P(A|B). Drawing a quick tree diagram or sketching out a 2x2 table is also a lifesaver for organizing the information before you even think about plugging numbers into a formula.

Are There Any Tools That Can Help Me Learn Probability?

Absolutely. We've come a long way from just having a standard calculator. There are some fantastic online graphing tools that can help you visualize things like a normal distribution, which makes abstract concepts much more concrete. You can also find countless educational websites with interactive quizzes to get instant feedback on your skills.

For direct help with your homework, an AI-powered tool is your best bet. It can give you a full, step-by-step breakdown of a solution, not just the final answer. This is incredibly useful for checking your work, but more importantly, for figuring out where you went wrong when you get stuck. Think of it as a 24/7 study partner that can help you understand the logic.

What Is the Difference Between Conditional Probability and Independent Events?

This is a big one, and it trips a lot of people up. They sound similar, but they're fundamentally different.

Independent events have zero effect on each other. The outcome of one has no bearing on the outcome of the other. The classic example is flipping a coin and then rolling a die. The coin landing on heads doesn't change the 1/6 probability of rolling a four.

Conditional probability, however, is all about dependent events—situations where one outcome directly changes the probability of the next. Imagine drawing a card from a deck and not putting it back. That first draw changes the entire deck (there are now only 51 cards), so the odds for the second draw are different. The formula P(A|B) is how we calculate the new probability of A, now that we know B has already occurred.

---

Feeling stuck on a problem or just want to double-check your work? Feen AI is designed to help you understand the how and why behind the answer. You can upload a picture of your homework, get step-by-step solutions, and ask follow-up questions until the concept clicks. Stop staring at problems and start solving them with confidence.