How to Solve Word Problems in Algebra

Cracking algebra word problems is all about translating a story into a solvable equation. The secret isn't being a math genius; it's about having a solid, repeatable process. You need to read carefully, figure out what you're solving for, build the equation, and then solve and check your work. This structured approach cuts through the confusion and lays out a clear path to the answer.

Why Do Algebra Word Problems Feel So Tough?

Staring at a wall of text mixed with numbers can be intimidating. If you feel a little stressed when you see one, you're definitely not alone. The real challenge isn't usually the algebra itself—it's the translation. You have to be a detective first, pulling out the crucial information from the story, and then be a mathematician to put it all together.

This isn't just a feeling; it's a well-known hurdle in learning math. Research has shown for years that students struggle with this translation process, even from a very young age. In some studies, certain types of word problems were solved correctly by less than 50% of first-graders. This shows just how tricky it is to turn language into math right from the start. You can find more about this on Symbolab's word problem calculator page.

The great news is that this is a skill, not an innate talent. Like any skill, you can master it with the right strategy. The key is to stop trying to solve everything at once and instead follow a framework that breaks the problem down into manageable pieces.

A Framework for Turning Confusion Into Clarity

Instead of getting overwhelmed, let's treat every word problem like a puzzle. I use a simple "4-D" framework that gives you an actionable plan for any problem you face.

• Decode: First, just read. What's the story here? What do you know for sure, and what are they asking you to find? Don't even think about math yet—just understand the situation.
• Define: Now, pinpoint the main unknown. This is what you're trying to figure out. Give it a name, usually a variable like x or y. This is the anchor for your entire equation.
• Develop: With your variable in place, start building the equation. Translate the relationships and quantities from the story into a mathematical sentence. This is where "twice a number" becomes 2x or "five less than" becomes x - 5.
• Deduce: Finally, it's time to do the math. Solve the equation for your variable. But don't stop there! Plug your answer back into the original problem to make sure it actually makes sense in the context of the story.

This simple, sequential flow keeps you on track.

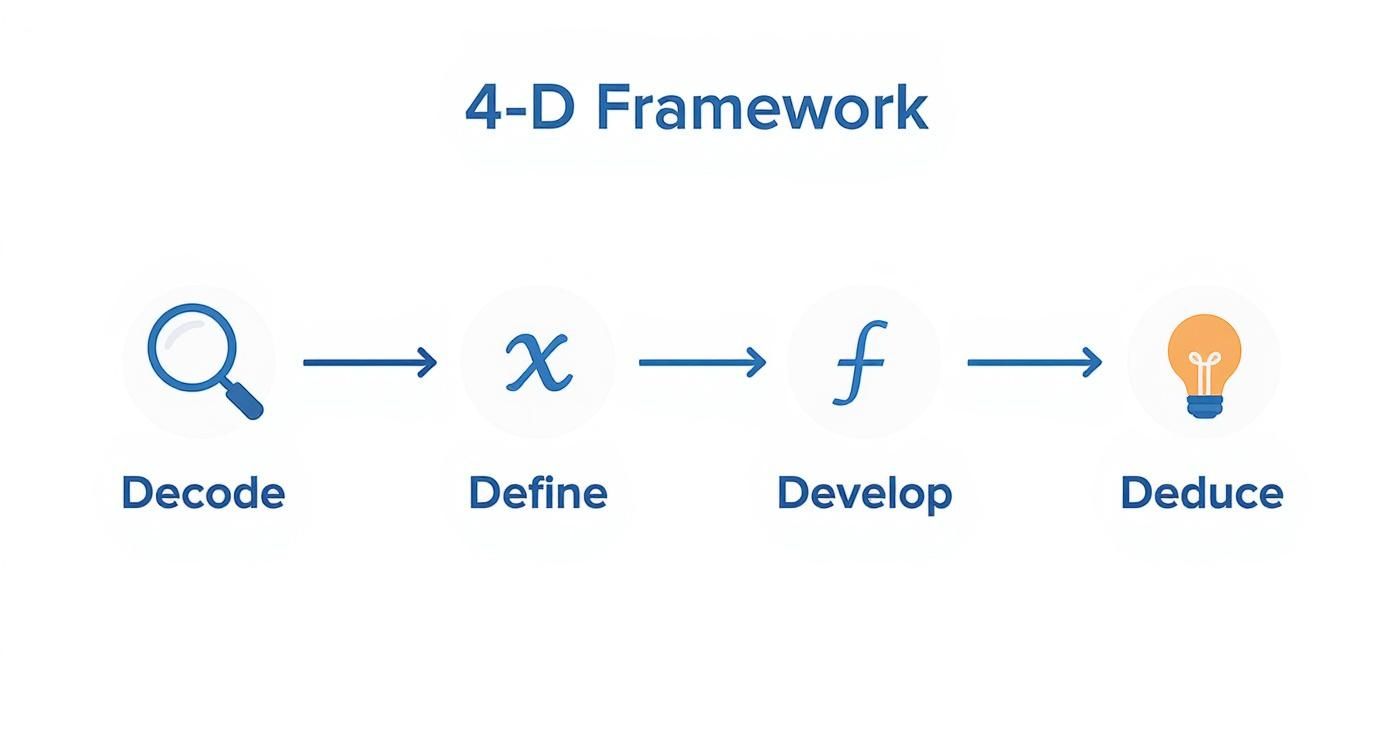
To make it even clearer, here is a quick summary of the strategy.

The 4-D Framework for Solving Word Problems

Phase	Objective	Key Action
Decode	Understand the story and the goal.	Read the problem multiple times. Identify knowns, unknowns, and the question.
Define	Assign a mathematical symbol to the unknown.	Choose a variable (like x) to represent the quantity you need to find.
Develop	Translate the words into an equation.	Write an algebraic equation that models the relationships in the problem.
Deduce	Find the solution and verify it.	Solve the equation and check if the answer is logical in the real-world context.

By consistently following these four steps, you create a reliable roadmap. You'll stop missing crucial details and can confidently move from text to solution every single time. It turns a big, scary task into a series of small, logical wins.

Turning Words Into Math Equations

Here’s where the real magic happens. The single most important skill in cracking algebra word problems is turning plain English into a clean mathematical equation. This is the heart of it all—the "Develop" phase of our framework—and honestly, it's where most people get tripped up.

The trick isn’t to memorize a giant list of keywords. It’s about learning to see the mathematical relationships hiding in the sentences themselves.

Think of it like learning a new language. You don’t just memorize words; you learn how they fit together to form ideas. We're doing the same thing here, but our new language is algebra.

From Words to Operations

The first step is to spot the words and phrases that signal specific math operations. While you don’t want to rely only on keywords, they are fantastic clues for figuring out the problem's structure.

For instance, the word "is" (along with its cousins "are," "was," and "will be") is one of the most powerful translators you'll find. In nearly every case, it simply means equals (=). The moment you see it, you’ve likely found the balancing point for your entire equation.

Similarly, the word "of" often points to multiplication (×), especially when you're working with percentages or fractions. If you see "50% of a number," your brain should immediately think 0.50 * x. Recognizing these patterns is the foundation for building the right equation.

My Favorite Tip: Read the problem out loud. Seriously. Hearing the words can help you identify the natural pauses and connections between different pieces of information, making it much easier to spot where the operations and the equals sign should go.

Assigning Variables That Actually Make Sense

Once you start seeing the operations, you need to handle the unknown—the number the problem is asking you to find. This is where you assign a variable. While 'x' is the classic go-to, I always tell my students to use letters that make more sense in the context of the problem.

If you’re asked to find the width of a rectangle, use 'w'. If it's about the distance a car traveled, try 'd'. This small adjustment is a game-changer for two big reasons:

• It keeps the abstract math grounded in the real-world story.
• When you finally solve for 'w = 10', you instantly know you've found the width, which helps you avoid mixing up your answers.

This little habit connects the abstract algebra back to the concrete problem you started with, which is a core part of learning how to solve word problems in algebra effectively.

A Practical Translation Guide

To help you get started, I've put together a quick reference table with some of the most common phrases you'll run into and what they mean in the language of algebra. Think of this as your starter phrasebook.

Common Word Problem Phrases and Their Algebraic Translations

Phrase or Keyword	Implied Operation	Example Sentence	Algebraic Expression
Sum, more than, increased by	Addition (+)	The sum of a number and 5 is 12.	x + 5 = 12
Difference, less than, minus	Subtraction (-)	A number decreased by 7 equals 10.	x - 7 = 10
Product of, times, twice	Multiplication (×)	The product of 4 and a number is 20.	4x = 20
Quotient of, divided by, ratio	Division (÷)	The quotient of a number and 3 is 9.	x / 3 = 9
Is, equals, results in	Equals (=)	Three more than a number is 15.	x + 3 = 15

Use this table to build your confidence. The more you practice, the more you’ll start to spot these patterns instantly, making the whole translation process feel less like a chore and more like a reflex. For more general advice, our guide on how to solve math problems step-by-step offers a broader look at developing strong problem-solving habits.

Remember, building the equation is often the toughest part. But once you master this translation skill, you turn a confusing story into a straightforward puzzle you already know how to solve.

Diving Into Different Types of Word Problems

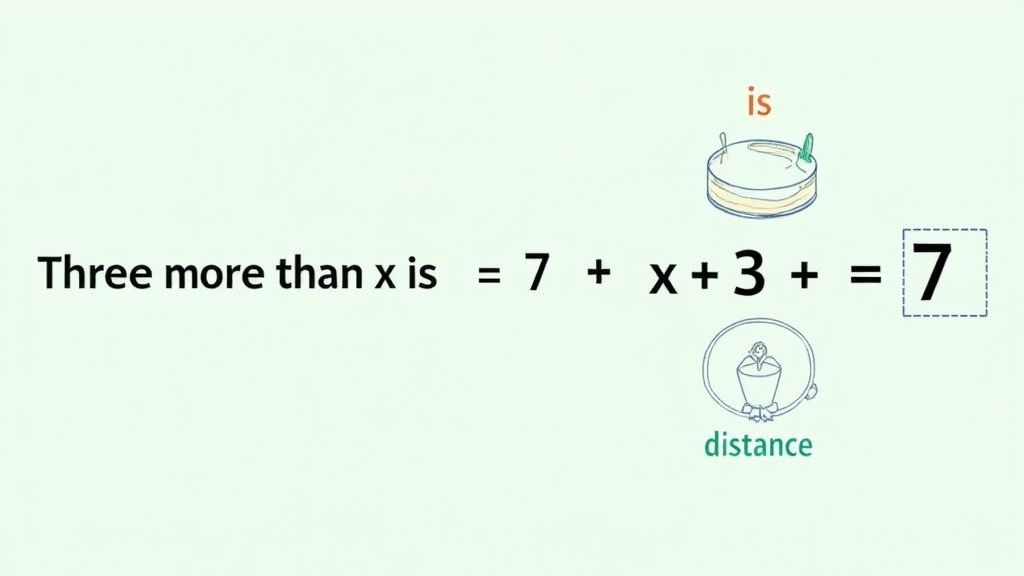
Alright, you've got the basic framework for turning words into math. Now comes the fun part: putting it to work. Different scenarios call for different setups, but that core process of decoding, defining, and developing the equation always holds true.

Think of each problem type as a unique puzzle with its own blueprint. Once you learn to spot the blueprint, everything clicks into place much faster. We'll walk through a few classic examples, from simple number puzzles to more involved problems about distance and shapes, using our 4-D method.

Getting Started with Number and Age Problems

Number and age problems are the perfect training ground. They're straightforward and let you focus entirely on the relationship between quantities, helping you build confidence in the translation process without a lot of extra fluff.

Let's break down a classic:

Problem: "A father is 30 years older than his son. In 12 years, the father will be twice as old as his son. How old is the son now?"

First, we decode the story. We've got two people, a father and a son. We know their current age difference and a specific relationship between their ages in the future. The goal is the son's current age.

Next, we define our variable. The question asks for the son's current age, so that’s our primary unknown.

• Let s = the son's current age.

Since the father is 30 years older, we can express his age using s:

• Father's current age = s + 30

Now we develop the equation based on the future. The problem jumps ahead "12 years," so let's figure out their ages then:

• Son's age in 12 years = s + 12
• Father's age in 12 years = (s + 30) + 12 = s + 42

The key phrase is "the father will be twice as old as his son." That's our equation:

• (Father's future age) = 2 * (Son's future age)
• s + 42 = 2(s + 12)

Finally, we deduce the answer by solving for s:

• s + 42 = 2s + 24
• 42 - 24 = 2s - s
• s = 18

The son is 18 years old. Let's double-check: If the son is 18, the father is 18 + 30 = 48. In 12 years, the son will be 30, and the father will be 60. Is 60 twice 30? Yes. Perfect.

Tackling Distance, Rate, and Time Problems

Distance, rate, and time problems are a staple of algebra for a reason—they model real-world motion. They all revolve around one core formula: Distance = Rate × Time (D=RT). The real trick is keeping all the information organized.

Here's a common scenario you'll see:

Problem: "Two trains leave stations 360 miles apart at the same time, traveling toward each other. One train travels at 80 mph, and the other travels at 70 mph. How long will it take for them to meet?"

Decode: We have two trains on a collision course. We know their speeds and the starting distance between them. We need to find the travel time.

Define: The unknown is how long they travel. Since they start and meet at the same time, their travel time (t) is the same.

• Let t = the time in hours until they meet.

Develop: Let's use D=RT to map out what's happening.

• Train 1: Rate = 80 mph, Time = t, Distance = 80t
• Train 2: Rate = 70 mph, Time = t, Distance = 70t

The lightbulb moment for this type of problem is realizing that when they meet, the distance Train 1 traveled plus the distance Train 2 traveled must add up to the original distance between them.

• (Distance of Train 1) + (Distance of Train 2) = Total Distance
• 80t + 70t = 360

Deduce: Now, just solve for t.

• 150t = 360
• t = 360 / 150
• t = 2.4 hours

A quick check confirms it. In 2.4 hours, Train 1 covers 80 × 2.4 = 192 miles, and Train 2 covers 70 × 2.4 = 168 miles. Add them up: 192 + 168 = 360 miles. It works.

Solving Geometry and Perimeter Problems

Geometry word problems are where algebra meets the physical world. They usually test your knowledge of formulas for perimeter, area, or volume. The key is to grab the right formula and then translate the problem's descriptions into relationships between the shape's dimensions.

Let's look at a typical perimeter problem:

Problem: "The length of a rectangle is 5 inches more than twice its width. If the perimeter is 70 inches, what are the dimensions of the rectangle?"

Decode: The problem is about a rectangle. We're given the total perimeter and a clear relationship between its length and width. The goal is to find the actual numbers for both.

Define: We have two unknowns, but they're connected. Since the length is described in terms of the width, let's start with w.

• Let w = the width of the rectangle.
• The length (l) is "5 more than twice its width," so l = 2w + 5.

Develop: We need the formula for a rectangle's perimeter: P = 2l + 2w. We can plug in everything we know: P is 70, and we have our expressions for l and w.

• 70 = 2(2w + 5) + 2w

Pro Tip: When a problem involves two unknowns, always look for the sentence that connects them. Defining one variable in terms of the other (like l = 2w + 5) is the secret to solving with a single equation.

Deduce: It's time to solve.

• 70 = 4w + 10 + 2w
• 70 = 6w + 10
• 60 = 6w
• w = 10 inches

With the width found, the length is easy:

• l = 2(10) + 5 = 20 + 5 = 25 inches

Let's check the perimeter: P = 2(25) + 2(10) = 50 + 20 = 70 inches. The dimensions fit perfectly.

As problems get more complex, you might run into scenarios with multiple distinct variables and equations. For those, understanding how to handle them simultaneously is crucial. If you see a problem with two unknowns and two separate relationship statements, our guide on how to solve systems of linear equations is the perfect next step.

Common Mistakes to Avoid

Even with a solid game plan, a few common slip-ups can derail your calculations in a heartbeat. Knowing how to solve word problems in algebra is just as much about knowing what not to do. This is your guide to the most frequent traps I've seen students fall into—and more importantly, how you can sidestep them for good.

Think of it like learning the rules of the road. Once you can spot the hazards ahead of time, you can navigate with a lot more confidence. Let's break down the most common pitfalls that trip up even the sharpest students.

Misinterpreting Subtraction Phrases

This one is sneaky, and it's probably the most common mistake of all. When a problem says "5 less than a number," our first instinct is to write 5 - x. It feels natural, but it's completely backward.

The correct way to write it is x - 5. Just think it through: if the number (x) were 10, "5 less than 10" is obviously 5. You only get that by calculating 10 - 5. So, always pinpoint the main quantity you're starting with, and then subtract from it.

Pro Tip: Whenever you see phrases like "less than" or "subtracted from," physically circle the number you're subtracting from. That term has to come first in your expression. This one simple habit can save you from a world of hurt.

Forgetting to Distribute a Negative Sign

The distributive property seems simple enough until a negative sign camps out in front of the parentheses. It is incredibly easy to distribute that negative to the first term and then completely forget about the second one.

• The Problem: Simplify 10 - (2x + 4)
• The Common Mistake: 10 - 2x + 4, which gives you the wrong answer of 14 - 2x.
• The Correct Way: 10 - 2x - 4, which simplifies to the right answer, 6 - 2x.

That little negative sign applies to every single term inside the parentheses. It's like multiplying each term by -1. Missing this will guarantee your answer is wrong, no matter how perfect the rest of your work is.

Mixing Up Your Units

Word problems love to test your attention to detail by mixing units. You might be given a speed in miles per hour but asked for a travel time in minutes. Or maybe a rectangle's length is in feet while its width is in inches.

If you don't convert everything to a consistent unit before you even start solving, your equation is broken from the start. For instance, if a car travels for 30 minutes at 60 miles per hour, you have to convert the time to 0.5 hours before plugging it into the D=RT formula.

Here’s a quick mental checklist to run through every time:

• Time: Is everything in seconds, minutes, or hours?
• Distance: Are we working with inches, feet, or miles?
• Money: Are we dealing with cents or dollars?

Make this unit check a non-negotiable part of your setup process.

The Most Critical Final Step You Should Never Skip

Finally, one of the biggest blunders is stopping too soon. You found a value for x, so you're done, right? Not so fast. The single most important final step is checking your answer against the original story, not just against your equation.

Why is this so crucial? Plugging your solution back into your own equation only confirms that you did the math correctly. It doesn't prove that your equation was the right one to begin with.

To do a real sanity check, take your final answer and see if it makes sense in the context of the actual problem.

• Does the age you calculated make sense? (A negative age is a huge red flag.)
• Does the distance you found align with the story's conditions?
• Do the dimensions you found actually produce the correct perimeter?

This last step is your safety net. It catches both simple calculation errors and, more importantly, those tricky initial translation mistakes. It’s what separates a good student from a great one.

Helpful Tools and Resources for Practice

Getting good at algebra word problems is a bit like learning to play guitar. You can’t just read about chords; you have to put in the hours and build up that muscle memory. The same goes for math. Working through problem after problem is what really cements the concepts, and thankfully, you've got more than just a textbook to help you out.

The right tools can make all the difference, turning frustrating practice sessions into focused, productive ones. There's a whole world of apps, websites, and even AI assistants out there that can give you the endless drills and instant feedback you need to build real confidence.

Online Practice Platforms and Mobile Apps

Forget just relying on the problems at the end of the chapter. The internet is packed with fantastic resources designed to sharpen your algebra skills. You can find websites with huge libraries of problems, often sorted by type—so you can hammer away at those tricky distance-rate-time questions until they finally click. Mobile apps are great, too, letting you squeeze in a quick study session while waiting for the bus.

Here are a few things I always recommend students look for:

• Step-by-Step Solvers: Find platforms that don't just spit out the final answer. The real value is in seeing the problem broken down, step-by-step. It helps you pinpoint exactly where you went off track.
• Gamified Apps: Let’s be honest, drills can be boring. Apps that turn math into a game with points and challenges can be a surprisingly effective way to stay motivated.
• Concept Refreshers: Sometimes the problem isn't the word problem itself, but a shaky understanding of a core algebra concept. A good website with clear, simple explainers on things like factoring or linear equations can be a lifesaver.

Expert Tip: The goal isn't just getting the answer right. It's about mastering the process so it becomes automatic. Use these tools to practice the routine: read, define variables, write the equation, and solve. Repetition is key.

Using AI to Study Smarter

AI is changing the game for students. Think of it as having a personal tutor on call 24/7. These tools are perfect for getting you unstuck on a tough problem or creating a custom-made practice session. If you're curious about the bigger picture, it's worth reading about AI's role in enhancing education to see how these technologies are being used.

This screenshot shows how an AI tool can break down a complex algebra concept into simple, understandable parts.

Notice how it provides not just a definition but a worked-out example. That’s what makes an abstract idea concrete.

An AI math solver like the one at https://feen.ai/ai-math-solver can give you a line-by-line breakdown for any problem you're stuck on, showing you exactly where you made a mistake. But it goes beyond that. You can ask it to generate 10 more practice problems just like the one you're struggling with, or even ask it to rephrase a confusing question in a simpler way. That kind of personalized help makes it much easier to push past those frustrating learning plateaus on your own.

Frequently Asked Questions

Even with a solid game plan, you're bound to run into a few tricky spots. That’s completely normal. Let’s tackle some of the most common questions that pop up when you're wrestling with algebra word problems.

What Is the Most Important Step?

Hands down, the most crucial part of the entire process is translating the story into the right algebraic equation. It's so tempting to rush this part and jump straight into solving, but that's where most mistakes happen. If your setup is wrong, even perfect calculations won't save you.

My advice? Live in the "Develop" phase for a bit longer than feels necessary. Read the problem two or three times. Really nail down what you're being asked to find and how all the pieces of the puzzle relate to each other. Getting the equation right is more than half the battle.

Key Takeaway: Slowing down at the start actually speeds you up. An extra minute spent double-checking your equation will save you from ten minutes of backtracking and frustration. A solid setup makes the rest of the work a breeze.

How Can I Get Better at Recognizing Problem Types?

Pattern recognition is a skill, and like any skill, it gets better with practice. The more word problems you do, the more you'll start to see the familiar skeletons underneath the stories. For instance, if you read about cars, trains, or planes, your brain should immediately think Distance = Rate × Time. See different solutions being poured together? That’s almost certainly a mixture problem.

To get there faster, I highly recommend creating a personal "cheat sheet." On one page, write down the fundamental formulas for the common problem types you see in your homework:

• Rate Problems: D = RT
• Mixture Problems: (Amount 1)(Value 1) + (Amount 2)(Value 2) = (Total Amount)(Final Value)
• Consecutive Integer Problems: x, x + 1, x + 2...
• Simple Interest Problems: I = PRT

Keep this sheet handy while you work. Glancing at it will help you categorize problems on the fly and build the mental reflexes you'll need on a test.

What if My Answer Does Not Make Sense?

First off, don't panic! Getting a weird answer—like a negative length or 2.5 people—is actually a good thing. It's a flashing red light telling you to stop and check your work. It's an invaluable opportunity to find and fix a mistake.

Usually, the issue lies in one of two places. The most common culprit is a mistake in the initial equation. Maybe you misinterpreted a phrase like "less than" or just put a plus sign where a minus sign should have been. Go back to the original problem and compare it, word for word, with the equation you wrote.

If the setup looks solid, the second place to check is your algebra. It's surprisingly easy to make a small arithmetic error or forget to distribute a negative sign all the way through a parenthesis. This is exactly why checking your work at the end isn't just a suggestion; it’s a non-negotiable step to catch these logical errors and make sure your answer holds up.

---

Feeling stuck on a particular problem or just want more targeted practice? Feen AI can give you a hand. Snap a photo of any word problem, and our AI homework helper will break it down with a clear, step-by-step explanation. Get the guidance you need to understand the process by visiting the Feen AI website.