Mastering mass to moles conversion: Quick Steps & Real Examples

To convert a substance's mass to moles, you just need to do one simple thing: divide its mass (in grams) by its molar mass (in grams per mole). This straightforward calculation is one of the most crucial skills you'll learn in chemistry. It's the bridge connecting the stuff you can physically weigh on a scale to the invisible world of atoms and molecules. Master this, and you've unlocked the key to stoichiometry and truly understanding chemical reactions.

Why Converting Mass to Moles Is a Fundamental Chemistry Skill

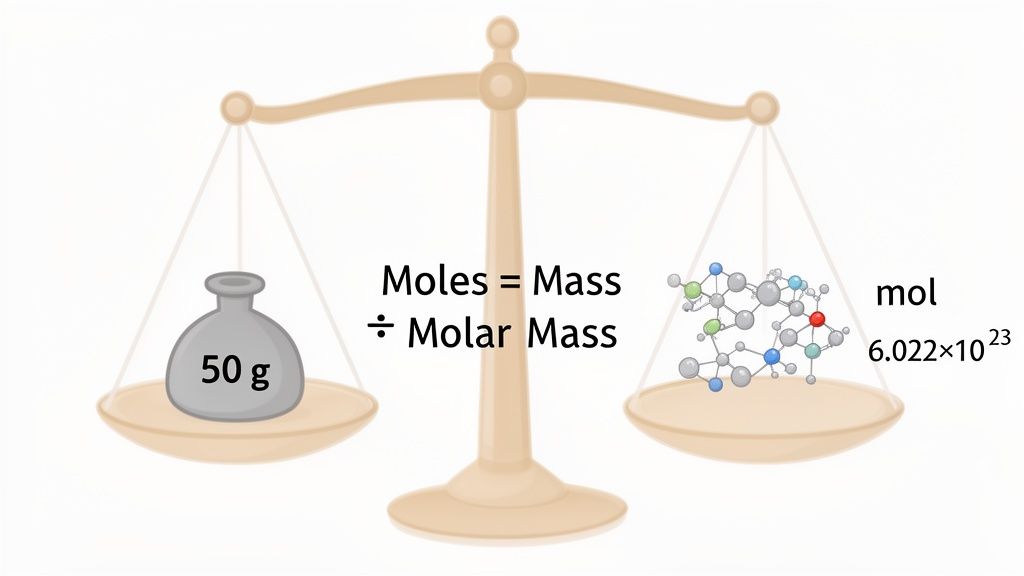
Think about it this way: what if a cake recipe told you to add 1.8 x 10²⁵ molecules of flour and 8.8 x 10²⁴ molecules of sugar? It would be impossible. You can't sit there and count out trillions upon trillions of molecules, but you can easily weigh out a few hundred grams.

Chemists face this exact dilemma. The mass-to-moles conversion is their solution. It lets them work with tangible, measurable amounts while knowing exactly how many particles are reacting on a microscopic level.

At its core, the mole is just a unit for counting, like how a "dozen" means 12. A mole, however, represents a mind-bogglingly huge number: 6.022 x 10²³ particles. This value, known as Avogadro's number, is the standard that links the atomic scale with our everyday macroscopic world.

The Role of Molar Mass

To make that leap from mass to moles, you need a unique conversion factor: molar mass. The molar mass is simply the mass of one mole of a substance, always expressed in grams per mole (g/mol). It’s a distinct value for every element and compound, and you find it by using the atomic masses on the periodic table.

It’s like comparing a dozen feathers to a dozen bowling balls. Both have 12 items, right? But their weights are drastically different. The same logic applies here. One mole of helium and one mole of gold both contain the same number of atoms (6.022 x 10²³), but their masses aren't even close.

• Helium (He): Its molar mass is about 4.00 g/mol.
• Gold (Au): Its molar mass is about 197.0 g/mol.

This means if you measure out 4 grams of helium, you're holding exactly one mole of helium atoms. If you have 197 grams of gold, you've got one mole of gold atoms. Molar mass is the specific key that makes the conversion possible for any substance you can think of.

Before we jump into the formula itself, here’s a quick reference table to keep the key terms straight. It’s a good idea to get comfortable with these definitions, as they are the building blocks for all these calculations.

Quick Guide to the Mass to Moles Formula

Term	Definition	Example
Mass (g)	The amount of a substance, measured in grams.	50 g of water (H₂O).
Moles (mol)	The unit for an amount of substance, equal to 6.022 x 10²³ particles.	2.78 mol of water.
Molar Mass (g/mol)	The mass of one mole of a substance, found using the periodic table.	Molar mass of H₂O is ~18.02 g/mol.

This table neatly summarizes everything you need. The formula simply connects these three concepts, allowing you to find any one value if you know the other two.

The History Behind the Mole

The whole idea of linking mass to a set number of particles didn't just appear overnight. It started with a concept from Italian chemist Amedeo Avogadro way back in 1811. He proposed that equal volumes of different gases, under the same conditions, contain an equal number of particles.

His work laid the essential groundwork for mass-to-mole conversions, even though the scientific community didn't really accept it for another 50 years. The first real estimate of this massive number came in 1865, and it was finally named 'Avogadro's number' in 1908 by French physicist Jean Perrin to honor the man whose ideas were so central to modern chemistry. For a deeper dive, you can read more about the history of the mole and see how it developed over nearly a century.

Key Takeaway: The mole is how chemists "count" atoms by weighing them. The formula—mass divided by molar mass—is the tool that makes this translation happen, turning a simple measurement from a lab scale into powerful chemical information.

Getting this skill down isn't just about acing a test; it's about learning to speak the language of chemistry. It's used every single day in fields ranging from pharmaceutical development to materials science and environmental testing. Every chemical reaction, from the simplest one in a high school lab to the complex synthesis of a new drug, depends on getting the mole ratios exactly right. Your journey into the quantitative side of chemistry starts here.

Getting to Grips with Molar Mass

Before you can tackle any mass to moles conversion, you need one crucial piece of the puzzle: the molar mass. Think of it as the specific "grams-to-moles" exchange rate for any substance. It's measured in grams per mole (g/mol), and the good news is you don't have to memorize a thing. Everything you need is laid out for you on the periodic table.

The periodic table is so much more than a colorful grid. For a chemist, it’s a toolkit, and one of its most important tools is the atomic mass listed for each element. This number, usually found right below the element’s symbol, is the average mass of a single atom in atomic mass units (amu). But here’s the magic: that same number also represents the mass of one mole of those atoms in grams.

Take carbon (C), for example. Its atomic mass is about 12.011 amu. This also means that one mole of carbon atoms weighs 12.011 grams. Just like that, you have its molar mass: 12.011 g/mol.

How to Read the Periodic Table for Atomic Mass

When you glance at the periodic table, you'll see a few numbers in each element's box. It's vital to grab the right one for your calculation.

The number you're after is the atomic mass—almost always the one with decimal places. You’ll want to be careful not to mix it up with the atomic number, which is always a whole number (like 2 for Helium) and tells you the number of protons. For any mass to moles conversion, the atomic mass is your target.

From Single Elements to Full Compounds

Finding the molar mass for a single element is as simple as reading it off the chart. But what about compounds, which are the bread and butter of chemistry? It's just as straightforward—you just need to add up the parts.

To find the molar mass of any compound, you simply sum the atomic masses of every single atom in its chemical formula.

Let's break down the method you can use every single time, whether you're working with table salt or something far more complex.

• List the Elements: First, identify every element in the chemical formula. For sulfuric acid (H₂SO₄), you have Hydrogen (H), Sulfur (S), and Oxygen (O).
• Count the Atoms: Next, check the subscripts (the small numbers) to see how many atoms of each element are present. In H₂SO₄, we have 2 hydrogen atoms, 1 sulfur atom, and 4 oxygen atoms.
• Add It All Up: Finally, multiply the atom count for each element by its atomic mass from the periodic table, then sum the results.

A Quick Tip From Experience: Don't round the atomic masses from the periodic table too much. For most lab work or homework problems, keeping at least two decimal places will keep your final answer accurate and prevent rounding errors.

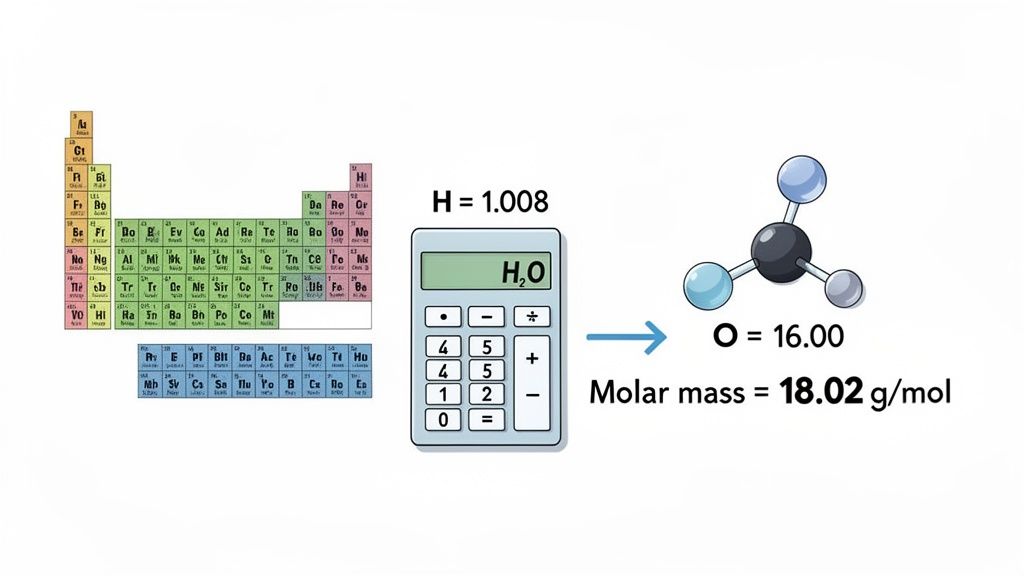
Let’s Walk Through an Example: Water (H₂O)

Let's put this into practice with a compound everyone knows: water (H₂O).

1. Identify and Count: The formula H₂O tells us we have 2 atoms of Hydrogen (H) and 1 atom of Oxygen (O).
2. Look Up Atomic Masses: A quick check of the periodic table shows Hydrogen's atomic mass is roughly 1.01 g/mol, and Oxygen's is 16.00 g/mol.
3. Do the Math:
   • Hydrogen: 2 atoms × 1.01 g/mol = 2.02 g/mol
   • Oxygen: 1 atom × 16.00 g/mol = 16.00 g/mol
   • Total Molar Mass = 2.02 + 16.00 = 18.02 g/mol

The molar mass of water is 18.02 g/mol. This is your conversion key—it means that 18.02 grams of water is equal to exactly one mole of H₂O molecules. Now you’re ready to plug this value into your mass to moles conversion.

Mastering this skill is fundamental. If you want more practice, check out our complete guide on how to calculate molar mass. Getting this down will make all your future chemistry calculations feel like second nature.

A Practical Walkthrough Of The Conversion Process

Okay, now that you have a feel for what molar mass is, let's put it to work and perform a full mass to moles conversion. This is where the rubber meets the road. The whole process really just comes down to one simple formula: dividing the mass of your substance by its molar mass.

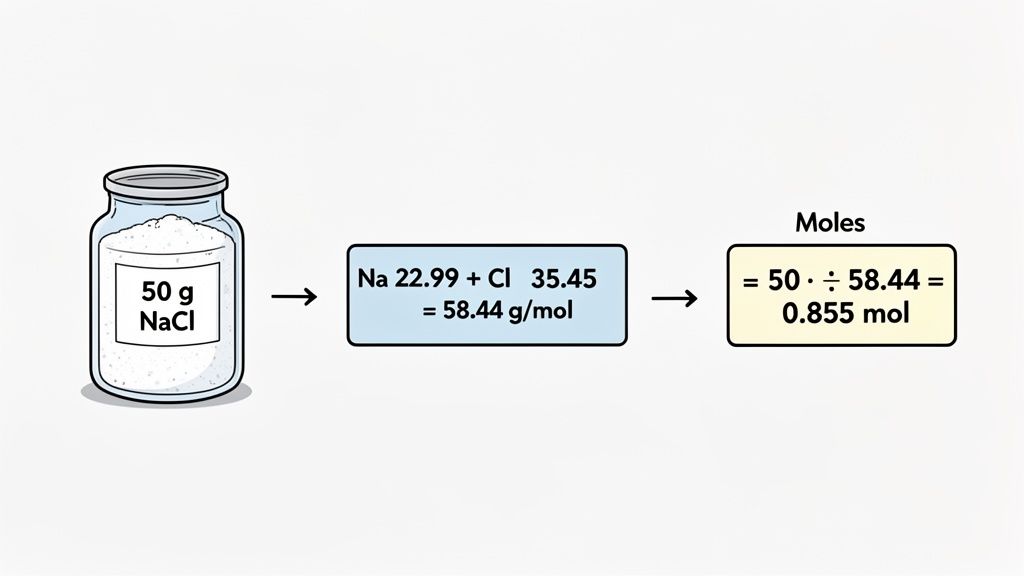
Let's ground this in a real-world scenario. Imagine you're in the lab (or even your kitchen) and you weigh out 50 grams of sodium chloride (NaCl)—that's just regular table salt. How many moles of salt do you actually have? This is the exact calculation chemists run all day to make solutions and figure out reaction quantities.

The formula you'll keep coming back to is the key to everything:

Moles = Mass (in grams) / Molar Mass (in g/mol)

This little equation is your bridge from something you can physically measure on a scale (mass) to the specific number of particles you're dealing with (moles). It’s the most direct way to get from "how much does it weigh?" to "how many do I have?"

Your Action Plan For Conversion

Let’s stick with our 50 grams of NaCl and walk through the calculation together. This isn't just about punching numbers into a calculator; it’s about understanding why you're doing each step.

First, figure out what you already know. The problem hands you the mass on a silver platter: 50 g of NaCl. The other piece of the puzzle you need is the molar mass of sodium chloride.

Time to pull out the periodic table.

• The atomic mass of Sodium (Na) is about 22.99 g/mol.
• The atomic mass of Chlorine (Cl) is about 35.45 g/mol.

Add them together, and you get the molar mass for NaCl: 22.99 + 35.45 = 58.44 g/mol.

Perfect. Now you have both parts you need: the mass (50 g) and the molar mass (58.44 g/mol). You're ready to do the actual mass to moles conversion.

Applying The Formula

Let's plug our numbers into the formula and see what we get.

• Mass: 50 g
• Molar Mass: 58.44 g/mol

Moles of NaCl = 50 g / 58.44 g/mol

Run that calculation, and you end up with approximately 0.8556 moles of NaCl.

Take a second to look at the units. The grams (g) on the top (from mass) and the bottom (from molar mass) cancel each other out, leaving you with "moles." This is a fantastic little trick to confirm you've set up your problem correctly.

So, what does this number mean? It means that in those 50 grams of table salt, you're holding about 0.86 moles of NaCl. In chemistry, that number is far more useful than the mass alone, especially when you need to predict how it will react with something else. The best part? This exact process works for any substance, from pure iron to complex molecules. It's a fundamental skill you'll use constantly, especially when you learn how to balance chemical equations, since those reactions are based on mole ratios.

Let's run through a few more examples to really lock this in.

Worked Examples Of Mass to Moles Conversions

The best way to get comfortable with the mass to moles conversion is to just do it a few times. This table shows the process for a few different compounds, but you'll see the core steps are always the same.

Compound	Given Mass (g)	Molar Mass (g/mol)	Calculation (Mass / Molar Mass)	Result (moles)
Water (H₂O)	100 g	18.02 g/mol	100 g / 18.02 g/mol	5.55 mol
Glucose (C₆H₁₂O₆)	25 g	180.16 g/mol	25 g / 180.16 g/mol	0.139 mol
Iron (Fe)	75 g	55.85 g/mol	75 g / 55.85 g/mol	1.34 mol
Carbon Dioxide (CO₂)	10 g	44.01 g/mol	10 g / 44.01 g/mol	0.227 mol

Each row follows the exact same logic: grab the mass, find the molar mass, and then divide. This systematic approach will give you the right answer every time, no matter how intimidating the chemical formula might look. It’s a repeatable skill that serves as the foundation for almost everything else in chemistry.

How to Avoid Common Conversion Mistakes

You've got the formula down and the periodic table in front of you. The mass to moles conversion should be straightforward, right? But as anyone who's spent time in a lab knows, a tiny slip-up can send your answer way off track. It happens to everyone, but learning to spot the common pitfalls is the fastest way to build real accuracy and confidence.

These aren't complicated conceptual errors; they're the small, easy-to-make stumbles that can derail an entire calculation. Think of this as your pre-flight check, helping you spot potential turbulence before you even take off. Let’s walk through the most frequent tripwires I've seen over the years and how to sidestep them for good.

Mistaking Atomic Number for Atomic Mass

This is, without a doubt, the most common mistake I see, especially with students who are just starting out. The periodic table throws a few numbers at you for each element, and it's incredibly easy to grab the wrong one in a hurry.

Remember, the atomic number—that big, bold whole number, usually at the top—is the element's identity. It tells you the number of protons, but it has nothing to do with its mass. What you're looking for is the atomic mass, which is almost always a decimal value found right below the element's symbol.

• Wrong: Using 8 for Oxygen (O). That's its atomic number.
• Correct: Using 16.00 g/mol for Oxygen (O), its atomic mass.

Make it a habit to always glance below the symbol for that decimal number. This one simple check will save you from countless molar mass miscalculations.

Forgetting to Account for Subscripts

In a chemical formula, those little numbers hanging off the element symbols—the subscripts—are everything. They tell you exactly how many atoms of that element are in a single molecule. Forgetting to multiply by the subscript is a classic error when adding up the molar mass.

Take water (H₂O). It’s so tempting to just add hydrogen's mass to oxygen's mass and move on. But that little "2" in H₂O is telling you there are two hydrogen atoms to account for.

The Common Error: Calculating H₂O molar mass as 1.01 (for H) + 16.00 (for O) = 17.01 g/mol.

The Right Way: You have to multiply the hydrogen mass by its subscript first: (2 × 1.01 g/mol) + 16.00 g/mol = 18.02 g/mol. That's a pretty significant difference, and it will completely change your final answer.

Always scan the formula for subscripts before you even touch your calculator. It's a quick, two-second step that guarantees your molar mass is right from the start.

The Problem with Diatomic Elements

Here's a sneaky one. Some elements, in their natural state, don't like to be alone. They pair up into molecules. These are the seven diatomic elements, and they can catch you off guard if a problem refers to them by name, like "oxygen gas" or "liquid nitrogen."

These are the seven you need to commit to memory:

• Hydrogen (H₂)
• Nitrogen (N₂)
• Oxygen (O₂)
• Fluorine (F₂)
• Chlorine (Cl₂)
• Bromine (Br₂)
• Iodine (I₂)

So, if a problem asks you to find the moles in 32 grams of oxygen gas, it’s talking about O₂, not a single oxygen atom (O). Your molar mass calculation has to reflect that reality.

• Incorrect Molar Mass: 16.00 g/mol (for a single O atom).
• Correct Molar Mass: 2 × 16.00 g/mol = 32.00 g/mol (for an O₂ molecule).

Using the wrong molar mass here would literally cut your final answer in half. Always pay close attention to how the substance is described—it’s a major clue.

Ignoring Unit Consistency

The standard mass to moles conversion is built on a simple foundation of units: mass needs to be in grams (g) and molar mass in grams per mole (g/mol). But sometimes, a problem will throw you a curveball by giving you the mass in kilograms (kg) or milligrams (mg) just to test your attention to detail.

If you're given 2.5 kg of a substance, you can't just plug "2.5" into the formula. That's a guaranteed path to the wrong answer.

Let's see it in action. You need to find the moles in 2.5 kg of table salt (NaCl), which has a molar mass of 58.44 g/mol.

1. First, Convert Your Units: Convert kilograms to grams. Since 1 kg = 1000 g, then 2.5 kg becomes 2500 g.
2. Now, Do the Real Calculation: Moles = 2500 g / 58.44 g/mol ≈ 42.78 mol.

If you had skipped that first step, your calculation would have been 2.5 / 58.44 = 0.0428 mol—a wildly different and incorrect result. Always, always check your units before you divide. It's the bedrock of a correct calculation.

Practice Problems to Build Your Confidence

Watching someone work through a problem is a good start, but the real learning happens when you roll up your sleeves and try it yourself. This is where the concept clicks. The best way to get comfortable with the mass to moles conversion is to tackle a few challenges head-on.

I’ve put together a few problems here that are designed to build your skills progressively. We'll start with a simple, single element, then move on to a common compound, and finally, tackle a problem that throws a little unit conversion into the mix. This way, you can make sure you've mastered one step before adding another layer of complexity.

Take your time with each one. Seriously, write out your steps, show your work, and double-check those molar mass calculations. The goal here isn’t speed—it’s about understanding the why behind the calculation.

Problem 1: A Simple Start with Iron

Let's begin with a straightforward element. Think of this as a warm-up to make sure you're comfortable with the basic formula and pulling numbers from the periodic table.

• Question: How many moles are in 25.0 grams of pure iron (Fe)?

Solution:

1. Identify Given Mass: The problem gives us 25.0 g.
2. Find Molar Mass: A quick look at the periodic table for iron (Fe) tells us its molar mass is 55.85 g/mol.
3. Apply the Formula: Moles = Mass / Molar Mass
4. Calculate: Moles = 25.0 g / 55.85 g/mol ≈ 0.448 moles of Fe.

This first problem is a direct plug-and-play. You have the mass, you find the molar mass—it's just a simple division problem to get your answer.

Problem 2: A Common Compound

Alright, let's try a problem with a compound. This adds the crucial pre-step of calculating the molar mass before you can actually do the conversion.

• Question: Calculate the number of moles in 150 grams of calcium carbonate (CaCO₃), the main stuff in chalk and limestone.

Solution:

1. Identify Given Mass: We have 150 g.
2. Calculate Molar Mass of CaCO₃:
   • Calcium (Ca): 1 × 40.08 g/mol = 40.08 g/mol
   • Carbon (C): 1 × 12.01 g/mol = 12.01 g/mol
   • Oxygen (O): 3 × 16.00 g/mol = 48.00 g/mol
   • Total Molar Mass = 40.08 + 12.01 + 48.00 = 100.09 g/mol.
3. Apply the Formula: Moles = 150 g / 100.09 g/mol
4. Calculate: Moles ≈ 1.50 moles of CaCO₃.

This example really highlights how important it is to get that molar mass calculation right. You have to account for every single atom in the chemical formula. If you want more practice with these types of calculations, our guide on stoichiometry practice problems with answers is a great next step.

Problem 3: A Unit Conversion Challenge

Let’s add a realistic twist. In the lab or in industry, you're not always going to be working with grams. This problem tests your ability to spot and handle different units before you dive into the main calculation.

• Question: You have a 0.50 kg bag of glucose (C₆H₁₂O₆). How many moles of glucose does it contain?

Solution:

1. Convert Units First: The mass is in kilograms, but our molar mass is in grams per mole. We need them to match.
   • 0.50 kg × (1000 g / 1 kg) = 500 g.
2. Calculate Molar Mass of C₆H₁₂O₆:
   • Carbon (C): 6 × 12.01 g/mol = 72.06 g/mol
   • Hydrogen (H): 12 × 1.01 g/mol = 12.12 g/mol
   • Oxygen (O): 6 × 16.00 g/mol = 96.00 g/mol
   • Total Molar Mass = 72.06 + 12.12 + 96.00 = 180.18 g/mol.
3. Apply the Formula: Moles = 500 g / 180.18 g/mol
4. Calculate: Moles ≈ 2.77 moles of C₆H₁₂O₆.

Key Takeaway: Always, always, always check your units before you start plugging numbers into the formula. A quick conversion at the beginning is the key to avoiding a massive error in your final answer. The mass-to-moles formula only works when the units are consistent.

By working through these problems, you've practiced the core skill and handled the most common curveballs you're likely to see. Keep at it, and this fundamental chemistry calculation will become second nature.

Frequently Asked Questions About Moles and Mass

Even after you've mastered the steps, a few questions always seem to come up about how mass, moles, and chemical equations all fit together. Getting these sorted out will really solidify your understanding and save you headaches later on. Let’s dig into some of the most common ones that pop up when you're doing a mass to moles conversion.

Why Can’t I Just Use Grams in Chemical Equations?

This is a great question because it cuts right to the core of why the mole concept is so important. At their heart, chemical reactions are about atoms and molecules bumping into each other and rearranging. The problem is, different atoms have wildly different weights. A single atom of lead, for instance, is way heavier than a single atom of hydrogen.

Because of this, one gram of lead contains drastically fewer atoms than one gram of hydrogen.

Using grams in an equation would be like trying to bake a cake using a recipe that calls for "one cup of eggs." It just doesn't work. Moles, on the other hand, standardize the number of particles. One mole of lead has the exact same number of atoms (6.022 x 10²³) as one mole of hydrogen. This allows chemists to mix and match reactants with total precision.

Think of moles as chemistry's universal translator for "how many." They let us compare the number of particles involved in a reaction, not just their weight.

What Is the Difference Between Molar Mass and Molecular Weight?

You'll often hear these two terms used as if they're the same thing, and for practical purposes, they almost are. But there's a small, key difference in what they're actually describing.

• Molecular Weight: This is the mass of just one individual molecule, measured in a tiny unit called atomic mass units (amu). It’s a term for the microscopic world.
• Molar Mass: This is the mass of an entire mole of that substance—a full 6.022 x 10²³ particles. It's the lab-scale number you'll see on the periodic table, measured in grams per mole (g/mol).

The numbers themselves are identical. A single water molecule has a molecular weight of around 18 amu, and the molar mass of water is 18 g/mol. When you're tackling a mass to moles conversion problem, molar mass is the value you'll be using every time.

How Do I Convert from Moles Back to Mass?

Going in the other direction—from moles back to grams—is just as common and, thankfully, just as straightforward. All it takes is a quick flip of the formula we’ve been using.

We started with the equation Moles = Mass / Molar Mass. With a bit of simple algebra, we can rearrange it to solve for mass instead.

The formula becomes:

Mass (g) = Moles × Molar Mass (g/mol)

To make the conversion, you'll still need the molar mass from the periodic table. Just multiply that number by the moles you have, and the answer will be the mass of your sample in grams.

---

Stuck on a tricky chemistry problem or need a step-by-step explanation for a tough assignment? Let Feen AI be your go-to homework helper. Just upload a picture of your problem, and get clear, concise solutions and explanations for Chemistry, Physics, Math, and more. Try it now at https://feen.ai and make studying simpler.