How To Solve System Of Equations Using Elimination

When you're faced with a system of equations, the elimination method is a powerful algebraic tool. At its heart, it's about adding or subtracting the equations to make one of the variables disappear. This clever move simplifies the problem, letting you solve for one variable and then work backward to find the other.

It's a fantastic alternative to graphing or substitution, especially when you spot coefficients that are opposites or easily made into opposites.

Why the Elimination Method Works So Well

So, why can we just add two equations together? Think of each equation as a perfectly balanced scale. If you add or subtract the same amount from both sides, it stays balanced. The elimination method is just an extension of that logic—you're combining two balanced scales to create a new one that's also balanced, just simpler.

This technique is particularly slick when your equations are already lined up in standard form (Ax + By = C). It turns a tricky two-variable puzzle into a simple one-variable equation that’s much easier to crack.

Comparing Elimination to Other Methods

While graphing is a great way to visualize the solution, it’s not always precise enough. Substitution works well, but it can get bogged down in messy fractions if you can't easily isolate a variable.

Elimination, however, is a direct algebraic attack. It keeps the calculations clean, especially when none of the variables have a convenient coefficient of 1 or -1. In those situations, elimination is often the most efficient path forward. For a full breakdown of different strategies, check out our guide on how to solve systems of linear equations.

A Method with Deep Roots

This idea of eliminating variables has a long and fascinating history. We often call it Gaussian elimination after the 19th-century mathematician Carl Friedrich Gauss, who used it for complex astronomical calculations. But the core concept is much older.

Incredibly, Chinese mathematicians described a very similar method in a text dating back to around 200 BCE. It’s a testament to the power and elegance of the idea.

Key Takeaway: The whole point of elimination is to simplify. By strategically combining equations, you knock one variable out of the park, making the entire system much easier to solve.

Grasping this core principle is the first step. It's what will help you master this method, whether you're in a classroom or tackling real-world problems like analyzing circuits in an engineering lab.

Putting Elimination to Work: A 2x2 System

Alright, let's get our hands dirty with a classic 2x2 system of equations. Theory is great, but seeing the elimination method in action is where it really clicks. We'll walk through an example where the variables don't just cancel out on their own—a common situation you'll run into.

Here’s the system we're going to tackle:

• 3x + 2y = 7
• 5x - 4y = 8

First thing's first: look at the setup. Both equations are already in the standard Ax + By = C format, and all the like terms are lined up vertically. This kind of organization is your best friend; it helps you sidestep simple mistakes right from the start.

Choosing Your Target: Which Variable to Eliminate?

So, do we go after x or y? Let's size up the coefficients. For the x-terms, we have a 3 and a 5. To get them to cancel, we’d have to find their least common multiple, which is 15. That means multiplying the top equation by 5 and the bottom one by 3. Totally doable, but it's a bit of work.

Now, look at the y-terms: 2 and -4. This looks much more promising. I can turn that 2y into a 4y with just one multiplication. Even better, the signs are already opposite (+2y and -4y), so they're perfectly primed to cancel each other out when we add the equations. Let’s make y our target.

To get the y-coefficients to be opposites, all we need to do is multiply the entire first equation by 2. Remember, you have to multiply every single term in the equation to keep everything balanced.

• 2 * (3x + 2y = 7) gives us 6x + 4y = 14

Let's slot this new, modified equation back into our system:

1. 6x + 4y = 14
2. 5x - 4y = 8

See that? The +4y and -4y are now ready to be eliminated.

Combining the Equations and Solving for X

With our equations lined up, we can just add them together, column by column. This is where the magic happens—the y-terms vanish, leaving us with a simple, one-variable equation.

(6x + 5x) + (4y - 4y) = (14 + 8)
11x + 0 = 22
11x = 22

From here, solving for x is a breeze. Just divide both sides by 11.

x = 22 / 11
x = 2

We've got half the answer! Finding the first variable is a huge step, but we're not quite done. Now we need to find the value of y that goes with it.

A Quick Tip from Experience: When you substitute your first variable back in, always pick the simplest of the original equations. It just reduces the chances of making a small arithmetic error. For us, 3x + 2y = 7 looks a little easier to work with.

Let's plug x = 2 into that equation:

3(2) + 2y = 7
6 + 2y = 7

Subtract 6 from both sides:

2y = 1

And finally, divide by 2:

y = 1/2 (or 0.5, if you prefer decimals)

So, our solution is the coordinate pair (2, 0.5). It’s always a good habit to quickly check your answer by plugging both values into the other original equation (5x - 4y = 8) to make sure it all holds together.

Solving 3x3 Systems With Elimination

Jumping from two variables to three can feel like a big step up in complexity, but the core logic of the elimination method stays exactly the same. The goal is to systematically whittle that 3x3 system down into a more familiar 2x2 system.

Think of it like breaking a big project into smaller, more manageable tasks. You’ll pick one variable to eliminate and get rid of it twice, using different pairs of equations. This process leaves you with two brand-new equations that only contain the other two variables.

The Two-Stage Elimination Process

Let's say you're looking at a system with variables x, y, and z. The first thing you need to do is decide which variable to get rid of first. Take a quick scan of the coefficients—are any of them opposites already? Or are any of them easy multiples of each other? That's your target.

Here’s the general game plan:

1. First Pass: Pick two equations and combine them to eliminate your chosen variable (let's say it's 'z').
2. Second Pass: Now, pick a different pair of equations and eliminate that exact same variable ('z') again.
3. Solve the New System: You're left with two new equations that form a simple 2x2 system. From here, you just solve for the remaining two variables like we did before.

This infographic breaks down the fundamental steps you'll be applying at each stage of the process.

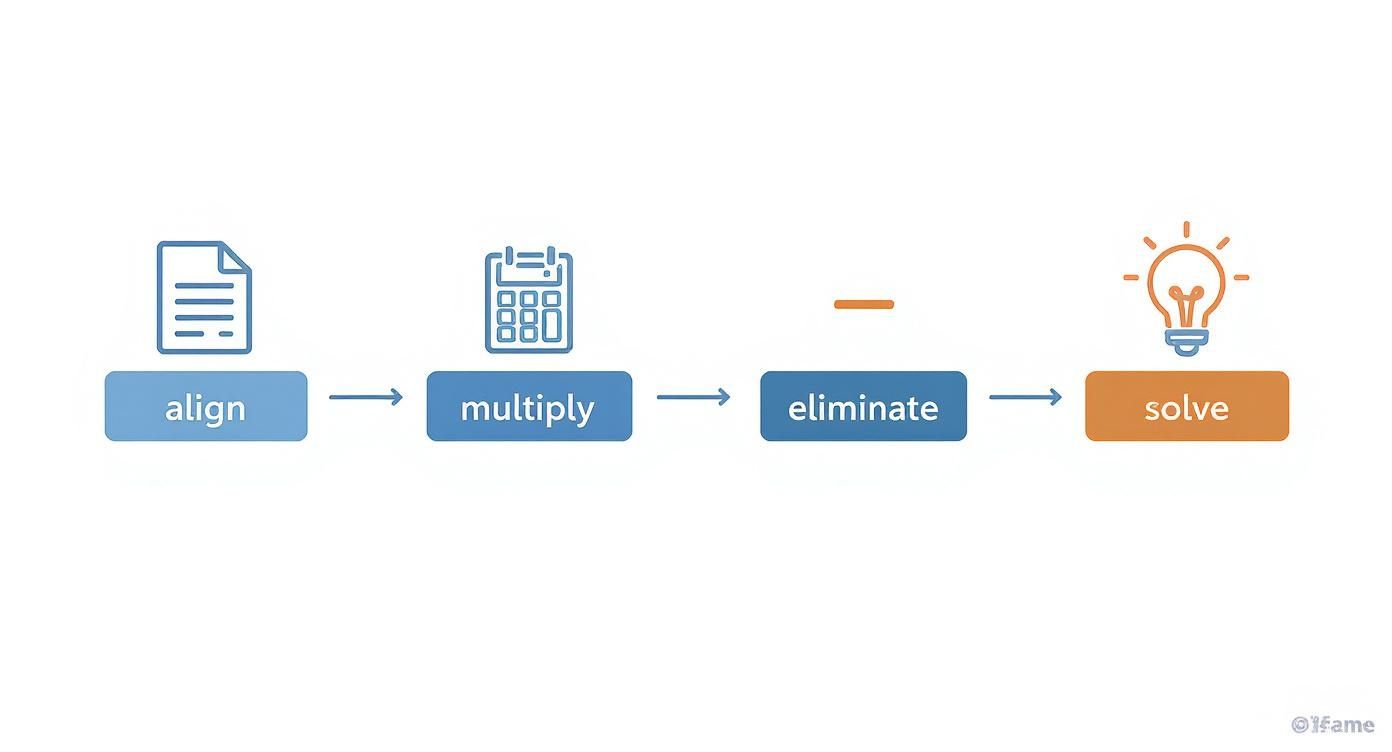
The visual nails the core cycle: align, multiply, eliminate, and solve. You’ll just repeat that a couple of times to crack the 3x3 puzzle.

Working Through a 3x3 Example

Let's get our hands dirty with a real example. Take a look at this system:

• (A) x + y + z = 6
• (B) 2x - y + z = 3
• (C) x + 2y - 3z = -4

Glancing at the coefficients, I immediately see that the y-terms in equations (A) and (B) are +y and -y. They're already perfect opposites. This makes 'y' a fantastic first variable to eliminate.

First Elimination
We can just add equations (A) and (B) together directly:

(x + y + z) + (2x - y + z) = 6 + 3
3x + 2z = 9 (Let's call this Equation D)

Second Elimination
Now, we have to eliminate 'y' again, but this time using a different pair. Let's use (B) and (C). To make the y-terms cancel, we'll need to multiply equation (B) by 2.

2 * (2x - y + z = 3) → 4x - 2y + 2z = 6

Now, we add this modified equation to equation (C):

(4x - 2y + 2z) + (x + 2y - 3z) = 6 + (-4)
5x - z = 2 (And this is our new Equation E)

Pro Tip: Organization is your best friend here. Seriously. Labeling your original equations (A, B, C) and your new ones (D, E) makes it so much easier to track your work and avoids those frustrating "where did this number come from?" moments.

Solving the Reduced System and Back-Substituting

We've successfully boiled our big problem down to a simple 2x2 system using our new equations, D and E:

• (D) 3x + 2z = 9
• (E) 5x - z = 2

Let's finish this by eliminating 'z'. If we multiply equation (E) by 2, the z-terms will be opposites.

2 * (5x - z = 2) → 10x - 2z = 4

Add that to equation (D):

(3x + 2z) + (10x - 2z) = 9 + 4
13x = 13
x = 1

We've got our first variable! Now we just work our way back up. Plug x=1 into an easy equation from our 2x2 system—equation (E) looks good:

5(1) - z = 2
5 - z = 2
z = 3

Almost there. We take x=1 and z=3 and plug them into one of the original equations. Equation (A) is definitely the simplest:

1 + y + 3 = 6
4 + y = 6
y = 2

And there we have it. The final solution is (1, 2, 3).

While elimination is a powerful hands-on method, you'll find that for much more complex systems, especially in fields like engineering and computer science, these problems are often tackled using matrices. If you're curious, you can learn more about how to solve matrix equations in our detailed guide.

Method Comparison for Solving Linear Systems

Choosing the right tool for the job makes all the difference. Here’s a quick breakdown of when to use substitution, elimination, or graphing.

Method	Best For	Key Challenge
Substitution	When one equation is already solved for a variable (e.g., y = 2x - 1).	Can lead to messy fractions if no variable is easily isolated.
Elimination	When coefficients are opposites or easy multiples. Great for standard form (Ax + By = C).	Requires careful multiplication to make coefficients match.
Graphing	Visualizing the solution and identifying no-solution or infinite-solution cases.	Not precise for non-integer solutions; can be time-consuming to draw accurately.

Each method has its moment to shine. Getting comfortable with all three gives you the flexibility to solve any system efficiently.

Dealing with No Solution and Infinite Solutions

Most of the time, when you solve a system of equations, you get a clean answer—a single (x, y) point where the lines cross. But every so often, the math takes an unexpected turn. The elimination method is brilliant at exposing these special cases: systems with either no solution or infinitely many solutions.

This isn't just a quirky math problem; it has real-world meaning. For an economist, it might mean supply and demand curves never meet at a feasible price. For an engineer, it could signal two design constraints that are impossible to satisfy at the same time.

When You Have No Solution

You know you've hit this scenario when you follow all the steps for elimination, and suddenly, both variables vanish. You’re left with an equation that makes no sense.

Here’s a textbook example:

• 2x + 3y = 5
• -2x - 3y = -8

When you add these two equations together, the x terms cancel out, and so do the y terms. All you're left with is:

0 = -3

This is a contradiction. We know that zero does not equal negative three. When your algebra leads you to a patently false statement like this, it’s a red flag. It’s the system's way of telling you there is no solution. Graphically, this means you're dealing with two parallel lines that will never, ever cross.

When You Have Infinite Solutions

On the flip side, what happens when the variables disappear and you're left with a statement that is undeniably true? This is the sign of infinite solutions.

Take a look at this system:

• x - 2y = 4
• -3x + 6y = -12

First, let's multiply the top equation by 3 to set up the elimination:

3(x - 2y = 4) → 3x - 6y = 12

Now, let's add our newly modified equation to the original second equation:

(3x - 6y) + (-3x + 6y) = 12 + (-12)

Everything on the left cancels out, and so does everything on the right. The result?

0 = 0

This statement, while not giving us a specific answer, is always true. It indicates that both of the original equations are actually describing the exact same line. They’re just dressed up differently. Since every point on the line satisfies both equations, there are infinitely many solutions.

Key Takeaway: A false statement (like 0 = -3) means no solution. A true statement (like 0 = 0) means infinite solutions. These aren't errors; they are the definitive answers for these unique systems.

Learning to spot these outcomes is a core skill. The elimination method is a cornerstone of algebra curriculum for a reason—it’s taught in 87% of secondary schools in a survey across 30 countries. In the United States, over 10 million students encounter this method each year, especially when prepping for standardized tests like the SAT and ACT. You can dive deeper into its applications by exploring the systems of equations by elimination chapter in more detail.

Common Mistakes and How to Avoid Them

Even with the steps memorized, it's surprisingly easy to make a small error that throws off the entire solution. Learning how to solve system of equations using elimination is just as much about dodging common pitfalls as it is about knowing the process. A single misplaced negative sign or a multiplication mistake can send you down a rabbit hole.

The number one mistake I see is forgetting to multiply the entire equation. If you decide to multiply an equation by 3 to get your coefficients to match, you have to multiply the x-term, the y-term, and the constant on the other side. It’s an easy detail to miss, but skipping even one term unbalances the whole equation and makes a correct answer impossible.

Another classic trip-up is a simple sign error, especially when subtracting one equation from another. This is particularly common when you're subtracting an equation that has negative terms. Remember, subtracting a negative is the same as adding a positive. It's a tiny detail that's easy to overlook when you're focused on the bigger picture.

Staying Accurate and Organized

The best way to sidestep these issues is to be methodical. Keeping your work neat isn't just about appearances—it's one of the best tools you have for maintaining accuracy.

• Don't skip steps: It's tempting to do the multiplication and addition in your head, but don't. Write down the newly modified equations before you try to combine them.
• Leave yourself breadcrumbs: If you multiply the first equation by -2, jot down a quick note like (R1) * -2 in the margin. This makes it a thousand times easier to retrace your steps and find a mistake.
• Do a quick sign check: Right before you add or subtract, take a second to confirm that the coefficients you're targeting are actually opposites (like +4y and -4y).

My golden rule? The final check is non-negotiable. Always, always plug your final (x, y) or (x, y, z) solution back into all of the original equations. If it only works for one, you know you've gone wrong somewhere.

Building Good Habits Through Practice

Getting comfortable with elimination just takes practice. To make sure you're getting the most out of your time, it helps to incorporate effective Maths GCSE revision strategies into your study sessions. The more you practice, the more the steps become second nature, letting you work both faster and more accurately.

If you're looking for a wider view on mathematical problem-solving, our guide on how to solve math problems step by step provides some great frameworks that can help with far more than just systems of equations.

Got Questions? Let's Clear Things Up

Once you get the hang of the elimination method, you start to see the patterns. But even so, a few common questions tend to trip people up. Let's tackle those head-on so you can solve these problems with more confidence and speed.

Think of this as the inside scoop—the little tips and tricks that make the whole process smoother.

Which Variable Should I Get Rid of First?

This is probably the number one question I get. The simple answer? Go for the easiest target. You want to choose the path of least resistance.

Before you do anything else, just take a second to scan the coefficients for all your variables (x, y, and z).

• Look for perfect opposites. See a +5x in one equation and a -5x in another? That's your golden ticket. They're already set up to cancel out when you add the equations together. No extra work needed.
• Find the simple multiples. What if you have a 3y and a 6y? That's also a great starting point. It only takes one quick multiplication to turn that 3y into a -6y.

The goal is efficiency. Picking the easiest variable to eliminate not only saves you time but also seriously cuts down on the chances of making a small calculation mistake.

What Do I Do if My Equations Have Fractions?

Fractions can look intimidating, but they're easy to deal with. The trick is to get them out of the way before you start the elimination process. Don't even try to work with them.

For each equation, find the least common denominator (LCD) of any fractions present and multiply the entire equation by that number.

Let’s say you have something like (1/4)x - (1/2)y = 3. The LCD here is 4. Just multiply everything by 4:

4 * [(1/4)x - (1/2)y = 3] → x - 2y = 12

Look at that—no more fractions. Now you have a clean, simple equation that's much easier to work with.

My Advice: Seriously, always clear out the fractions first. It feels like an extra step, but it makes the rest of the problem so much simpler and less error-prone. It's a game-changer.

Is Elimination Always the Best Method?

For most problems where the equations are already lined up in standard form (Ax + By = C), elimination is a powerhouse. It's clean, organized, and incredibly efficient.

In fact, this method is so effective that a more advanced version of it, called Gaussian elimination, is a cornerstone of scientific computing. When scientists and engineers need to solve massive systems with many variables, this is the method they turn to.

Just how fast is it? A 2018 study on computational efficiency found that for a system with 7 variables, Gaussian elimination solved it in a blistering 46 milliseconds. A similar technique, Gauss-Jordan elimination, took 76 milliseconds to get the same job done. You can see the full breakdown in this research paper on solving linear equations.

So, is it always the fastest? Not necessarily. If you have an equation where one variable is already isolated (like y = 3x + 5), the substitution method is probably going to get you to the answer a little quicker. It’s all about choosing the right tool for the job.

---

Still wrestling with a tricky problem or just want to double-check your work? Feen AI can help you out. Snap a picture of your homework, and our AI tutor will walk you through the steps for Math, Chemistry, Physics, and more. It’s a great way to stop guessing and start learning. Get instant homework help with Feen AI.