how to solve a system of equations: A Practical Guide

When you're faced with a system of equations, the goal is pretty straightforward: find the one set of values for all the variables that makes every single equation true. Think of it as finding the single point where multiple lines or curves cross paths.

The most common tools in our toolbox for this are substitution, elimination, and graphing. Each has its own strengths, and knowing which one to grab for a specific problem is half the battle. Once you get the hang of these, you'll be able to pinpoint that unique coordinate pair where everything lines up.

Understanding the Basics of Equation Systems

At its heart, a "system" is nothing more than a collection of two or more equations that are all connected by the same variables. It’s like a puzzle. You’re hunting for a set of numbers that magically works in every equation at the same time. This "solution" is the specific coordinate pair, usually (x, y), that satisfies the entire system.

This isn't just a random algebra exercise, either. It’s the hidden machinery behind a ton of real-world scenarios.

• Business and Economics: Businesses use systems to find their break-even point—that sweet spot where total cost equals total revenue.
• Engineering: From designing a bridge to analyzing an electrical circuit, engineers are constantly solving systems to ensure things work safely and efficiently.
• Navigation: The GPS in your phone is a master at this. It solves a complex system of equations, using signals from multiple satellites to figure out your precise location on the globe.

Possible Outcomes You Can Expect

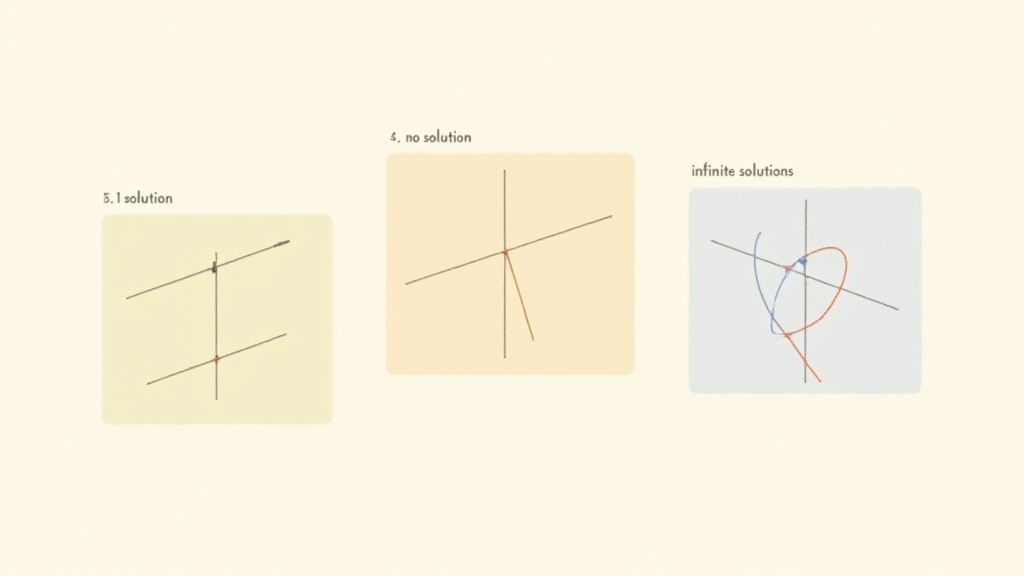
When you dive into solving a system, you're going to land on one of three possible outcomes. Knowing what these are ahead of time helps you make sense of the answer you get.

Most of the time, you'll find one unique solution. This is the classic case where the graphs of your equations intersect at a single, distinct point.

Sometimes, though, you'll discover there's no solution at all. This happens when you have parallel lines—they run alongside each other forever but never cross. Algebraically, your work will dead-end into a contradiction, something obviously false like 0 = 5.

The third possibility is that you have infinitely many solutions. This occurs when your equations are actually just two different ways of describing the exact same line. In this case, every single point on that line is a valid solution.

A Glimpse into the Past

The challenge of solving these kinds of problems isn't new; it's ancient. The earliest known methods trace back almost 4,000 years to Babylonian mathematicians, who used them to solve practical problems in trade and astronomy.

Over the centuries, these techniques were sharpened by cultures around the world, from ancient China to 18th-century Europe, where mathematicians like Gabriel Cramer made huge leaps. This long history just goes to show how fundamental this skill really is.

If you're ready to get started, our guide on how to solve math problems step-by-step is a great place to begin.

Using the Substitution Method

The substitution method is one of the most reliable algebraic tools in your arsenal for solving a system of equations. The whole idea is pretty clever: solve one equation for a single variable, and then substitute that expression into the other equation. This move instantly transforms a tricky two-variable problem into a much more manageable single-variable one.

This strategy is your best friend when you see a variable that's either already by itself or can be easily isolated. If you glance at a system and one equation is already in a y = ... or x = ... format, that's a big flashing sign that substitution will be the most direct route to the answer.

Isolating a Variable and Making the Swap

Let's get our hands dirty. The first move is to pick one equation and get a variable alone on one side of the equals sign.

Take this system, for example:

2x + y = 11 x - 3y = -9

That x in the second equation is practically begging to be isolated. Since it has no coefficient, the algebra is clean and simple. Just add 3y to both sides, and you get x = 3y - 9. Easy.

Now for the "substitution" part. You're going to plug this new expression for x into the other equation—the one you haven't touched yet. This is absolutely crucial. If you substitute it back into the same equation you started with, you'll just end up going in circles.

We'll replace x in 2x + y = 11 with our new expression, (3y - 9):

2(3y - 9) + y = 11

Just like that, x is gone. We're left with a single equation that only involves y. Now we're on familiar ground.

Solving for the First Variable

With our new, simpler equation, it's time to solve for y. This usually involves some basic algebra: distributing, combining like terms, and getting the variable by itself.

Let's pick up where we left off with 2(3y - 9) + y = 11.

• First, distribute the 2: 6y - 18 + y = 11
• Next, combine the y terms: 7y - 18 = 11
• Now, add 18 to both sides: 7y = 29
• Finally, divide by 7: y = 29/7

Boom. We've got the value for our first variable. That's a huge step, but remember, the solution to a system needs a value for both x and y.

Pro Tip: Be incredibly careful with your signs when distributing. A common trip-up is forgetting to carry a negative sign through to every term inside the parentheses. A quick double-check here can save you a ton of frustration later on.

Finding the Second Variable and Verifying

The final step is what's known as back-substitution. We simply take the value we just found (y = 29/7) and plug it back into one of the original equations to find x. The easiest path is often using that rearranged equation we made at the very beginning: x = 3y - 9.

Let's plug in our value for y:

x = 3(29/7) - 9 x = 87/7 - 63/7 x = 24/7

And there we have it—our complete solution is (24/7, 29/7). This is the exact coordinate where the two lines from our original equations cross paths.

To be 100% sure, always check your answer. Plug both x and y values into the other original equation (2x + y = 11) to make sure everything holds true.

2(24/7) + 29/7 = 11 48/7 + 29/7 = 11 77/7 = 11 11 = 11

It checks out perfectly. This final verification is your safety net, catching any small arithmetic slips you might have made along the way.

Sometimes, substitution can lead to more complex situations. For instance, plugging a linear equation into a quadratic one might leave you needing to solve a quadratic equation. If you find yourself in that spot, our guide on how to factor polynomials completely is a great resource to have on hand.

Solving with the Elimination Method

When you run into a system of equations where all the variables are neatly lined up, the elimination method is often your best bet. This technique really shines when equations are in the standard Ax + By = C form, because it’s designed to make one of the variables simply disappear.

The whole point is to add or subtract the equations from each other to cancel out either the x or y term. This leaves you with a single, straightforward equation with just one variable, which is a breeze to solve.

Aligning and Eliminating a Variable

The real magic of elimination happens when the coefficients of one variable are opposites. Think +3y in one equation and -3y in the other. When you add the equations, they’re perfectly set up to cancel each other out.

Take a look at this system:

• 2x + 3y = 7
• 4x - 3y = 5

Here, the y terms are practically begging to be eliminated. By adding the two equations together, the +3y and -3y sum to zero, knocking y out of the picture.

2x + 4x = 6x 3y + (-3y) = 0 7 + 5 = 12

The entire system simplifies down to one easy equation: 6x = 12. A quick division gives you x = 2.

When You Need to Adjust the Equations

Of course, problems aren't always set up so perfectly. More often than not, you'll need to multiply one or even both equations by a constant to create those matching opposite coefficients. This is where the real strategy comes in.

Let's work with a new system:

• 3x + 2y = 8
• x + 5y = 7

Right now, nothing cancels. But we can easily manipulate the second equation to make the x terms opposites. All we have to do is multiply the entire second equation by -3.

-3(x + 5y) = -3(7) -3x - 15y = -21

Now, our modified system looks like this:

• 3x + 2y = 8
• -3x - 15y = -21

The x terms are ready to go. Adding them together gives us -13y = -13, which simplifies beautifully to y = 1.

Key Takeaway: The goal is to find the least common multiple of the coefficients for whichever variable you want to eliminate. This keeps the numbers you're working with as simple as possible and helps cut down on calculation mistakes.

Handling Special Cases: No Solution or Infinite Solutions

Every so often, using the elimination method leads to a weird result where both variables vanish. Don't panic! This isn't a mistake—it's an important clue about the relationship between the two equations.

• No Solution: If both variables disappear and you're left with a false statement (like 0 = 10), it means the lines are parallel and will never intersect. The system has no solution.
• Infinite Solutions: If the variables disappear and you end up with a true statement (like 0 = 0), it tells you that both equations are just different ways of describing the exact same line. The system has infinitely many solutions.

Finalizing and Checking Your Solution

Once you've solved for one variable, you’re on the home stretch. The last step is the same as in the substitution method: back-substitution. Just plug the value you found back into one of the original equations to find the other variable.

In our last example, we found y = 1. Let's plug that into the simpler original equation, x + 5y = 7:

x + 5(1) = 7 x + 5 = 7 x = 2

So, our solution is the point (2, 1). It's always a good idea to double-check your work by plugging both values into the other original equation (3x + 2y = 8) to make sure it holds true.

3(2) + 2(1) = 8 6 + 2 = 8 8 = 8

It checks out. The elimination method is a fundamental skill, and it’s a stepping stone to more advanced techniques. If you're curious about how these ideas apply to larger systems, our guide on how to solve matrix equations is a great next step, as it builds on these very same principles.

Finding Solutions with the Graphing Method

While algebraic methods like substitution and elimination give you perfectly exact answers, there's something to be said for seeing the problem. That's where graphing comes in. It's a fantastic visual approach that turns abstract equations into lines on a coordinate plane, often making the solution feel instantly obvious.

The whole concept boils down to one simple idea: the solution to a system is the point where the graphs of the equations cross. Think about it—each line represents every possible (x, y) pair that satisfies its own equation. So, the one place they intersect has to be the single point that makes both equations true at the same time.

Plotting Your Way to a Solution

The easiest way to graph a linear equation is usually by getting it into slope-intercept form, which you'll remember as y = mx + b. This format is great because it tells you exactly what you need to draw the line.

• The y-intercept (b): This is your starting block. It’s the spot where the line crosses the vertical y-axis.
• The slope (m): This is the line's direction and steepness. The classic way to think of it is "rise over run"—how many units you move up (or down) for every unit you move to the right.

Let's say you're working with y = 2x - 1. You'd start by putting a dot on the y-axis at (0, -1). From that spot, the slope of 2 (which is the same as 2/1) tells you what to do next: go up 2 units and then right 1 unit. That lands you at (1, 1). Just connect those two points, and you've got your line.

A Quick Tip from Experience: Drawing graphs by hand is an incredible way to build your mathematical intuition. But when you need real precision, don't hesitate to use a digital tool. They take the human error out of the equation and let you see the answer in seconds.

Take a look at this screenshot from the Desmos graphing calculator. It shows a more complex system with a line (y = x + 1) and a parabola (y = x² - 2x - 3).

Instantly, you can see that these two graphs intersect at two separate points: (-1, 0) and (4, 5). Those are the two solutions for this nonlinear system, no algebra required to find them.

The Good and Bad of Graphing

The number one advantage of graphing is how clear it is. You get an immediate visual answer about what kind of solution you're looking at.

• One Solution: The lines cross at exactly one point. Simple.
• No Solution: The lines are parallel. They'll never intersect.
• Infinite Solutions: Both equations produce the exact same line, so they're on top of each other everywhere.

But graphing has one major drawback: it's not always precise. If your lines cross at a nice, neat point like (2, 5), it's easy to see. But if the true intersection is somewhere like (24/7, 29/7), you'd just be guessing. It's almost impossible to find that exact fractional answer just by looking at a graph you drew yourself.

Because of this, graphing is best used as a specific tool in your kit. It's perfect for getting a quick estimate, understanding what's happening in the system, or doing a quick "sanity check" on an answer you found algebraically. When you absolutely need the exact answer, you'll want to fall back on the rock-solid precision of substitution or elimination.

How to Choose the Right Method

Knowing the different ways to solve a system of equations is half the battle. The other half—and what really separates the pros from the novices—is knowing which method to use for a specific problem.

Making the right choice upfront can mean the difference between finding a solution in two minutes flat or spending ten minutes wrestling with messy fractions. The trick is to let the equations themselves tell you the easiest way forward.

Look for an Easy "In" with Substitution

Before you start crunching numbers, take a good look at the system. Do you see a variable that's already by itself, or one that would be incredibly easy to isolate?

If you spot an equation like y = 2x - 1 or an x with a coefficient of 1 or -1, that's a huge green light for the substitution method. It’s tailor-made for these situations. You can just grab that expression and plug it right into the other equation, no fuss, no extra steps.

When Elimination Is Your Best Bet

What if both equations are already lined up in standard form (Ax + By = C)? When you see the x-terms, y-terms, and constants all stacked neatly, your brain should immediately think elimination.

This setup is perfect for adding or subtracting the two equations to make one of the variables vanish. It's especially fast if you notice the coefficients for one variable are already the same or, even better, opposites (like 5x and -5x).

The Power of a Visual Check with Graphing

And what about graphing? While it's not always the best for getting a precise answer (unless you have a graphing calculator), it’s fantastic for understanding the big picture.

If you just need a quick estimate or want to see if there's one solution, no solution, or infinite solutions, graphing gives you that instant visual confirmation. It's the best way to see if the lines cross, run parallel, or are actually the same line.

This infographic sums up the decision-making process nicely.

Ultimately, the structure of the equations gives you all the clues you need.

Which Method Should I Use?

Here’s a quick reference table to help you decide on the fly. Looking at the "Situation" column and matching it to your problem will point you toward the most efficient path.

Situation	Best Method	Why It Works Best
One variable is already isolated (e.g., y = 3x + 5).	Substitution	It's the most direct route. No setup required—just plug it in.
Both equations are in standard form (Ax + By = C).	Elimination	The terms are already aligned, making it easy to add/subtract.
One variable has a coefficient of 1 or -1.	Substitution	It's simple to isolate that variable without creating fractions.
Coefficients of one variable are opposites (e.g., 2x and -2x).	Elimination	One quick addition and a variable is gone.
You need a visual understanding or a quick estimate.	Graphing	Instantly shows you the relationship between the lines.
You suspect there's no solution or infinite solutions.	Graphing	Parallel or identical lines are immediately obvious on a graph.

Think of this table as your cheat sheet. With a little practice, this choice will become second nature, and you'll find yourself solving systems much more quickly and confidently.

The goal isn't just to get the right answer, but to get it using the cleanest, most logical approach. Taking a few seconds to strategize first will save you a ton of time and potential headaches down the road. This is the kind of thinking that takes your math skills to the next level.

Where Math Meets the Real World

https://www.youtube.com/embed/NwOYLV-L7pc

It's easy to think of solving systems of equations as just another abstract math problem. But the skills you’re building here are the same ones that power some of the most important decisions and innovations all around us. This is the point where algebra leaves the textbook and starts explaining how the world actually works.

Take economics, for example. Experts use these systems to pinpoint market equilibrium—that sweet spot where the amount of a product people want to buy (demand) lines up perfectly with the amount companies are willing to sell (supply). That intersection point? It's the solution to their system. In the same way, electrical engineers use systems of equations to figure out current and voltage in complex circuits.

What Happens When Problems Get Bigger?

The methods we've walked through are fantastic for systems with two variables. But what about when things get more complicated? Many real-world challenges involve three, four, or even hundreds of variables. Think about a logistics company planning delivery routes across dozens of cities—that's a massive system of equations in action.

For these bigger challenges, we need a bigger toolkit.

• Systems with Three Variables: When you add a third variable, say z, you're no longer looking for where two lines cross on a flat plane. You're actually finding the single point in 3D space where three flat planes intersect. The core ideas of substitution and elimination still work, but the process has a few more layers.
• Matrices: Trying to solve huge systems by hand is a non-starter. This is where matrices come in. They offer a powerful, organized way to handle complex systems using methods like Gaussian elimination. They’re the engine behind the software used in everything from data science and machine learning to physics and engineering.

The 20th century completely changed how we tackle these large-scale problems. The rise of computers in the 1950s made it possible to use iterative methods like the Jacobi and Gauss-Seidel methods, which are now critical for scientific simulations. Today, you'll find that over 90% of STEM programs teach matrix-based solutions because they are so fundamental. For a deeper dive, check out the history of solving linear systems.

What This Means for You: Getting comfortable with two-variable systems is your foundation. Understanding that these same principles scale up with tools like matrices is what opens the door to tackling much more significant, real-world problems.

A Glimpse into the World of Curves

So far, we’ve stuck to linear equations—the ones that give us nice, straight lines. But the world isn't always so straightforward. Nonlinear systems are where you'll find equations that graph as circles, parabolas, and all sorts of other curves.

Imagine you need to figure out where a straight highway will intersect a circular park. That's a classic linear-quadratic system. Unlike the single solution we often see with lines, these systems can have one, two, or even more solutions, each one representing a point where the graphs touch or cross. Tackling these usually involves a blend of substitution and factoring, building directly on the skills you’ve already mastered. This is the next exciting step in your problem-solving journey.

Common Questions Answered

As you get more practice solving systems of equations, you'll inevitably run into a few weird situations. Sometimes the variables disappear completely, or the answers look messy. Let's walk through what these scenarios mean so you can solve any problem with confidence.

What if I Get a Nonsensical Answer Like 0 = 5?

Ever been in the middle of a problem, meticulously using substitution or elimination, only to end up with a statement that makes no sense, like 0 = 5 or -3 = 12? It’s a classic head-scratcher, but it’s not a mistake. It's actually a clue.

When your variables completely cancel out and leave you with a false statement, the system is telling you that the lines are parallel. Since parallel lines never cross, there is no solution.

And What if Everything Cancels Out to 0 = 0?

On the flip side, you might eliminate a variable and watch as everything disappears, leaving you with a true statement like 0 = 0 or 7 = 7.

This result means your two equations are describing the exact same line—they're just dressed up differently. Since the lines are identical, they overlap at every single point. This means there are infinitely many solutions.

A little pro tip: You can often spot this before you even start. If you notice one equation is just a multiple of the other (like x + y = 2 and 2x + 2y = 4), you're dealing with the same line.

Can I Mix and Match Methods?

Absolutely! In fact, the most experienced problem-solvers do this all the time. Blending techniques is often the smartest way to tackle more complex systems, especially those with three or more variables.

You could, for example, use elimination on the first two equations to get rid of the z variable. Then, take that new equation and use substitution with the third original equation. Don't feel like you have to stick with one method all the way through.

Does it Matter if My Answers Are Fractions or Decimals?

Not one bit. We get used to seeing nice, neat integer answers like (2, 3) in textbooks, but real-world problems are rarely so tidy. Getting fractions or decimals is completely normal.

An answer like (24/7, 29/7) is just as valid as (4, 5). The real test is whether it works. As long as you plug your values back into the original equations and they check out, you can be confident in your solution.

---

Feeling stuck on a tough problem or just need to check your work? The Feen AI homework helper can give you the clear, step-by-step explanations you need to master any concept. Upload a photo of your assignment and get unstuck in minutes at https://feen.ai.