Quadratic Formula Practice Problems Mastery(quadratic formula practice problems)

The quadratic formula, x = [-b ± √(b² - 4ac)] / 2a, is a fundamental tool in algebra, providing a reliable method for solving any quadratic equation. It’s the key to unlocking problems in fields ranging from physics and engineering to economics and finance. However, simply memorizing the formula isn't enough. True mastery comes from applying it confidently and accurately across a diverse set of challenges, each with its own unique twist.

This guide is designed to build that confidence. We have compiled a comprehensive list of quadratic formula practice problems that will take you from the basics to more advanced applications. You won't just find answers here; you'll find a strategic breakdown for each problem. We will guide you through identifying coefficients, calculating the discriminant, and interpreting the final solution, whether it's a clean integer, an irrational number, or a complex pair.

Our goal is to move you beyond rote memorization to genuine understanding. Each example is a mini-lesson in strategy, highlighting common pitfalls and offering actionable takeaways you can apply to future problems. We’ll cover everything from equations with fractional coefficients and complex solutions to real-world word problems that require you to set up the equation yourself. To truly master these concepts and prepare for assessments, exploring effective study methods is crucial. Many students find success by applying proven tips & strategies for Maths GCSE to structure their learning and retention. By working through these carefully selected problems, you will develop the skills needed to tackle any quadratic equation with precision and ease.

1. Basic Quadratic Formula Problem - Standard Form ax² + bx + c = 0

Every journey into algebra requires a solid first step, and for quadratic equations, that step is mastering the standard form: ax² + bx + c = 0. This is the foundational problem type where you directly apply the quadratic formula without any preliminary algebraic manipulation. It’s designed to build your confidence and ensure you understand the core mechanics of identifying coefficients and substituting them correctly.

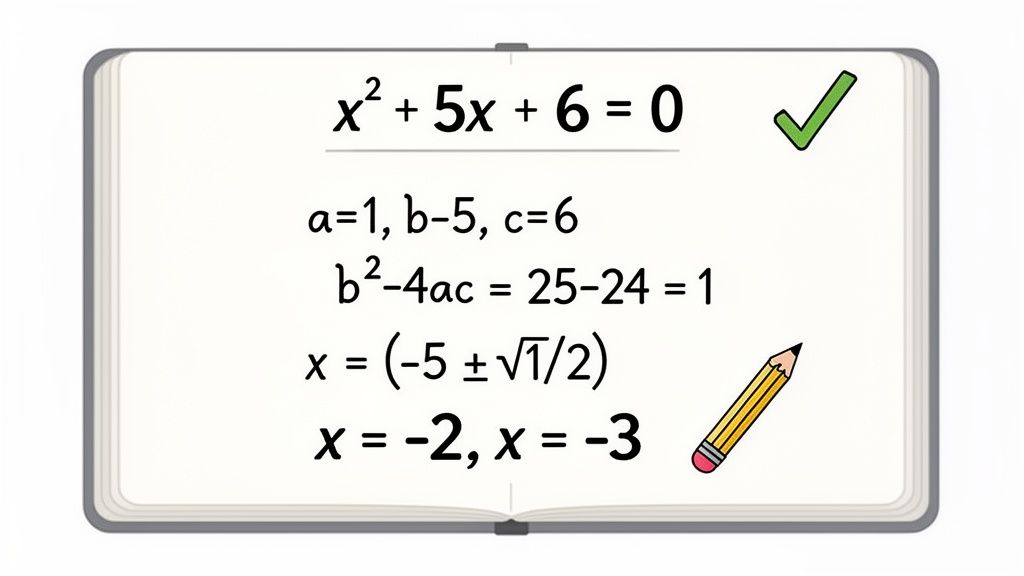
Let's break down one of the most common introductory quadratic formula practice problems: x² + 5x + 6 = 0.

Strategic Breakdown

Solving this problem is a systematic process. The key is to avoid rushing and to handle each component of the formula deliberately.

Step 1: Identify the Coefficients (a, b, c) First, compare your equation to the standard form ax² + bx + c = 0.

• a is the coefficient of the x² term. Here, a = 1.
• b is the coefficient of the x term. Here, b = 5.
• c is the constant term. Here, c = 6.

Step 2: Calculate the Discriminant (b² - 4ac) The discriminant tells you the nature of the roots (solutions). Calculating it separately minimizes errors.

• b² - 4ac = (5)² - 4(1)(6)
• 25 - 24 = 1 Since the discriminant is a positive perfect square (1), we know we will get two distinct, real, and rational solutions.

Step 3: Apply the Full Quadratic Formula Now, substitute the values of a, b, and the discriminant into the formula: x = [-b ± √(b² - 4ac)] / 2a.

• x = [-5 ± √(1)] / 2(1)
• x = (-5 ± 1) / 2

Step 4: Solve for Both Roots Finally, calculate the two possible values for x.

• Solution 1: x = (-5 + 1) / 2 = -4 / 2 = -2
• Solution 2: x = (-5 - 1) / 2 = -6 / 2 = -3

Actionable Takeaways

Key Strategy: Always write down a=, b=, and c= before you start. This simple habit drastically reduces substitution errors, a common pitfall for students new to the formula.

• Verify Your Solutions: Plug x = -2 and x = -3 back into the original equation x² + 5x + 6 = 0 to confirm they are correct. This is a crucial self-checking mechanism.
• Connect to Factoring: Notice that (x + 2)(x + 3) = x² + 5x + 6. For simple problems like this, factoring is often faster. Understanding both methods provides a deeper insight into how to solve quadratic equations.
• Use Digital Tools: If you're stuck, you can use a tool like Feen AI to upload a photo of your work and get guided assistance, helping you spot where you went wrong without just giving you the answer.

2. Discriminant = Zero Problem - One Repeated Real Solution

After mastering the basics, the next critical scenario in our quadratic formula practice problems is when the equation yields just one repeated solution. This occurs when the discriminant, b² - 4ac, is exactly zero. This problem type is essential because it connects the algebraic solution to a specific geometric outcome: a parabola whose vertex touches the x-axis at a single point. It highlights the power of the discriminant in predicting the nature of the solutions before you even finish the formula.

Let’s analyze a classic example of this case: x² - 6x + 9 = 0.

Strategic Breakdown

Solving this type of problem reinforces the importance of the discriminant. The process is identical, but the result is unique and reveals a special kind of quadratic equation.

Step 1: Identify the Coefficients (a, b, c) First, align the equation with the standard ax² + bx + c = 0 form.

• a is the coefficient of the x² term. Here, a = 1.
• b is the coefficient of the x term. Here, b = -6.
• c is the constant term. Here, c = 9.

Step 2: Calculate the Discriminant (b² - 4ac) This step is the most revealing for this problem type. Calculating the discriminant first is a key strategy.

• b² - 4ac = (-6)² - 4(1)(9)
• 36 - 36 = 0 A discriminant of zero is a definitive signal that you will get exactly one real, rational solution.

Step 3: Apply the Full Quadratic Formula Now, substitute your coefficients and the discriminant (0) into the formula: x = [-b ± √(b² - 4ac)] / 2a.

• x = [-(-6) ± √(0)] / 2(1)
• x = (6 ± 0) / 2

Step 4: Solve for the Single Root Since adding or subtracting zero doesn't change the value, the ± part of the formula becomes irrelevant.

• Solution: x = 6 / 2 = 3 This is a single, repeated root.

Actionable Takeaways

Key Strategy: Always calculate the discriminant first. If it's zero, you can predict you'll find only one solution, which simplifies the rest of the calculation and helps you catch potential errors.

• Recognize Perfect Square Trinomials: Notice that x² - 6x + 9 is the expanded form of (x - 3)². Whenever a quadratic is a perfect square trinomial, its discriminant will be zero. Recognizing this pattern can save you time.
• Visualize the Graph: A single repeated solution means the parabola's vertex lies directly on the x-axis. For y = x² - 6x + 9, the graph touches the x-axis at exactly one point: (3, 0). This visual connection deepens understanding.
• Confirm the Solution: Plug x = 3 back into the original equation: (3)² - 6(3) + 9 = 9 - 18 + 9 = 0. The check confirms your answer is correct.

3. Negative Discriminant Problem - Complex Solutions

After mastering real solutions, the next crucial step in your algebraic journey is encountering equations that don't cross the x-axis. These problems introduce the concept of complex numbers by yielding a negative discriminant. This type of quadratic formula practice problem is essential for understanding that "no real solution" does not mean no solution at all; it simply means the solutions exist in the complex plane.

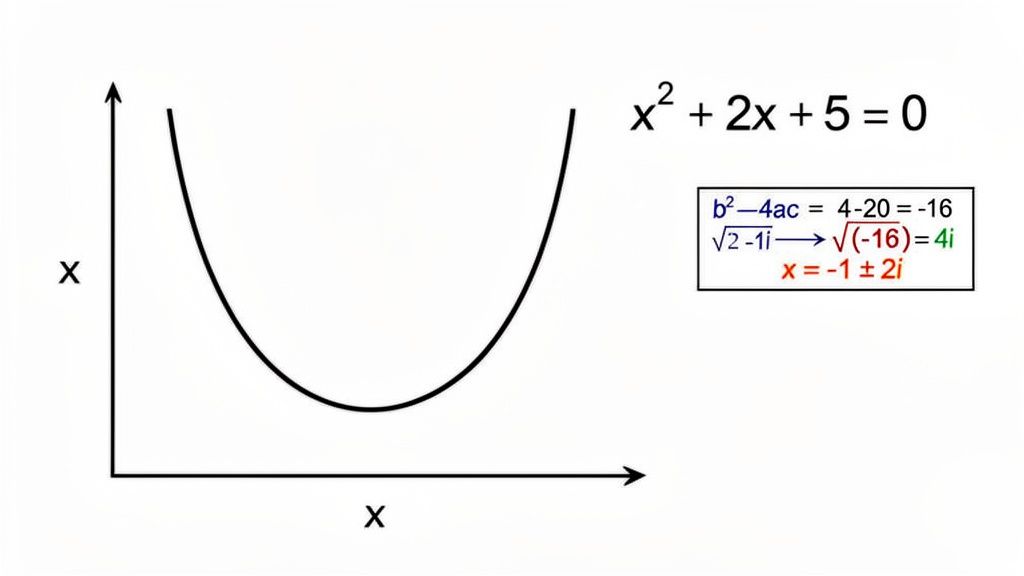
Let's explore a classic example that requires this advanced thinking: x² + 2x + 5 = 0.

Strategic Breakdown

Solving problems with complex roots requires careful handling of negative square roots. The process remains systematic, with an added step for simplifying the imaginary unit.

Step 1: Identify the Coefficients (a, b, c) As always, start by comparing the equation to the standard form ax² + bx + c = 0.

• a is the coefficient of the x² term. Here, a = 1.
• b is the coefficient of the x term. Here, b = 2.
• c is the constant term. Here, c = 5.

Step 2: Calculate the Discriminant (b² - 4ac) This calculation will reveal the nature of the roots. A negative result signals complex solutions.

• b² - 4ac = (2)² - 4(1)(5)
• 4 - 20 = -16 Since the discriminant is negative, we know there are no real solutions. The parabola never intersects the x-axis, and our two solutions will be a complex conjugate pair.

Step 3: Apply the Full Quadratic Formula Substitute the coefficients and the discriminant into the formula: x = [-b ± √(b² - 4ac)] / 2a.

• x = [-2 ± √(-16)] / 2(1)
• Here, we use the rule √(-N) = i√N. So, √(-16) = i√(16) = 4i.
• x = (-2 ± 4i) / 2

Step 4: Solve for Both Complex Roots Simplify the expression to write the solutions in standard complex form a + bi.

• Solution 1: x = (-2 + 4i) / 2 = -1 + 2i
• Solution 2: x = (-2 - 4i) / 2 = -1 - 2i

Actionable Takeaways

Key Strategy: The moment you see a negative discriminant, immediately rewrite the radical using the imaginary unit i. For example, transform √(-16) to 4i before proceeding. This prevents errors and simplifies the final steps.

• Conjugate Pairs are a Rule: For quadratic equations with real coefficients, complex solutions will always appear as conjugate pairs (a + bi and a - bi). If your answers don't form a pair, re-check your calculations.
• Understand the "Why": A negative discriminant means the graph of the parabola does not touch or cross the x-axis. This graphical understanding reinforces why real-number solutions are impossible.
• Applications in STEM: Complex numbers are not just an abstract concept; they are fundamental in fields like electrical engineering for analyzing AC circuits and in quantum mechanics.

4. Fractional Coefficients Problem - Clearing Denominators

Encountering fractions in an algebra problem can be intimidating, but it’s a common scenario in fields like engineering and chemistry. This type of problem, featuring an equation like (1/2)x² + (3/4)x - (1/8) = 0, tests your ability to handle fractional coefficients. The core challenge is deciding whether to work with the fractions directly or to simplify the equation first by clearing the denominators.

This problem builds crucial computational skills with rational numbers. It reinforces that the quadratic formula is a universal tool, capable of solving equations regardless of whether the coefficients are neat integers or complex fractions.

Let's solve the practice problem (1/2)x² + (3/4)x - (1/8) = 0.

Strategic Breakdown

The most efficient strategy here is to eliminate the fractions at the very beginning. This transforms the problem into a more familiar integer-based equation, significantly reducing the chance of arithmetic errors when substituting into the quadratic formula.

Step 1: Clear the Denominators First, find the least common denominator (LCD) of all the fractions. For denominators 2, 4, and 8, the LCD is 8. Multiply every term in the equation by the LCD.

• 8 * [(1/2)x² + (3/4)x - (1/8)] = 8 * 0
• (8/2)x² + (24/4)x - (8/8) = 0
• This simplifies to 4x² + 6x - 1 = 0.

Step 2: Identify the New Coefficients (a, b, c) Now, use the simplified integer-based equation.

• a is the coefficient of the x² term. Here, a = 4.
• b is the coefficient of the x term. Here, b = 6.
• c is the constant term. Here, c = -1.

Step 3: Calculate the Discriminant (b² - 4ac) Calculate the discriminant using the new integer coefficients.

• b² - 4ac = (6)² - 4(4)(-1)
• 36 - (-16) = 36 + 16 = 52 Since the discriminant is positive but not a perfect square, we expect two distinct, real, and irrational solutions.

Step 4: Apply the Full Quadratic Formula Substitute the values of a, b, and the discriminant into the formula: x = [-b ± √(b² - 4ac)] / 2a.

• x = [-6 ± √(52)] / 2(4)
• Simplify the radical: √52 = √(4 * 13) = 2√13
• x = (-6 ± 2√13) / 8
• Factor out a 2 from the numerator: x = 2(-3 ± √13) / 8
• Simplify the fraction to get the final answers: x = (-3 ± √13) / 4

Actionable Takeaways

Key Strategy: Always clear the denominators by multiplying the entire equation by the LCD. This pre-emptive step converts a complex fractional problem into a straightforward integer problem, which is the gold standard for avoiding calculation mistakes.

• Fractions Compound Errors: While it's possible to plug the original fractions into the formula, operations like squaring (3/4) and multiplying 4(1/2)(-1/8) create many opportunities for small arithmetic slips.
• Simplify Radicals: Don't forget to simplify the radical in your final answer. Leaving √52 instead of 2√13 is often considered an incomplete solution.
• Verify with the Original: To be absolutely certain, you can substitute one of your final answers, like x = (-3 + √13) / 4, back into the original fractional equation. It's tedious, but it's a foolproof way to check your work.

5. Large Coefficients Problem - Managing Computation Complexity

As you move beyond introductory examples, you'll encounter quadratic equations where the numbers aren't so friendly. Problems with large coefficients test not just your understanding of the formula but also your organizational skills and computational accuracy. This is where many simple calculation errors occur, making systematic work essential. These types of quadratic formula practice problems are crucial for building the skills needed for real-world applications in fields like physics or economics, where coefficients are rarely small, neat integers.

Let’s tackle a problem that requires careful calculation: 12x² - 47x + 40 = 0.

Strategic Breakdown

With larger numbers, the strategy shifts from speed to precision. Each step must be handled methodically to prevent small mistakes from derailing the entire solution.

Step 1: Identify the Coefficients (a, b, c) Carefully compare the equation to the standard ax² + bx + c = 0 form. Pay close attention to signs.

• a is the coefficient of the x² term. Here, a = 12.
• b is the coefficient of the x term. Here, b = -47.
• c is the constant term. Here, c = 40.

Step 2: Calculate the Discriminant (b² - 4ac) Calculating the discriminant separately is even more critical with large numbers. This isolates the most complex part of the calculation.

• b² - 4ac = (-47)² - 4(12)(40)
• 2209 - 1920 = 289 The discriminant is 289. It's helpful to know common perfect squares; you might recognize that 17² = 289. Since it's a positive perfect square, we expect two distinct, real, and rational solutions.

Step 3: Apply the Full Quadratic Formula Substitute the values of a, b, and the discriminant into the formula: x = [-b ± √(b² - 4ac)] / 2a.

• x = [-(-47) ± √(289)] / 2(12)
• x = (47 ± 17) / 24

Step 4: Solve for Both Roots Now, calculate the two solutions and simplify the resulting fractions.

• Solution 1: x = (47 + 17) / 24 = 64 / 24 = 8/3
• Solution 2: x = (47 - 17) / 24 = 30 / 24 = 5/4

Actionable Takeaways

Key Strategy: Don't rely on mental math for multi-digit calculations. Write out every step, especially when squaring negative numbers and multiplying the 4ac term. A calculator is your friend, but methodical work is your best defense against errors.

• Break It Down: Handle the b² calculation and the 4ac calculation as two separate tasks before subtracting. This reduces the cognitive load and minimizes mistakes.
• Check for Simplification: The final answers, 8/3 and 5/4, required simplifying the fractions 64/24 and 30/24. Always check if your fractional answers can be reduced to their simplest form.
• Use Technology as a Check: After solving by hand, use a tool like the Feen AI platform to verify your calculations. This builds confidence and helps you pinpoint exactly where an error might have occurred without just giving away the solution.

6. Applied Word Problem - Setting Up and Solving

The quadratic formula extends far beyond abstract math, serving as a powerful tool for modeling real-world scenarios. This type of problem challenges you to translate a narrative into a mathematical equation and then solve it. It's where theory meets practice, showing you why mastering the formula is essential for fields like physics, engineering, and finance.

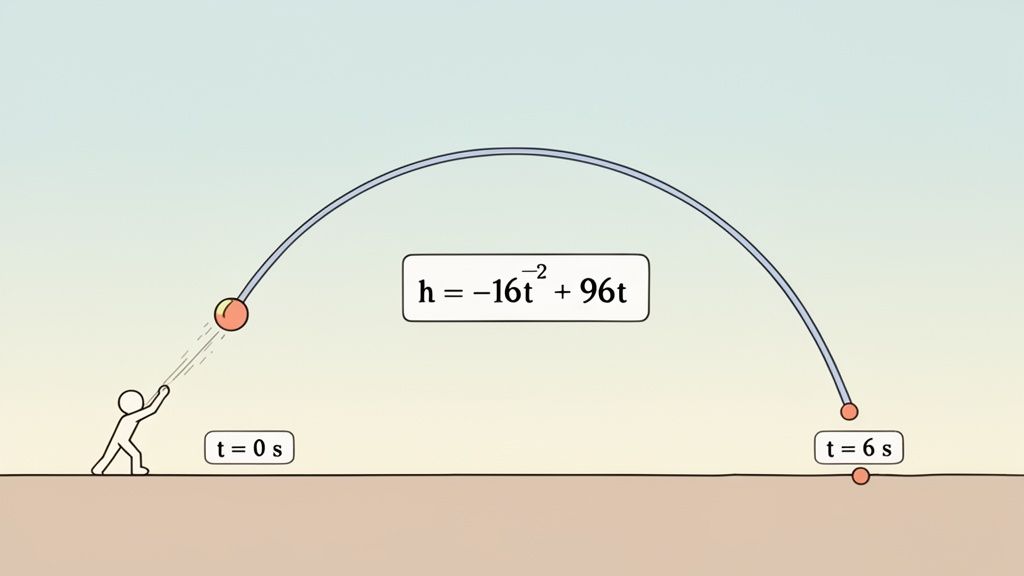
Let's tackle a classic projectile motion problem: "A projectile is launched upward from ground level with an initial velocity of 96 ft/s. The height h after t seconds is given by the equation h = -16t² + 96t. When does the projectile return to the ground?"

Strategic Breakdown

Success with word problems hinges on careful translation and interpretation. The goal is to convert the question into a standard quadratic equation you can solve.

Step 1: Translate the Question into an Equation The problem asks when the projectile "returns to the ground." Ground level corresponds to a height of h = 0. So, we set the given equation equal to zero:

• 0 = -16t² + 96t
• Or, rearranging to the standard form: -16t² + 96t + 0 = 0

Step 2: Identify the Coefficients (a, b, c) Compare -16t² + 96t + 0 = 0 to the standard form ax² + bx + c = 0. Here, our variable is t instead of x.

• a = -16
• b = 96
• c = 0

Step 3: Apply the Full Quadratic Formula Substitute these coefficients into the formula: t = [-b ± √(b² - 4ac)] / 2a.

• t = [-96 ± √(96² - 4(-16)(0))] / 2(-16)
• t = [-96 ± √(9216 - 0)] / -32
• t = [-96 ± √9216] / -32
• t = (-96 ± 96) / -32

Step 4: Solve for Both Roots and Interpret the Results Calculate the two possible values for t and consider what they mean in the context of the problem.

• Solution 1: t = (-96 + 96) / -32 = 0 / -32 = 0
• Solution 2: t = (-96 - 96) / -32 = -192 / -32 = 6

The two solutions are t = 0 seconds (the moment of launch) and t = 6 seconds (the moment it lands). The question asks when it returns to the ground, so the answer is 6 seconds.

Actionable Takeaways

Key Strategy: The most critical step in any word problem is translating the "ask" into a mathematical expression. "Returns to the ground" is the verbal cue for "set h = 0."

• Interpret Both Solutions: The quadratic formula often gives two answers. Always ask yourself if both make sense in the real world. A negative time, for instance, would likely be an invalid solution.
• Simplify First: In this case, we could have factored out -16t from -16t² + 96t = 0 to get -16t(t - 6) = 0, yielding t=0 and t=6 much faster. Recognizing this connection is a key part of becoming proficient with quadratic formula practice problems.
• Build Foundational Skills: If translating words to equations is a challenge, strengthening those skills is crucial. You can find more guidance on how to master the process by learning how to solve word problems in algebra.

7. Irrational Solutions Problem - Simplifying Radicals

Not every quadratic equation yields neat, integer solutions. Often, you'll encounter problems where the discriminant is positive but not a perfect square. This leads to irrational solutions, a crucial concept that bridges the gap between simple algebra and its application in geometry and higher mathematics. Mastering these problems requires a firm grasp of simplifying radicals.

These types of quadratic formula practice problems test not just your ability to apply the formula, but also your precision in handling square roots. Let's work through a classic example: x² - 6x + 7 = 0.

Strategic Breakdown

Solving problems with irrational roots demands careful attention to simplification. The process is straightforward, but one missed step in simplifying the radical can lead to an incorrect final answer.

Step 1: Identify the Coefficients (a, b, c) As always, start by comparing the equation to the standard form ax² + bx + c = 0.

• a is the coefficient of the x² term. Here, a = 1.
• b is the coefficient of the x term. Here, b = -6.
• c is the constant term. Here, c = 7.

Step 2: Calculate the Discriminant (b² - 4ac) Calculate the value under the square root first to determine the nature of the roots.

• b² - 4ac = (-6)² - 4(1)(7)
• 36 - 28 = 8 Since the discriminant (8) is positive but not a perfect square, we know we will get two distinct, real, and irrational solutions.

Step 3: Apply the Full Quadratic Formula Substitute the coefficients and the discriminant into the formula: x = [-b ± √(b² - 4ac)] / 2a.

• x = [-(-6) ± √(8)] / 2(1)
• x = [6 ± √8] / 2

Step 4: Simplify the Radical and Reduce the Fraction This is the critical step. The radical √8 must be simplified.

• Find the largest perfect square that divides 8. In this case, it's 4.
• Rewrite the radical: √8 = √(4 * 2) = √4 * √2 = 2√2.
• Substitute back into the equation: x = (6 ± 2√2) / 2.
• Now, factor out the common term (2) in the numerator and reduce the fraction: x = 2(3 ± √2) / 2.
• Final Solutions: x = 3 + √2 and x = 3 - √2.

Actionable Takeaways

Key Strategy: Always check if the number under the radical can be simplified. Look for perfect square factors (4, 9, 16, 25, 36, etc.). This is the most common place where points are lost.

• Write Answers in Standard Form: Express your final answers in the simplified form a ± b√c, where c has no perfect square factors other than 1. This is the conventional format for irrational solutions.
• Check for Reducibility: After simplifying the radical, always check if all three terms (the number outside the radical, the coefficient of the radical, and the denominator) share a common factor. If so, you can reduce the entire expression.
• Connect to Geometry: Irrational solutions frequently appear in geometric problems, such as finding the side lengths of a rectangle with a given area and perimeter, or in problems involving the Pythagorean theorem.

8. Multi-Step Equation Problem - Rearranging to Standard Form

Not all quadratic equations are handed to you in the neat ax² + bx + c = 0 format. Often, you'll encounter problems where terms are scattered on both sides of the equals sign. This problem type is designed to test a crucial preliminary skill: algebraic manipulation. Before you can even think about the quadratic formula, you must first rearrange the equation into standard form.

This step is fundamental because the values of a, b, and c are only meaningful when the equation is set equal to zero. Let's work through a common example of these quadratic formula practice problems: 3x² + 5x = 2x + 8.

Strategic Breakdown

The core strategy here is to methodically clean up the equation before applying the formula. This two-phase approach prevents the most common errors associated with this problem type.

Step 1: Rearrange the Equation into Standard Form (ax² + bx + c = 0) Your first goal is to move all terms to one side of the equation to set it equal to zero. It's conventional to keep the ax² term positive.

• Start with: 3x² + 5x = 2x + 8
• Subtract 2x from both sides: 3x² + 5x - 2x = 8
• Subtract 8 from both sides: 3x² + 5x - 2x - 8 = 0
• Combine like terms: 3x² + 3x - 8 = 0

Step 2: Identify the New Coefficients (a, b, c) Now that the equation is in standard form, you can correctly identify the coefficients.

• a is the coefficient of the x² term. Here, a = 3.
• b is the coefficient of the x term. Here, b = 3.
• c is the constant term. Here, c = -8. (Don't forget the negative sign!)

Step 3: Calculate the Discriminant (b² - 4ac) Calculate the value inside the square root separately to stay organized.

• b² - 4ac = (3)² - 4(3)(-8)
• 9 - (-96) = 9 + 96 = 105 Since the discriminant is 105 (a positive non-perfect square), we expect two distinct, real, and irrational solutions.

Step 4: Apply the Full Quadratic Formula Substitute a, b, and the discriminant into the formula: x = [-b ± √(b² - 4ac)] / 2a.

• x = [-3 ± √(105)] / 2(3)
• x = (-3 ± √105) / 6

Step 5: State the Final Solutions The solutions are left in their exact, radical form as √105 cannot be simplified further.

• Solution 1: x = (-3 + √105) / 6
• Solution 2: x = (-3 - √105) / 6

Actionable Takeaways

Key Strategy: Your first reflex for any quadratic equation should be: "Get everything to one side, set it equal to zero." This non-negotiable first step ensures you are working with the correct a, b, and c values.

• Double-Check Your Algebra: A simple sign error during rearrangement will completely alter the outcome. After moving terms, quickly check that your addition and subtraction were done correctly.
• Master the Process: This rearrangement skill is not just for quadratic equations; it's a core component of algebra. Understanding how to isolate and combine terms is essential for almost any advanced math problem. For a deeper dive, explore guides on how to solve math problems step-by-step.
• Embrace Irrational Answers: Don't be alarmed by answers containing radicals like √105. In higher-level math and real-world physics problems, tidy integer solutions are the exception, not the rule.

8-Problem Quadratic Formula Comparison

Example	Implementation Complexity	Resource Requirements	Expected Outcomes	Ideal Use Cases	Key Advantages
Basic Quadratic Formula Problem (x² + 5x + 6 = 0)	Low	Paper, basic calculator	Two distinct real integer solutions; easily verifiable by factoring	Introductory lessons and formula practice	Simple arithmetic; high success rate; reinforces coefficient ID
Discriminant = Zero Problem (x² - 6x + 9 = 0)	Low	Paper, graphing optional	One repeated real root (multiplicity 2); perfect square trinomial	Teaching discriminant cases and vertex interpretation	Clarifies discriminant meaning; links algebra and graph
Negative Discriminant Problem (x² + 2x + 5 = 0)	Medium	Knowledge of complex numbers, calculator helpful	Complex conjugate solutions (no real roots)	Intro to complex numbers; higher‑level applications	Demonstrates imaginary units; prepares for advanced topics
Fractional Coefficients Problem ((1/2)x² + (3/4)x - 1/8 = 0)	Medium	Strong fraction skills, option to clear denominators, calculator	Real solutions after fraction manipulation; practice rational arithmetic	Fraction fluency exercises; applied measurement problems	Teaches clearing denominators; reinforces rational computation
Large Coefficients Problem (12x² - 47x + 40 = 0)	Medium–High	Reliable calculator, careful written work	Real solutions (may be fractional/irrational); higher computation load	Realistic application problems and test prep	Builds organization, error‑checking, and computational stamina
Applied Word Problem (h = -16t² + 96t)	Medium	Context comprehension, unit tracking, modeling skills	Contextual solutions with interpretation (reject extraneous roots)	STEM modeling, applied problem solving	Connects math to real world; develops interpretation skills
Irrational Solutions Problem (x² - 6x + 7 = 0)	Medium	Radical simplification skills, calculator optional	Irrational real solutions expressed in simplified radical form	Radical practice; standardized test preparation	Reinforces simplifying radicals and reducing expressions
Multi‑Step Equation Problem (3x² + 5x = 2x + 8)	Low–Medium	Algebra manipulation skills, careful term collection	Correct standard form ax² + bx + c = 0 then solutions	Instruction on equation setup and avoiding setup errors	Emphasizes prerequisite rearrangement and sign care

Key Takeaways and Your Next Steps in Algebra

Congratulations on working through our comprehensive set of quadratic formula practice problems. By tackling each example, from straightforward equations to complex word problems, you have built a robust and flexible understanding of one of algebra's most powerful tools. This journey was about more than just finding x; it was about developing a strategic mathematical mindset.

The core lesson is that the quadratic formula is a process, not just a plug-and-chug equation. It requires precision, analytical thinking, and a clear strategy before you even begin to calculate. Mastery comes from recognizing the patterns and nuances within each problem type.

Your Strategic Toolkit: A Recap

Reflect on the key strategies you've practiced. You’ve moved beyond rote memorization and can now approach quadratic equations with a strategic eye. The goal is to make these analytical steps second nature.

Here are the essential takeaways from the practice problems you've conquered:

• Pre-Analysis is Crucial: Before substituting values, always identify a, b, and c and calculate the discriminant (b² - 4ac). This single step tells you whether to expect two real, one real, or two complex solutions, preventing surprises later on.
• Simplify First, Calculate Later: When faced with fractional or large coefficients, your first move should be simplification. Clearing denominators or factoring out a greatest common divisor makes the subsequent calculations much more manageable and less prone to error.
• Standard Form is Non-Negotiable: The quadratic formula only works when the equation is in the standard form ax² + bx + c = 0. As seen in the multi-step problem, your initial and most critical task is often algebraic manipulation to achieve this form.
• Context is King in Word Problems: For applied problems, the challenge isn't the formula itself but the translation of a real-world scenario into a mathematical equation. The key is to define your variable, set up the equation logically, and then critically evaluate your solutions to see if they make sense in the context of the problem (e.g., negative length is impossible).

Key Insight: True mastery of the quadratic formula isn't about solving one problem; it's about developing a reliable process that works for any quadratic equation you encounter. It’s about building the confidence to dissect, simplify, and solve with precision.

Charting Your Path Forward

So, what comes next? The journey to mathematical fluency is built on consistent, deliberate practice. Don't let your momentum fade. Here are actionable steps to solidify your skills and continue your growth in algebra.

1. Revisit and Review: Return to any problem in this guide that gave you trouble. Rework it from scratch without looking at the solution until you are finished. This reinforces the specific skill that was a weak point.
2. Mix It Up: Don't just practice one problem type at a time. Find mixed problem sets that force you to first identify the best solution method. Should you use the quadratic formula, factor, or complete the square? This decision-making process is a vital advanced skill.
3. Embrace Active Learning: To truly cement these concepts, you need to be an active participant in your learning. Staying focused, especially in a digital environment, is a skill in itself. Exploring proven tips for student engagement in online learning can transform your study sessions from passive review into powerful, active learning experiences.
4. Seek Out New Challenges: Look for more advanced applications of quadratic equations in physics (projectile motion), economics (profit maximization), or geometry. Applying the formula to different disciplines will deepen your appreciation for its versatility and power.

By consistently applying these strategies, you are not just preparing for your next quiz or exam. You are building foundational problem-solving skills that are essential in STEM fields, finance, and any area that requires rigorous analytical thought. Keep practicing, stay curious, and remember that every problem you solve is another step toward becoming a confident and capable mathematician.

---

Feeling stuck on a tough problem or need instant clarification on a specific step? Don't let frustration halt your progress. Feen AI is your on-demand AI homework helper, ready to guide you through complex quadratic formula practice problems and beyond. Upload a picture of your work, and get step-by-step assistance to understand the process, not just the answer. Feen AI