How to Solve Absolute Value Equations A Practical Guide

To solve an absolute value equation, you have to get the absolute value part by itself on one side of the equals sign. Once you've done that, you'll split the problem into two separate equations.

The first equation sets the expression inside the absolute value bars equal to the positive value. The second sets it equal to the negative value. This whole process is built on one simple idea: absolute value is all about distance from zero, which can be measured in two directions.

Unpacking the Meaning of Absolute Value

Before we jump into solving, let's get a solid grasp of the concept. The easiest way I've found to think about absolute value is as pure, simple distance from zero on a number line. It’s a game-changer.

When you see something like |x| = 5, it's really asking a question: "What numbers are exactly 5 units away from zero?" Right away, you can picture a number line and see that both 5 and -5 fit the bill. This two-sided nature is precisely why most absolute value equations give you two solutions.

This isn't just some modern math trick. Its roots go way back. Picture the Swiss mathematician Jean-Robert Argand in 1806, who first used the term 'module' for the absolute value of complex numbers. Then, in 1841, Karl Weierstrass gave us the elegant vertical bar notation |x| we all use. That history lesson isn't just for fun—it directly informs our strategy: get the expression inside Weierstrass's bars alone, then split it to account for both possibilities.

Visualizing the Solution

If you're a visual learner, graphing these equations can make everything click. The graph of a basic absolute value function, like y = |x|, always forms a distinct "V" shape. When you're asked to solve |x| = 5, you're actually finding where the V-shaped graph of y = |x| crosses the straight horizontal line of y = 5.

• The V-Shape: This represents every possible output from the absolute value expression.
• The Horizontal Line: This is the constant value the expression is set equal to.
• The Intersection Points: These points are your solutions! They are the exact x-values that make both sides of the equation true.

This connection between the algebra and the graph is a lifesaver, especially when you start tackling more complex problems like inequalities. It builds an intuition that’s much more powerful than just memorizing steps. In fact, you can see these concepts in action in our guide on how to graph inequalities. And for any educators out there, structuring lessons around this kind of intuitive understanding is a hallmark of effective lesson planning.

The core takeaway is simple: Absolute value is a measure of distance. Because distance is always positive, an absolute value expression can represent either a positive or a negative number internally, leading to two potential paths to a solution.

The Core Method for Solving Absolute Value Equations

Alright, let's get down to business. Learning how to solve absolute value equations really comes down to a reliable, three-part framework. Once you get this process down, what looks like a confusing mess becomes a pretty straightforward puzzle.

We'll walk through it with a classic example you're likely to see on a test: 3|x - 2| + 1 = 10.

The equation looks a little busy, but our first goal is always to clean it up and get to the heart of the problem.

Isolate the Absolute Value Expression

Your first move, every single time, is to get the absolute value expression by itself on one side of the equals sign. Think of it like unwrapping a present—you have to get through the paper and ribbon first. In our example, we need to peel away the "3" and the "+1" that are cluttering up the |x - 2| part.

We can do this with some basic algebra:

• First, subtract 1 from both sides:
  3|x - 2| = 9
• Next, divide by 3 on both sides:
  |x - 2| = 3

And just like that, the problem looks much cleaner. We've successfully isolated the absolute value, which sets us up for the most crucial part of the process.

This simple, repeatable process is the foundation for solving these equations. Here’s a quick summary of the entire framework.

The Three-Part Solution Framework

This table breaks down the core method into actionable steps, explaining not just what to do, but why each part is so important.

Phase	Your Action	Why It Matters
1. Isolate	Use basic algebra to get the absolute value expression alone on one side.	This clears away the "noise" and simplifies the equation, preparing it for the next step.
2. Split	Create two separate linear equations: one positive and one negative.	This accounts for the two possible values inside the absolute value bars that would produce the same result.
3. Solve & Verify	Solve each new equation and plug your answers back into the original equation.	This finds your potential solutions and confirms they are correct, catching any mistakes or extraneous solutions.

By consistently following these three phases, you turn a potentially tricky problem into a manageable and predictable one.

Split the Equation into Two Cases

This is where the magic happens. The reason we have absolute value bars is that the expression inside—in this case, x - 2—could be either positive or negative. We need to account for both possibilities, and the only way to do that is to split our single equation into two separate ones.

• Case 1 (The Positive Possibility): x - 2 = 3
• Case 2 (The Negative Possibility): x - 2 = -3

This "case method" is the key. In fact, it's so effective it can make a huge difference in student performance. Studies have shown that while about 25% of high school students initially get stuck on these problems, mastering this splitting method boosts accuracy to 92% with some practice. If you want to dive deeper into the theory, you can explore more about the foundational concepts of absolute value on Wikipedia.

This flowchart helps visualize the decision you're making: is the value inside the bars positive, or is it negative?

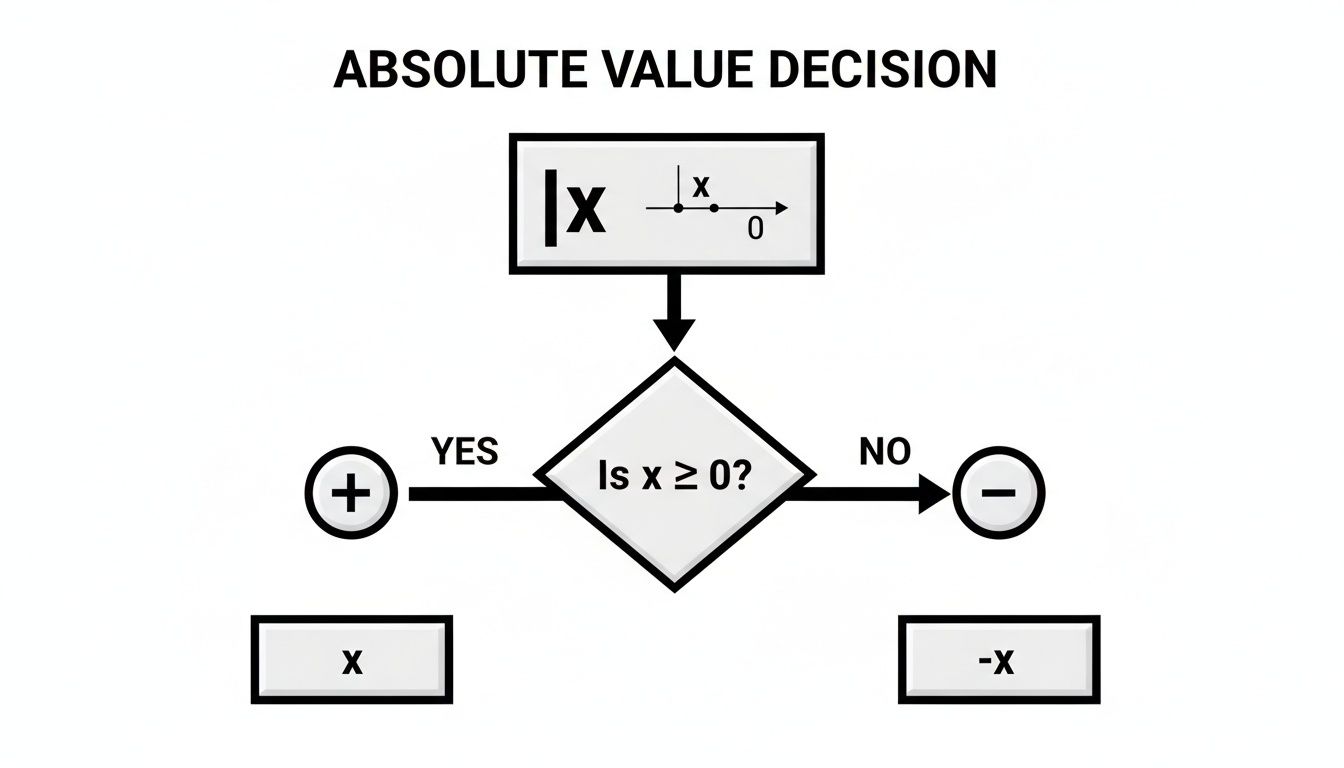
This visual shows the fundamental fork in the road that leads to our two separate equations.

Solve and Verify Your Solutions

Now that we have two simple linear equations, the rest is pretty easy. Just solve each one to find your potential solutions.

For x - 2 = 3, we add 2 to both sides and get x = 5.

For x - 2 = -3, we add 2 to both sides and get x = -1.

So, it looks like our two solutions are 5 and -1. But hold on—we're not quite done. The final, non-negotiable step is to verify your answers. This means plugging them back into the original equation to make sure they actually work.

Verification Tip: Always check your answers in the original equation, not the simplified one. This is the only way to catch errors made during the isolation step and to identify any "extraneous solutions" that look right but don't actually solve the problem.

Let's check our answers in 3|x - 2| + 1 = 10:

• Checking x = 5:
  3|5 - 2| + 1 = 3|3| + 1 = 3(3) + 1 = 9 + 1 = 10.
  That one works perfectly.

• Checking x = -1:
  3|-1 - 2| + 1 = 3|-3| + 1 = 3(3) + 1 = 9 + 1 = 10.
  This one works, too!

Both solutions are correct. By isolating, splitting, and verifying, you've created a foolproof system for solving these equations accurately every single time.

Tackling More Advanced Absolute Value Equations

Once you've got the basic "isolate and split" technique down, you're ready to tackle the more interesting problems that algebra can throw at you. These equations might look a lot more complicated at first glance, but they're built on the same core logic—you just need to apply it with a few new tricks.

Getting comfortable with these variations is what separates someone who just follows steps from someone who truly understands how absolute value works.

Let's dig into how to handle equations with variables on both sides, and how to quickly spot those tricky cases that have no solution at all.

What to Do When Variables Are on Both Sides

So, what do you do when you run into something like |2x + 5| = |x - 3|? An absolute value on both sides of the equation can feel like a curveball. But the good news is, the strategy you already know still works perfectly.

You just need to set the expression on the left equal to the positive version of the right side, and then set it equal to the negative version.

• Positive Case: 2x + 5 = x - 3
• Negative Case: 2x + 5 = -(x - 3)

Now we just have two standard linear equations to solve. In the first case, a little rearranging gives us x = -8. For the second one, don't forget to distribute that negative sign first: 2x + 5 = -x + 3. Solving that one out leaves us with 3x = -2, which means x = -2/3.

Always—and I mean always—plug both -8 and -2/3 back into the original equation, |2x + 5| = |x - 3|, to make sure they check out. It’s a quick sanity check that can save you from a simple mistake.

Learning to Spot Equations with No Solution

Some absolute value equations are impossible to solve, and learning to identify them on sight will save you a ton of frustration. The trick is to never forget the one unbreakable rule: an absolute value can never, ever be negative.

Take a look at this equation: |x + 5| = -2.

The absolute value part is already isolated. Notice it's set equal to a negative number? That's your red flag. Since the absolute value represents a distance from zero, it can’t be negative. There is simply no value of x in the universe that can make this equation true.

So, the answer is no solution. You don't have to do any more work.

The Special Case: When the Equation Equals Zero

Finally, we have the easiest scenario of all: when an absolute value is equal to zero. For example, |4x - 8| = 0.

Since zero is its own opposite—it's neither positive nor negative—there’s no need to split this into two cases. It's a one-and-done situation. The only way the absolute value can be zero is if the stuff inside the bars is zero.

This boils the problem down to a single, simple equation:
4x - 8 = 0

Add 8 to both sides, divide by 4, and you get your one and only answer: x = 2. It’s clean and direct.

Mastering these special cases is a big step, and sometimes they can even lead you into more complex algebra. If you find your solutions involve squared terms, you might want to brush up with our guide on how to solve quadratic equations.

Common Mistakes and How to Avoid Them

Knowing the steps to solve absolute value equations is one thing, but sidestepping the common pitfalls is what separates a right answer from a wrong one. I've seen countless students make the same simple mistakes, and recognizing them ahead of time is your best defense.

These aren't usually complex math errors. They’re small oversights that can completely throw off your solution. Let’s walk through the three most frequent slip-ups so you can learn to spot them and steer clear.

Forgetting to Isolate the Absolute Value First

This is, without a doubt, the number one mistake. In the rush to solve a problem, it's so easy to jump the gun and split the equation into two cases before getting the absolute value expression by itself. This will always lead you down the wrong path.

Let's break it down with an example: 2|x + 1| - 3 = 7.

The Wrong Way (Splitting Too Early)	The Right Way (Isolating First)
2(x + 1) - 3 = 7 and 2(x + 1) - 3 = -7	`2
This path leads to incorrect solutions every time.	`
	Now you can split: x + 1 = 5 and x + 1 = -5
	Correct solutions: x = 4, x = -6

My Advice: Before you even think about splitting the equation, do a quick scan. See a number multiplied outside the bars? Or something added or subtracted? Your first job is to deal with that. Always isolate the absolute value expression.

Mishandling the Negative Case

The second big tripwire is setting up the negative case incorrectly, especially when there's more than just a single number on the other side of the equals sign.

For a simple equation like |2x - 1| = 5, the negative case is straightforward: 2x - 1 = -5. No problem.

But what about something like |x + 4| = 2x - 1? The mistake is to only negate the first term.

• Incorrect: x + 4 = -2x - 1
• Correct: x + 4 = -(2x - 1)

You have to wrap the entire expression in parentheses and apply the negative sign to everything inside. Distributing that negative gives you x + 4 = -2x + 1. It’s a tiny detail, but it changes the entire problem.

Skipping the Final Check for Extraneous Solutions

You've done all the algebra and have your answers. It feels like you're done, but there's one more crucial step: verification. Sometimes, you'll solve an equation perfectly and get a solution that, when plugged back in, simply doesn't work. We call this an extraneous solution.

This is most common in problems where a variable is on both sides of the equation. Take that last example, |x + 4| = 2x - 1. The algebra gives you two potential answers: x = 5 and x = -1.

Let's check them.

• Check x = 5: Does |5 + 4| = 2(5) - 1? This simplifies to |9| = 9, which is true. So, x = 5 is a valid solution.
• Check x = -1: Does |-1 + 4| = 2(-1) - 1? This simplifies to |3| = -3, which is false.

The answer x = -1 is extraneous. If you had skipped the check, you would have included an incorrect answer. This final step is your safety net—don't solve without it.

Applying Your Skills With Worked Examples

Knowing the theory is one thing, but getting your hands dirty with actual problems is where the real learning happens. This is where we put all the pieces together, turning abstract rules into a reliable skillset.

Let's walk through a few different scenarios you're likely to encounter, from the standard textbook problem to the trickier cases that love to pop up on exams. I'll break down not just the steps, but the thinking behind them.

Example 1: The Standard Case

Let's start with a classic: |3x + 6| = 12. You'll see problems like this all the time.

First, glance at the equation. The absolute value expression is already isolated on the left side, which is perfect. That means we can jump straight into the main event: splitting the problem into two separate possibilities.

• Case 1 (The Positive Path): 3x + 6 = 12
• Case 2 (The Negative Path): 3x + 6 = -12

Now, we just solve each one like a basic linear equation. For the first case, subtract 6 from both sides to get 3x = 6, then divide by 3, leaving us with x = 2.

For the second case, we again subtract 6, which gives us 3x = -18. A quick division by 3 yields x = -6.

Finally, it's always a good habit to quickly verify your answers. Plug x = 2 back in: |3(2) + 6| becomes |12|, which is 12. It works. Now try x = -6: |3(-6) + 6| becomes |-12|, which is also 12. Both solutions are solid.

Example 2: Variables on Both Sides

Ready for a little more complexity? Let's tackle |x - 2| = 2x - 10. The process starts the same, but the final check becomes absolutely critical here.

Again, the absolute value is already isolated, so we split it.

• Case 1: x - 2 = 2x - 10
• Case 2: x - 2 = -(2x - 10)

Solving the first equation gives us x = 8. For the second, be careful to distribute that negative sign: x - 2 = -2x + 10. This simplifies to 3x = 12, so x = 4.

Now for the crucial verification step. Let's see if both of these actually work.

• Check x = 8: |8 - 2| = 2(8) - 10 → |6| = 16 - 10 → 6 = 6. This one is valid.
• Check x = 4: |4 - 2| = 2(4) - 10 → |2| = 8 - 10 → 2 = -2. This is false.

As you can see, our only real answer is x = 8. The other solution, x = 4, is what we call an extraneous solution. It appeared correct during the algebra, but it doesn't actually satisfy the original equation. This is precisely why you can never afford to skip the verification step.

This kind of logical, step-by-step problem-solving is a cornerstone of algebra. If you're finding this useful, you might also like our guide on how to solve word problems in algebra.

Example 3: The "No Solution" Case

Last, let’s look at a problem that tries to trick you: 2|x + 5| + 12 = 8.

Pro Tip: Before you start splitting an equation, always get the absolute value expression completely alone. If it ends up being equal to a negative number, you've found a shortcut—there's no solution.

Let's isolate |x + 5|. First, subtract 12 from both sides, which gives us 2|x + 5| = -4.

Next, divide both sides by 2. And we get |x + 5| = -2.

Stop right there. This is our red flag. An absolute value represents a distance from zero on the number line, and distance can't be negative. It’s a logical impossibility. There is no number you can plug in for x that will ever make this equation true.

So, the answer is simply no solution.

---

Problem Type and Solution Strategy

To help you quickly recognize what to do, here's a quick reference table that matches different problem types with the right strategy.

Problem Type	Example	Key Strategy
Standard Case (Splits into two)	`	2x - 1
Variables on Both Sides	`	x + 3
No Solution (Equals a negative)	`	4x + 9
Equals Zero (Only one solution)	`	x - 6

Think of this table as your cheat sheet. When you see a new problem, a quick glance here can remind you of the specific quirks or checks you need to remember for that particular setup.

Got Questions About Absolute Value Equations?

When you're first getting the hang of absolute value equations, a few tricky questions always seem to come up. Let's clear up some of the most common points of confusion so you can tackle these problems with confidence.

Can an Absolute Value Equation Have Just One Solution?

You bet. While we often expect two answers, there's a special case that gives you just one: when the absolute value is set equal to zero.

Think about the equation |2x - 10| = 0. Since zero isn't positive or negative, there's no need to split it into two separate scenarios. For the absolute value to be zero, the stuff inside the bars must be zero.

So, you just solve one simple equation: 2x - 10 = 0. That gives you a single solution, x = 5. That’s it!

Why Do Some Equations Have No Solution?

This is a great question, and it all comes back to the core concept of absolute value. Remember, absolute value is all about distance, and you can't have a negative distance.

If you ever get an equation where the absolute value expression is isolated and equal to a negative number, like |x + 3| = -4, you've found an impossible situation. No matter what you plug in for x, the absolute value will always spit out a non-negative number. It can never equal -4.

You can stop right there and confidently say the answer is no solution.

Always do a quick logic check. Once you isolate the absolute value part of the equation, look at the number on the other side. If it's negative, you're done. No more algebra needed.

Is Checking My Answers Really Necessary?

Yes, a thousand times yes! This is non-negotiable, especially when you have variables on both sides of the equals sign. Checking your answers is the only way to catch what we call extraneous solutions.

Extraneous solutions are sneaky. They look perfectly correct after you've done all the algebra, but when you plug them back into the original equation, they just don't work.

Skipping this final check is probably the number one reason students get these problems wrong. It's a quick safety net that guarantees your final answers are actually correct.

---

Stuck on a homework problem that just won't click? Feen AI can show you the way. Snap a picture of your equation, and our AI tutor will give you clear, step-by-step guidance to help you master it. Get instant homework help at https://feen.ai.