How to Solve Limits in Calculus: Practical Guide how to solve limits in calculus

Before you even think about pulling out any fancy algebraic maneuvers, your first move with any limit should always be the same: direct substitution. It's the most straightforward approach, and you'd be surprised how often it gives you the answer right away. Think of it as the foundation for everything else.

Your First Move When Solving Any Limit

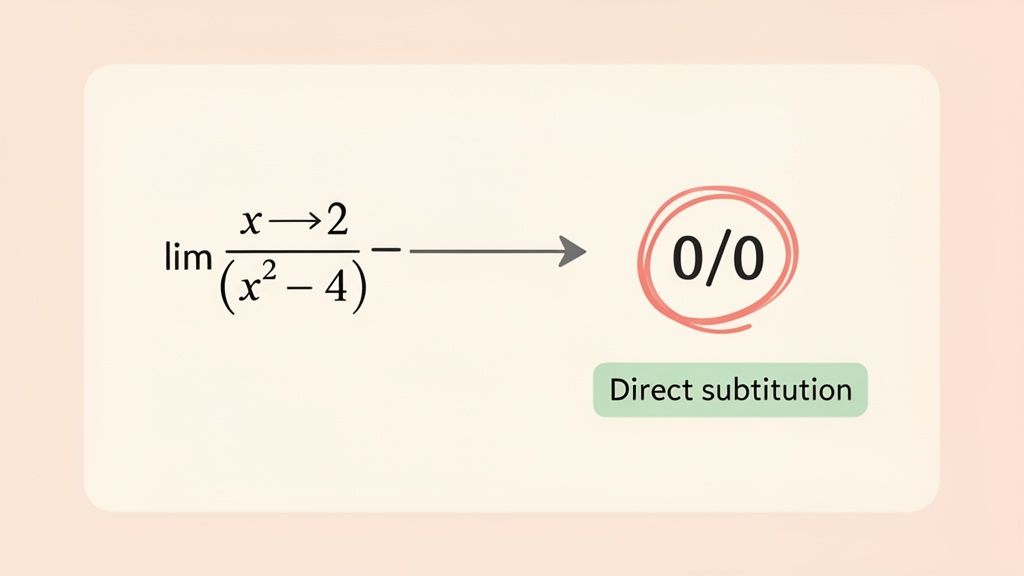
When you're staring down a limit problem, the most efficient way to start is just to plug the value x is approaching directly into the function. It’s a low-effort, high-reward strategy that works beautifully for many functions, especially continuous ones like polynomials.

Let's say you're asked to find the limit of f(x) = 2x + 1 as x approaches 3. All you have to do is substitute 3 for x. The math is simple: 2(3) + 1 = 7. The limit is 7. Done. It works because the function's value at that point is exactly what it's approaching.

When Substitution Works Perfectly

Direct substitution is your best friend when dealing with functions that are continuous at the point you're interested in. This includes a lot of common functions:

• Polynomials: Functions like x² − 4x + 2 are continuous absolutely everywhere.
• Rational Functions: These are just fractions of polynomials, like (x+5)/(x-2), as long as the denominator doesn't become zero at your limit point.
• Trigonometric, Exponential, and Logarithmic Functions: These guys are also continuous within their own domains.

For example, to find the limit of (x²+1)/(x-4) as x approaches 2, just plug in the 2. You get (2²+1)/(2-4), which simplifies to 5/(-2), or -2.5. You got a real number, so that's your answer. Easy.

The real point of direct substitution is to quickly see if you can solve the limit without the heavy lifting. If you get a defined number, you're done. If you don't, the result you get is a crucial clue that tells you exactly which strategy to use next.

Recognizing the Indeterminate Form

The true power of this first step often reveals itself when it doesn't work. If you plug in the value and end up with the fraction 0/0, you've hit what's called an indeterminate form. This doesn't mean the limit is zero or undefined. Instead, it's a giant signpost telling you there's more work to do.

A 0/0 result usually signals that there's a "hole" in the graph at that exact point. To find the true limit, you'll need to use algebraic techniques like factoring or multiplying by the conjugate to simplify the expression first.

Of course, before diving into complex algebra, it helps to have a clear head. Taking a moment to increase your focus and concentration can make a huge difference in spotting the right path forward and avoiding simple mistakes.

Here's a quick rundown of what to do based on what you get from that first substitution attempt.

Direct Substitution Outcomes and Next Steps

This table gives you a clear game plan. Once you plug in your value for x, find your result in the first column to see what it means and what to do next.

Substitution Result	What It Means	Recommended Next Action
A Real Number (e.g., 5, -1/2)	The function is continuous at that point.	You've found the limit. No further steps are needed.
0/0	Indeterminate form; a hole likely exists.	Use algebraic methods (factoring, conjugate) or L'Hôpital's Rule.
(Non-zero Number)/0	A vertical asymptote exists at this point.	The limit is likely ∞, -∞, or does not exist (DNE).

Think of this table as your roadmap. That initial substitution isn't just a guess; it's a diagnostic tool that points you toward the correct problem-solving technique.

Using Algebra to Crack Indeterminate Forms

So you’ve plugged in the number and hit the dreaded 0/0. Your first instinct might be to think it's unsolvable, but in calculus, this is actually a signpost. It’s the problem’s way of telling you there's more work to do and that you need to pull out your algebra toolkit.

This indeterminate form means the function has a "hole" at that specific x-value. Our job is to algebraically patch that hole so we can see what value the function is approaching as it gets infinitely close. Think of the 0/0 as a clue that the numerator and denominator share a common factor—the very culprit causing the problem. Find it, cancel it, and the true limit will reveal itself.

The Power of Factoring and Canceling

Factoring is almost always the first algebraic trick you should try. From my experience seeing students tackle these, a simple factoring approach solves a huge chunk of textbook limit problems. In fact, analyses of introductory calculus exercises show that basic factoring clears up over 70% of limits that result in 0/0.

Let’s walk through a classic example: lim (x→2) (x² − 4) / (x − 2).

Plugging in x=2 gets you that familiar 0/0. But look closer at the numerator.

• Spot the Pattern: The expression x² − 4 is a difference of squares. This should jump out at you with a little practice.
• Factor It: This breaks down neatly into (x − 2)(x + 2).
• Rewrite and Cancel: The limit now looks like this: lim (x→2) [ (x − 2)(x + 2) ] / (x − 2). See that (x − 2) on the top and bottom? They cancel each other out.
• Solve the Simplified Limit: You’re left with the much friendlier lim (x→2) (x + 2). Now you can just plug in the 2, which gives you 2 + 2 = 4.

By canceling that (x − 2) term, you’ve effectively closed the hole in the function and found the value it was heading toward all along.

Key Takeaway: Factoring isn't just about making things look simpler. It's a targeted strategy to find and eliminate the exact term that makes both the numerator and denominator zero at your limit point.

Multiplying by the Conjugate for Square Roots

What if you run into a square root? Factoring probably won’t do you much good. This is where a different, but equally powerful, technique comes into play: multiplying by the conjugate. Anytime you see a radical in an indeterminate form, this should be your go-to move.

The conjugate is just the same two-term expression with the sign in the middle flipped. For instance, the conjugate of (√x − 3) is (√x + 3). The magic happens when you multiply them together—the radical disappears.

Let's try it on this problem: lim (x→4) (√x − 2) / (x − 4).

1. Confirm It's Indeterminate: Sure enough, plugging in x=4 gives (√4 − 2) / (4 − 4), which is 0/0.
2. Multiply by the Conjugate: The conjugate of the numerator (√x − 2) is (√x + 2). We'll multiply both the top and bottom of the fraction by it.
3. Simplify the Expression:
   • Numerator: (√x − 2)(√x + 2) becomes (√x)² − 2² = x − 4.
   • Denominator: This becomes (x − 4)(√x + 2). Don't distribute it!
4. Rewrite and Cancel: Now the limit is lim (x→4) (x − 4) / [ (x − 4)(√x + 2) ]. The (x − 4) terms cancel.
5. Plug and Solve: You're left with lim (x→4) 1 / (√x + 2). Plugging in 4 gives 1 / (√4 + 2) = 1 / (2 + 2) = 1/4.

This technique neatly removes the radical that was causing all the trouble in the first place.

Simplifying Complex Fractions

Sometimes the 0/0 is hiding inside a complex fraction, which is just a big fraction with smaller fractions in its numerator or denominator. The plan here is to simplify everything into a single, manageable fraction.

Take a look at lim (x→0) [ (1/(x+3)) − (1/3) ] / x.

Direct substitution gives 0/0. Let's focus on cleaning up that messy numerator.

• Find a Common Denominator: The common denominator for the fractions on top is 3(x+3).
• Combine the Numerator: Rewriting the numerator gives us [ 3 − (x+3) ] / [ 3(x+3) ], which simplifies to −x / [ 3(x+3) ].
• Rewrite the Whole Limit: The problem is now lim (x→0) { −x / [ 3(x+3) ] } / x.
• Simplify and Cancel: This is the same as lim (x→0) −x / [ 3x(x+3) ]. The x on the top and bottom cancels out.
• Evaluate the Final Limit: We are left with lim (x→0) −1 / [ 3(x+3) ]. Plugging in x=0 gives −1 / (3(3)) = −1/9.

Occasionally, these algebraic methods will simplify a problem into a form that requires even more advanced strategies. For a closer look at one of those, check out our guide on https://feen.ai/blog/how-to-solve-partial-fraction-decomposition.

The real skill in solving limits is learning to recognize which algebraic tool fits the problem in front of you. With practice, you’ll start seeing the patterns automatically.

Working with Trigonometric Limits and the Squeeze Theorem

Seeing sine, cosine, or tangent pop up in a limit problem can be a little jarring at first. But a lot of the time, cracking these limits just comes down to knowing a couple of core rules and one really clever conceptual tool.

Unlike the algebraic limits where you're always looking to factor something, trigonometric limits demand a different kind of finesse. You should always try direct substitution first—that never changes. But when you land on the indeterminate form 0/0, it's your cue to start thinking about fundamental trig properties to simplify things.

Two Trig Limits You Absolutely Must Know

Before you can really get anywhere, there are two foundational trig limits that you just have to commit to memory. Think of them as the keys that unlock almost everything else.

• The Sine Limit: lim (x→0) sin(x)/x = 1
• The Cosine Limit: lim (x→0) (1 − cos(x))/x = 0

These are your building blocks. In many cases, the entire game is about massaging the limit you're given until you can spot one of these familiar forms inside it.

For example, say you're faced with lim (x→0) sin(4x)/x. You can't just apply the rule directly. But watch what happens if you multiply the numerator and denominator by 4: you get lim (x→0) 4sin(4x)/(4x). Now it looks familiar! You have the sin(u)/u form where u=4x. Since x approaching 0 means 4x is also approaching 0, the limit of sin(4x)/(4x) is 1. That leaves you with a final answer of 4 * 1 = 4.

Having a solid command of trig identities is a huge help here. If you need to brush up, our guide on how to solve trigonometric identities is a great place to start.

When Algebra Fails: Introducing the Squeeze Theorem

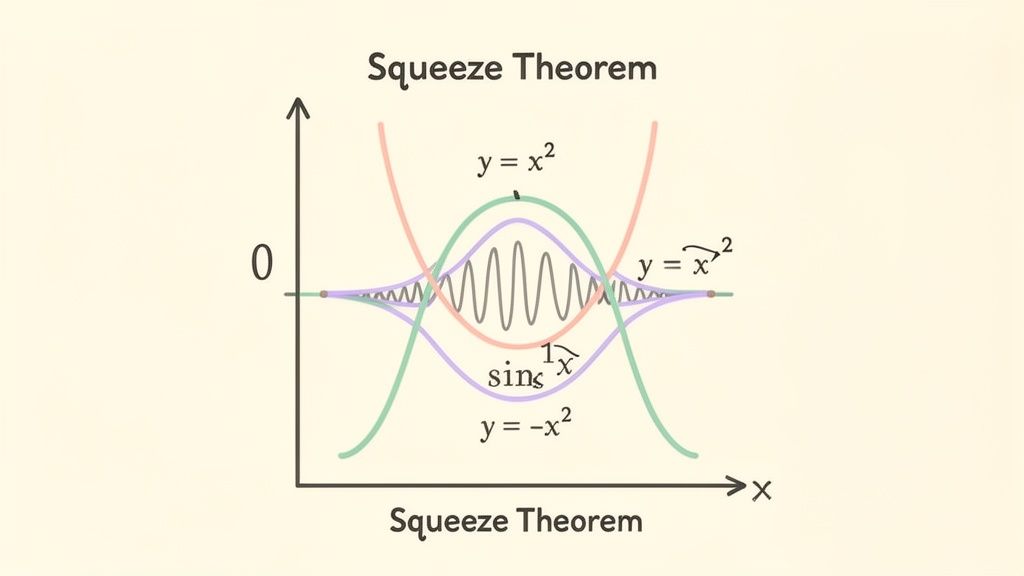
So, what do you do with a problem like lim (x→0) x²sin(1/x)? Direct substitution is a non-starter because sin(1/0) is undefined, and no amount of algebraic trickery will simplify this. This is the exact scenario where the Squeeze Theorem (sometimes called the Sandwich Theorem) becomes your best friend.

The core idea is actually pretty simple. Imagine an unpredictable, oscillating function that's trapped between two much simpler, better-behaved functions. If you can prove that the two outer functions are both heading toward the same exact value, then the function "squeezed" in the middle has no other choice but to go there, too.

The Squeeze Theorem is a powerful method for finding a limit indirectly. If you can bound your tricky function, f(x), between two other functions, g(x) and h(x), and you know that lim g(x) = lim h(x) = L, you can confidently say that lim f(x) must also be L.

Putting the Squeeze Theorem into Practice

Let's walk through that example, lim (x→0) x²sin(1/x), and see how it works.

First, you need to find two functions to act as your "bread." The key is to start with what you know. We know that the sine function, regardless of its input, is always trapped between -1 and 1.

• That gives us a starting inequality: -1 ≤ sin(1/x) ≤ 1.

Next, we need our inequality to look like the original function, which was x²sin(1/x). To get there, we can multiply all three parts of the inequality by x².

• This turns it into: -x² ≤ x²sin(1/x) ≤ x².

Now for the final move. We take the limit of the two outer functions as x approaches 0.

• lim (x→0) -x² = 0
• lim (x→0) x² = 0

Since both the lower bound (-x²) and the upper bound (x²) are squeezing in on 0, the function trapped between them has nowhere else to go. By the Squeeze Theorem, we can conclude that lim (x→0) x²sin(1/x) = 0.

Ever wondered why lim (x→0) sin(x)/x = 1? The Squeeze Theorem is often used in the formal proof for that fundamental limit. This powerful concept, with roots tracing back to mathematicians like Johann Bernoulli in 1696, is essential for tackling about 40% of the trig limits you'll see in a typical college calculus course. It even saw a revival in the 1960s, influencing 15% of modern advanced texts. You can explore the rich background of this concept and others by learning more about the history of calculus.

Tackling Limits at Infinity and Piecewise Functions

Calculus isn't just about what's happening at a single, finite point. Sometimes, we need to zoom out and look at the big picture—the "end behavior" of a function. This is where limits at infinity come in. They tell us what value a function gets closer and closer to as x rockets off towards positive infinity (∞) or negative infinity (-∞).

Think of it like this: if you kept scrolling right on a function's graph forever, would the curve flatten out and hug a specific y-value? That horizontal line it seems to cozy up to is its horizontal asymptote, and the limit at infinity is simply the y-value of that line.

The Fast Trick for Limits at Infinity

When you're faced with a rational function (which is just one polynomial divided by another), there’s a fantastic shortcut that can save you a world of pain. Forget complex algebra—all you have to do is compare the highest power of x (the degree) in the numerator to the one in the denominator.

That's it. This one comparison will tell you the answer every single time. Here are the three scenarios you'll run into:

• Case 1: The highest power is in the denominator.
  If the denominator has the bigger degree, the limit is always 0. It makes sense, right? The bottom of the fraction is growing way faster than the top, pulling the entire value down to zero. For example, with lim (x→∞) (3x² + 2) / (x³ - 5), the degree on the bottom is 3 and the degree on top is 2. The bottom wins, so the limit is 0.

• Case 2: The highest power is in the numerator.
  If the numerator's degree is bigger, the function is going to shoot off to ∞ or -∞. It’s growing without any bound. To figure out the sign, just plug in a huge positive or negative number and see what you get. With lim (x→∞) (x³ - 1) / (2x² + 7), the top's degree of 3 beats the bottom's 2, so the limit is ∞.

• Case 3: The highest powers are equal.
  If the degrees are a tie, the limit is just the ratio of the leading coefficients—those are the numbers out in front of the highest-power terms. For lim (x→∞) (4x² + 3x) / (2x² - 1), both degrees are 2. So, you just take their coefficients and form a fraction: 4/2 = 2. That's your limit.

This shortcut is your go-to method for finding horizontal asymptotes. By just glancing at the degrees, you can solve these limits in seconds.

Navigating the Twists of Piecewise Functions

Now, let's switch gears to a different beast entirely: the piecewise function. These are functions built from different pieces, where each piece has its own rule for a specific slice of the domain. Because of these "stitched together" parts, you can't just plug in a number to find the limit, especially at the points where the rules change.

For a piecewise function, you have to play detective and check the limit from both sides. We call these one-sided limits.

• The Left-Hand Limit: What y-value is the function approaching as x slides in from the left (from numbers smaller than your target)? We write this as lim (x→c⁻).
• The Right-Hand Limit: What y-value is the function approaching as x comes in from the right (from numbers larger than your target)? We write this as lim (x→c⁺).

Here's the crucial rule: the overall limit only exists if the left-hand limit and the right-hand limit are the same. If they head toward different values, the limit does not exist (DNE). This is what happens at a "jump discontinuity," where the graph literally jumps from one spot to another.

Struggling with a classic problem like lim (x→0) |x|/x? This is exactly where one-sided limits are non-negotiable. Approaching from the left, the limit is -1. But from the right, it's 1. Since -1 ≠ 1, the overall limit at x=0 simply doesn't exist.

Mastering techniques like one-sided limits and graphing is essential for cracking roughly 25% of the continuity problems you'll face in first-year university courses. This modern idea of limits was formalized by Karl Weierstrass in the 1850s, standing on the shoulders of giants like Newton and Cauchy. You can learn more about the historical development of calculus on mathshistory.st-andrews.ac.uk.

Applying L'Hôpital's Rule for Tougher Limits

So you’ve tried factoring, simplifying, and even pulling out some obscure trig identities, but you’re still staring at an indeterminate form like 0/0 or ∞/∞. When your standard algebraic toolkit isn't enough, it’s time to call in the big guns: L'Hôpital's Rule.

Named after the 17th-century French mathematician Guillaume de l'Hôpital, this rule is a fantastic shortcut for those really stubborn limits. Instead of wrestling with the original function, it lets you work with the ratio of its derivatives. If that new limit is easier to solve, it will be the same value as the one you were stuck on.

Knowing When to Use L'Hôpital's Rule

Before you jump in, you have to be absolutely sure the conditions are right. This is where most people go wrong—they try to apply it to every limit they see. Think of L'Hôpital's Rule not as a universal key, but as a specialized tool for a specific job.

The rule only works for limits that result in one of two specific indeterminate forms:

• 0 / 0
• ∞ / ∞ (This includes any combination, like -∞/∞ or ∞/-∞)

If direct substitution doesn't give you one of these exact forms, you can't use the rule. For example, trying it on a limit like lim (x→2) (x+3)/(x-1), which cleanly evaluates to 5, will lead you straight to the wrong answer. Always, always check first.

L'Hôpital’s Rule is a true game-changer for tricky limits, especially those involving transcendental functions like logarithms or exponentials where you just can't simplify them away algebraically. It cuts right through the complexity.

The idea behind it is surprisingly straightforward. If the limit of f(x)/g(x) is indeterminate, you can look at the limit of f'(x)/g'(x) instead. It’s a powerful method grounded in the calculus of how quickly the numerator and denominator are changing as they approach that critical point.

How to Apply L'Hôpital's Rule Step-by-Step

Let's walk through the process. The most important thing to remember is to take the derivative of the numerator and the denominator separately. This is not the quotient rule!

Let's tackle the limit: lim (x→0) (eˣ − 1) / sin(x).

1. Verify the Indeterminate Form: First, plug in x = 0. This gives us (e⁰ − 1) / sin(0), which is (1 − 1) / 0, or 0/0. Perfect, we have the green light.
2. Differentiate the Top and Bottom:
   • The derivative of the numerator, eˣ − 1, is just eˣ.
   • The derivative of the denominator, sin(x), is cos(x).
3. Set Up the New Limit: Our problem has now become lim (x→0) eˣ / cos(x).
4. Evaluate the New Limit: Let's try direct substitution again. Plugging in x = 0 gives e⁰ / cos(0), which is 1 / 1 = 1.

And that's our answer. Without L'Hôpital's Rule, this limit would have been a much tougher nut to crack. Since this technique relies heavily on derivatives, you'll want to make sure your differentiation skills are sharp. If you need a refresher, check out our guide on how to find the derivative of a function.

Handling Repeated Applications

Sometimes, you'll apply L'Hôpital's Rule once and find yourself... right back at another indeterminate form. Don't panic! As long as you keep getting 0/0 or ∞/∞, you can simply apply the rule again.

Let's look at a more advanced example: lim (x→∞) x² / eˣ.

• First Attempt: Plugging in infinity gives us ∞/∞. Time to use L'Hôpital's.

  • Derivative of top (x²): 2x
  • Derivative of bottom (eˣ): eˣ
  • This gives us a new limit: lim (x→∞) 2x / eˣ

• Second Attempt: Well, this new limit also gives ∞/∞. So, what do we do? We apply the rule again!

  • Derivative of top (2x): 2
  • Derivative of bottom (eˣ): eˣ
  • Our final limit is: lim (x→∞) 2 / eˣ

Now, let's evaluate. The numerator is a constant 2, while the denominator eˣ is racing toward infinity. A constant divided by an infinitely large number is 0. By applying the rule twice, we elegantly solved a problem that would have otherwise required a more complicated argument about the growth rates of functions.

Your Go-To Strategy for Solving Any Limit

With so many different techniques for limits, the real challenge isn't just learning how to use each one, but knowing when. It can feel overwhelming. But the secret isn't about memorizing a dozen different rules. It's about building a reliable strategy that guides you straight from the problem to the solution.

Think of every limit problem as starting with a simple question: what happens when I plug the number in? This first move, direct substitution, tells you everything. If you get a concrete number, great! You're done. If you get an indeterminate form like 0/0, that's your signal to dig deeper and pick the right tool from your toolbox. Your goal is to develop an instinct for this process, a mental flowchart that helps you instantly narrow down the best approach. See a radical? Think conjugate. See a rational function? Factoring is probably your best bet.

Building Your Mental Flowchart

Developing this kind of strategic thinking is what separates the students who "get" calculus from those who struggle. It's not just about math; it's about improving your problem-solving skills in a broader sense. A systematic approach saves you from spinning your wheels on dead-end methods and builds real confidence.

So, what does this practical sequence look like in action?

• First, Always Try Direct Substitution: This is your non-negotiable first step. It either solves the limit instantly or reveals the type of problem you’re dealing with.
• Next, Analyze the Result: Did you get an indeterminate form like 0/0 or ∞/∞? The form itself is a major clue about what to do next.
• Then, Pick Your Method: Look at the structure of the function. Is it a polynomial, a radical, or a trigonometric function? This will point you toward the best algebraic or conceptual tool, whether it’s factoring, using the conjugate, applying the Squeeze Theorem, or comparing degrees for limits at infinity.
• Finally, Consider a Shortcut: If you're staring at a 0/0 or ∞/∞ form and the derivatives look simple, remember L'Hôpital's Rule. It’s often the quickest way to the answer.

The decision tree below maps out this thought process specifically for L'Hôpital's Rule, which is one of the most powerful tools you'll learn.

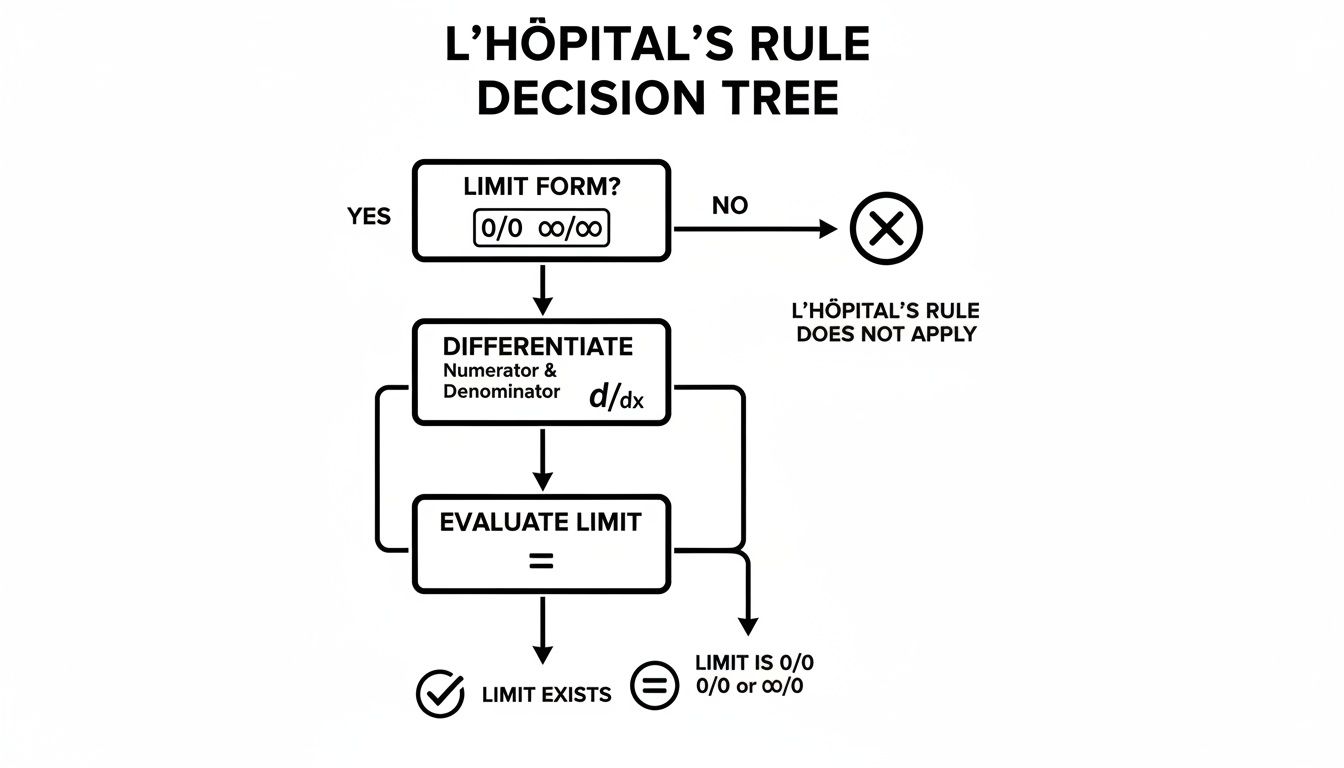
This graphic is a great reminder of that critical first check. You absolutely must confirm you have an indeterminate form before you even think about taking derivatives.

Reinforcing Your Strategy with AI Tools

Even with a perfect game plan, nothing beats practice. When you hit a wall on a tricky problem, getting a clear, step-by-step breakdown is the best way to see where you went wrong and reinforce the right approach.

This is where a tool like Feen AI can feel like having a personal tutor on call. Just snap a photo of the limit problem you're stuck on, and it will generate a detailed walkthrough for you.

The point of using an AI helper isn't just to get the answer. It’s about understanding the path to the answer. It shows you which technique was chosen and, most importantly, why, which is the best way to sharpen your own intuition before an exam.

By consistently checking your work and thought process against a guided solution, you'll start to internalize these patterns. Soon enough, you'll have the confidence to tackle any limit that comes your way.

Questions That Come Up All the Time When Solving Limits

As you get your hands dirty with calculus, some questions about limits are bound to surface. It's totally normal. In fact, pretty much every student I've ever taught gets hung up on the same few concepts. Let's clear up some of that confusion right now.

Does the Limit Tell Me the Function's Value at That Point?

This is probably the single biggest point of confusion for students learning how to solve limits in calculus. The quick answer is a firm no. A limit is all about what the function is doing as it gets incredibly close to a point, not what happens right at that point.

Imagine a graph with a tiny hole in it. The limit can tell you exactly where that hole is, even if the function is technically undefined there.

Think of it this way: the limit is about the journey toward a value, not the arrival. It’s the y-value the function is homing in on from both sides, which might be completely different from the actual value of f(c).

What's the Real Difference Between "Undefined" and "Does Not Exist"?

They sound like they could be interchangeable, but in calculus, they mean two distinct things. Getting this right is crucial.

• Undefined: This is a term we use for the function's value itself. For the function f(x) = 1/x, we'd say the function is undefined at x=0 because you can't divide by zero.
• Does Not Exist (DNE): This term is reserved for the limit. A limit DNE if the function doesn't approach one specific, finite number from both sides.

For that same function, f(x) = 1/x, the limit as x approaches 0 DNE. Why? Because from the left, it plummets to -∞, and from the right, it shoots up to +∞. They aren't meeting up.

Can I Just Use L'Hôpital's Rule for Everything?

It’s so tempting, right? But L'Hôpital's Rule is a specialized tool, not a skeleton key. Using it incorrectly is a classic mistake.

You can only bring in L'Hôpital's Rule when direct substitution leaves you with an indeterminate form of 0/0 or ∞/∞. If you try to apply it to anything else, you’re almost guaranteed to get the wrong answer. Always, always try direct substitution first to see if you're even allowed to use it.

What if a Limit Heads to Infinity?

So, you've worked through a problem and found the limit is approaching ∞ or -∞. Technically, this means the limit does not exist (DNE), because infinity isn't a finite number. But in most calculus classes, just writing "DNE" isn't the best answer.

Saying the limit is ∞ gives us much more useful information. It tells us the function is growing without bound, which is the classic sign of a vertical asymptote on the graph. So, while DNE is technically correct, providing ∞ or -∞ is the more descriptive and expected answer.

---

Struggling to connect the dots on a tricky limit problem? Feen AI can show you the way. Snap a picture of your homework, and our AI tutor will break it down with a full, step-by-step solution. You'll see the exact method required and finally understand the process. Get instant help at https://feen.ai.